牛顿法及牛顿法求解优化问题

牛顿法

1. 由来和基本思想

牛顿法也叫牛顿迭代法和牛顿-拉夫森法
1. 牛顿迭代法：因为牛顿法的是通过迭代来实现的，每次运算都让结果比之前好一点。哪怕只好一点点，在很多次迭代之后也可以得到一个很好的结果甚至最优或期望的结果。迭代就是我们常说的积土成山，积善成德。
2. 牛顿-拉夫森法： 牛顿和拉夫森两个人都提出了牛顿法，但拉夫森比较地调而且鲜为人知。

2. 一句话描述牛顿法

牛顿法就是通过使原方程泰勒展开的一阶近似等于零不断获得更好的结果的求解方程零点的方法。

3. 详细解释牛顿法

• 牛顿法是求解方程零点的方法
• 牛顿法利用泰勒展开的一阶近似的零点获得更接近真实零点的点
• 牛顿法通过迭代的方法不断的获得更好的解来求得最好的解

1. 泰勒展开

$f(x)=f(x_0)+f^\prime(x_0)(x-x_0)+\frac{1}{2}f^{\prime\prime}(x-x_0)(x-x_0)^2+\dots + \frac{1}{n!}f^{(n)}(x-x_0)(x-x_0)^n + o(x-x_0)^n$

2. 一阶近似
$f(x)=f(x_0)+f^\prime(x_0)(x-x_0)$

3. 求出更接近零点的点
$f(x_0)+f^\prime(x_0)(x-x_0)=0$
$\implies x_1=x_0-\frac{f(x_0)}{f^\prime(x_0)}$

4. 迭代求出零点
$x_{k+1}=x_k-\frac{f(x_k)}{f^\prime(x_k)}$

5. 终止条件(迭代算法一定要有终止条件)
$x_k< stopping\_criterion$

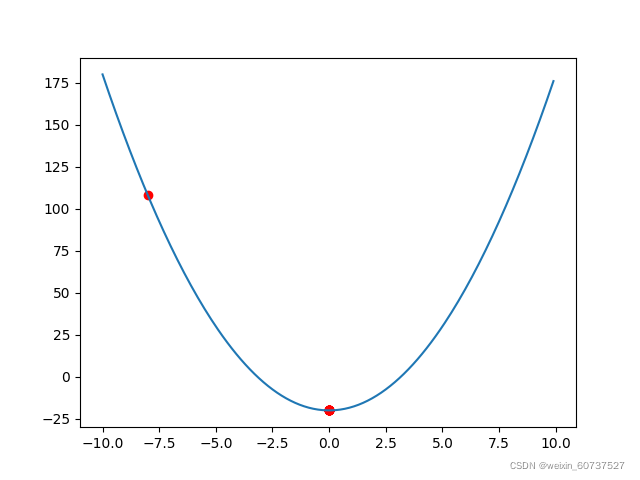
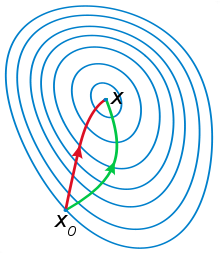
4.图像直观解释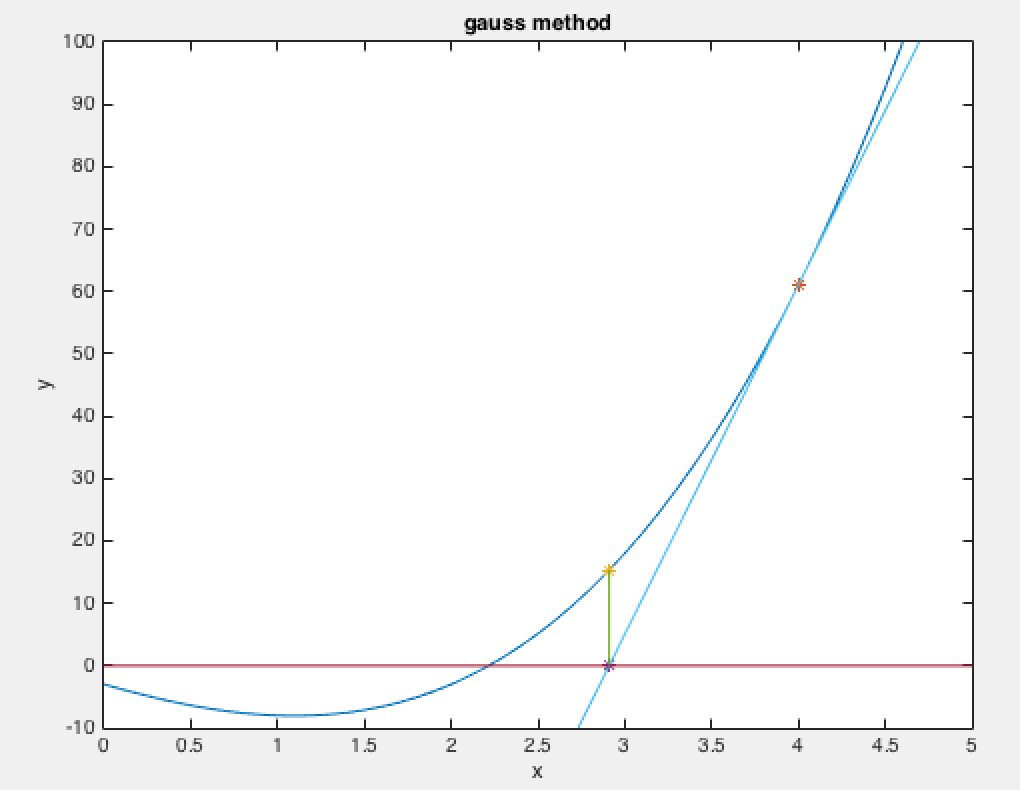

图中，橙色的雪花点是前一次的位置，一次牛顿迭代后，变化到黄色的雪花点。
由图可知，每一次迭代都可以是x更靠近真实的零点。

5.为什么用一阶近似而不用二阶近似或者更高阶近似？

因为，1. 二阶及以上的方程不一定有解，而且求解过程比一阶近似更复杂，尤其是三节以上的近似。如果求解不复杂，我们就不用牛顿法求解了。2. 一阶近似已经可以达到我们的目的。
至此，牛顿法介绍完毕。

牛顿法求解优化问题

优化问题

一般优化问题可以描述为：
$min_x \quad f_0(x)$
$f_i(x)<=0 \quad i=1,2 \dots n$
$h_j(x)=0\quad j=1,2 \dots m$
如果m,n都等于0，则称之为无约束优化问题，牛顿法可用于求解无约束优化问题
如果$f_0(x)$是凸函数，则为凸优化问题，牛顿法可以求解凸优化问题，如果$f_0(x)$非凸，则不一定能获得最优解，能否获得取决于初始点的选取

牛顿问题求解优化问题

优化问题的最优解一般出现在函数的极值点上，也就$f^\prime(x)=0$的解，所以，牛顿法求解优化问题即求解$f^\prime(x)$的零点。至于求零点，前面所说的方法就可以解决了。

求解具体步骤

1. 泰勒展开

$f(x)=f(x_0)+f^\prime(x_0)(x-x_0)+\frac{1}{2}f^{\prime\prime}(x-x_0)(x-x_0)^2+\dots + \frac{1}{n!}f^{(n)}(x-x_0)(x-x_0)^n + o(x-x_0)^n$

2. 二阶近似（因为二阶近似的导数为原方程导数的一阶近似）
$f(x)=f(x_0)+f^\prime(x_0)(x-x_0)+\frac{1}{2}f^{\prime\prime}(x-x_0)(x-x_0)^2$

3. 求导
$f^\prime(x)=f^\prime(x_0)+f^{\prime\prime}(x_0)(x-x_0)$

4. 求出更接近零点的点（后面的和牛顿法相同）
$f^\prime(x_0)+f^{\prime\prime}(x_0)(x-x_0)=0$
$\implies x_1=x_0-\frac{f^{\prime}(x_0)}{f^{\prime\prime}(x_0)}$

5. 终止条件(迭代算法一定要有终止条件)

6. $f(x_k)为最小值$