牛顿法一般指牛顿迭代法,也叫做牛顿-拉夫逊(拉弗森)方法(Newton-Raphson method),其最初的作用是用来求解函数的零点,但是也可以像梯度下降方法一样,以迭代的形式来求函数的极值。而事实上,牛顿法求零点和极值的思想是一样的,因为函数的极值点对应就是函数的导数的零点(但导数零点有时可能是函数的极大、极小或驻点)。所以牛顿法求函数极小值还是有许多的问题的。
(一)牛顿法求零点。
(1)基本原理
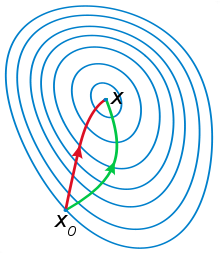
牛顿法的思想就是在函数曲线上初始一个点,做该点的切线与x轴交于x0,然后再过(x0,f(x0))点作函数切线,切线与x轴交下一个点x0......依次迭代,最终x便趋近于零点。公式的推导需要泰勒展开等内容,也并不复杂,兔兔把结论直接写在下面了:
初始的x0可以随机初始,最终可以收敛到零点的。
(2)算法实现
兔兔这里以函数在区间[10,10]的零点求解为例。
import numpy as np
import matplotlib.pyplot as plt
def f(x):'''待求解函数'''return 2*x**2-20
def df(x):'''函数导数'''return 4*x
x=np.arange(-10,10,0.1)
y=f(x)
x0=-8 #初始x0
xt=[x0] #记录每次迭代的点x
for i in range(20):x0=x0-f(x0)/df(x0)xt.append(x0)
xt=np.array(xt)
plt.plot(x,y)
plt.scatter(xt,f(xt),color='red')
plt.show()运行结果如下:
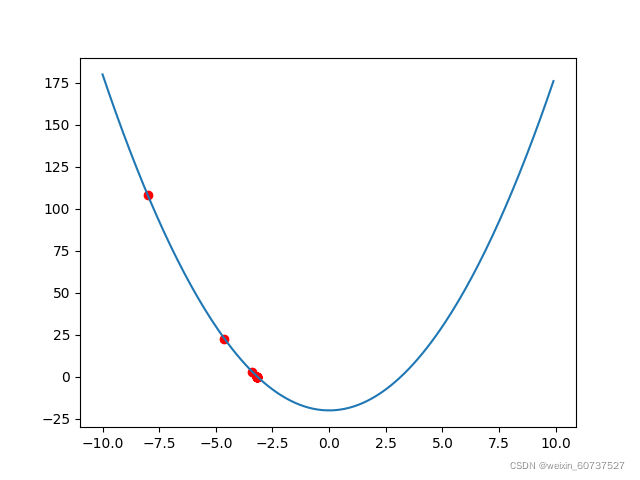
我们发现,结果可以很快收敛到零点,最终的零点计算得-3.16227766,与实际值很接近了。而且我们还发现,这个函数其实是有两个零点的,而该方法最终只收敛得到一个零点,所以最终结果是严重依赖于初始值x0的选取,如果x0在右侧选取,最终得到的结果就是
。
(二)牛顿法求函数极小值
(1)基本原理
实质上,兔兔前面提到了,我们最终求的是函数的导数的零点,那么就不一定是极小值,也可能是极大值或驻点。但是在实际问题中,一方面,我们遇到的函数(如构造损失函数)都是类似于抛物线形状,也就是只有下限却没有上限,另一方面,我们需要求解函数的极小值点,所以在这种情况下可以用牛顿法去求极小值点或优化参数等。但是,由于牛顿法迭代最终结果严重依赖初始值的选取,所以该方法往往会收敛到局部最优(或是极小值点),而不是全局最优(或是最大值点)。这些问题也只能用其它的方法来改进了。
回到(一)中(1)的迭代公式,我们这里是求的零点,所以可以把
替换公式中的
,最终的迭代公式为:
(2)算法实现
兔兔这里还是以上一个函数为例。
import numpy as np
import matplotlib.pyplot as plt
def f(x):'''待求解函数'''return 2*x**2-20
def df(x):'''函数导数'''return 4*x
def ddf(x):'''函数二阶导数'''return 4
x=np.arange(-10,10,0.1)
y=f(x)
x0=-8 #初始x0
xt=[x0] #记录每次迭代的点x
for i in range(20):x0=x0-df(x0)/ddf(x0)xt.append(x0)
xt=np.array(xt)
plt.plot(x,y)
plt.scatter(xt,f(xt),color='red')
plt.show()兔兔在(一)的基础上稍稍改动了一下代码。运行结果如下:
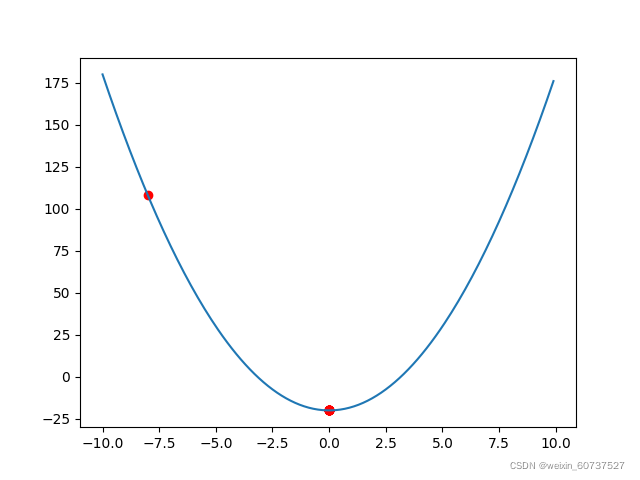
我们发现,基本迭代一次就达到极小值点了。
但事实上,在很多时候是很难达到这样的效果的。比如对于sin(x)这样的函数,它可能就随着初始值的不同而可能达到极大或极小值点,有时弄不好会导致二阶导数值为0,从而报错,导致程序无法进行。
(三)总结
牛顿法作为一种迭代方法,虽然有着收敛速度快、算法简便等优点,但是也有很多的问题。所以之后才会有牛顿下山法、拟牛顿法(或共轭方法发)系列、阻尼牛顿法等方法的出现,而且还有多元函数牛顿法等。本文的牛顿法所解决的仅限于一元函数,关于其它的方法兔兔会逐步深入讲解的。