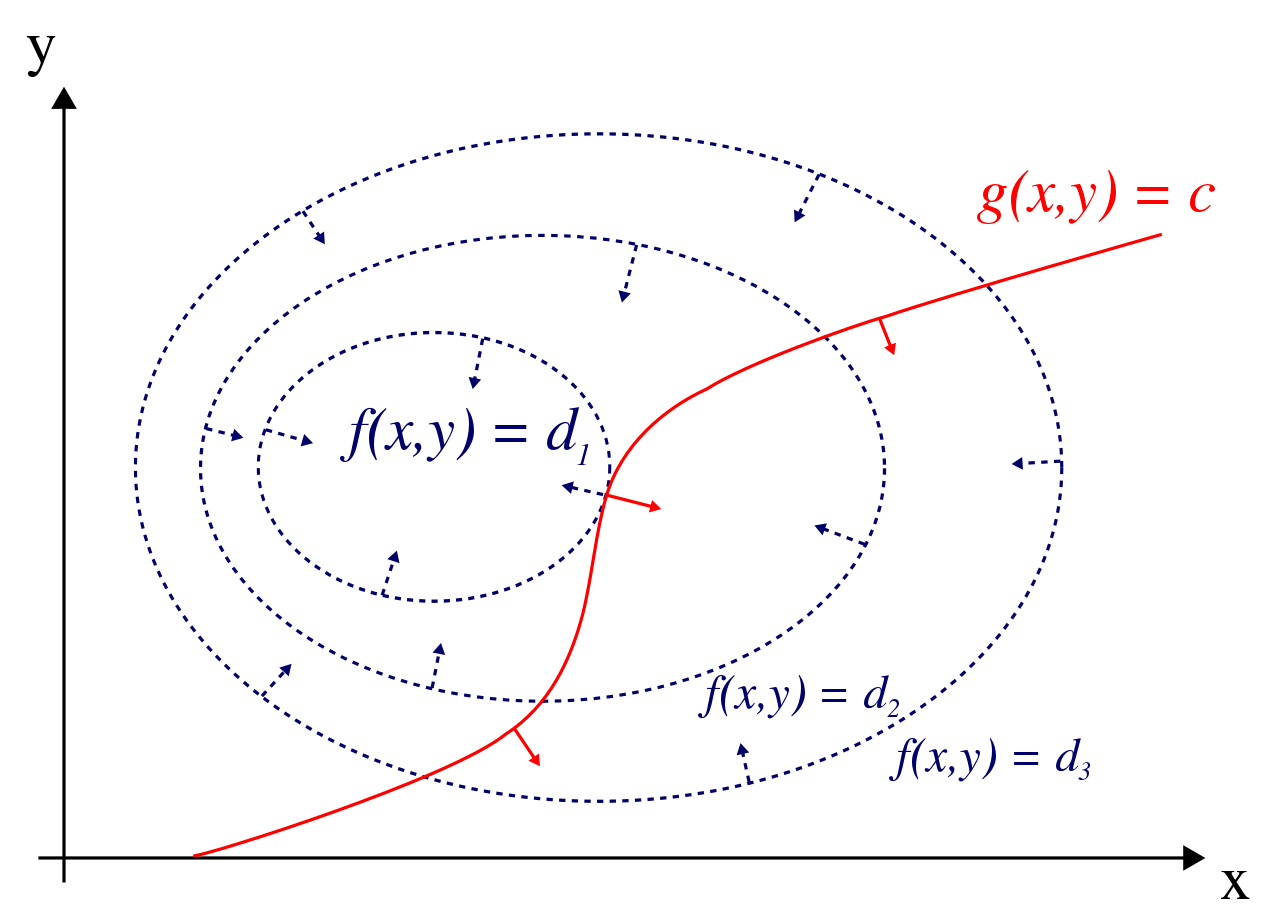
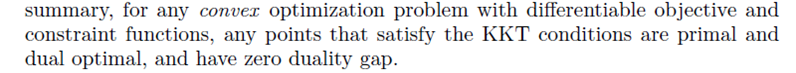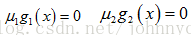/*常数变易法* 打印金字塔*          **         * **        * * **       * * * **      * * * * **/
public class A {public static void main(String[] args) {//常数变易法，演变过程System.out.println("         *");//第一行System.out.println("        * *");//第二行//System.out.println("       * * *");//第三行for(int i=0;i<7;i++) System.out.print(" ");for(int i=0;i<3;i++) System.out.print("* ");System.out.println();//System.out.println("      * * * *");//第四行for(int i=0;i<6;i++) System.out.print(" ");for(int i=0;i<4;i++) System.out.print("* ");System.out.println();//System.out.println("     * * * * *");//第五行for(int i=0;i<5;i++) System.out.print(" ");for(int i=0;i<5;i++) System.out.print("* ");System.out.println();System.out.println("--------------------------------------");//总共要打印5行*
//      for(int k=0;k<5;k++){
//          for(int i=0;i<?;i++) System.out.print(" ");
//          for(int i=0;i<??;i++) System.out.print("* ");
//          System.out.println();
//      }
//      k: 0 1 2 3 4 
//      i: 9 8 7 6 5   i=9-k 替换掉第一个?
//      j: 1 2 3 4 5   j=k+1 替换掉第二个??for(int k=0;k<5;k++){for(int i=0;i<9-k;i++) System.out.print(" ");for(int i=0;i<k+1;i++) System.out.print("* ");System.out.println();}}
}

结果：