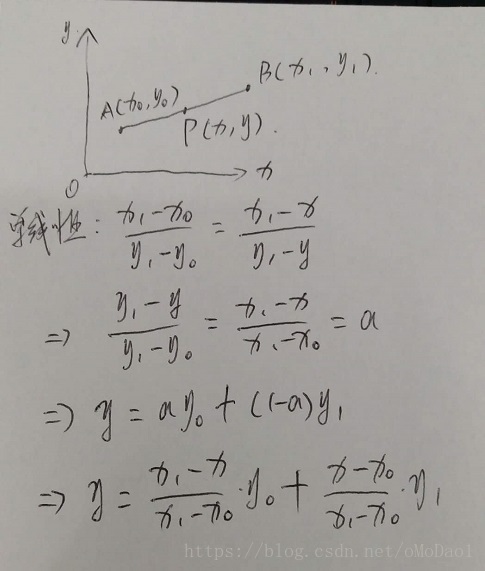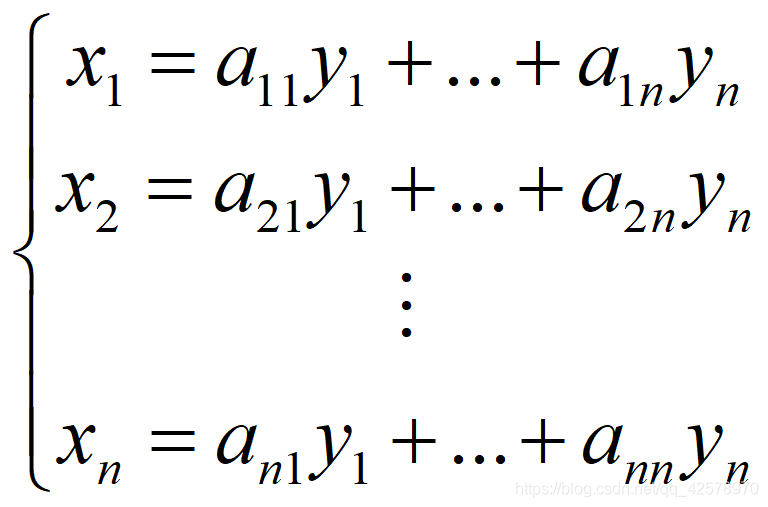转载自https://lianera.github.io/post/2018/fast-trilinear-interpolation/
快速三线性插值
最近需要对一个体素进行插值，并且应用到一张大图像上。这个本来用三线性插值很容易就实现了，但是体素的尺寸很小，长宽高大概20x15x10的大小，图像的尺寸非常大，差不多是4000x3000，等我实现完普通的三线性插值后，发现算法速度实在太慢，单是这一项三线性插值耗费的时间就占了总程序的一半多。其实如果能够用GPU，利用OpenGL里面的3d texture是最方便，也最快的，但是图像从内存传送到GPU需要耗费一定时间，并且很多情况下没法用GPU。所以只能推导一下，在体素上事先就进行预计算，然后再用参数应用到大图像上。

原理
借用一张常用的三线性插值示意图

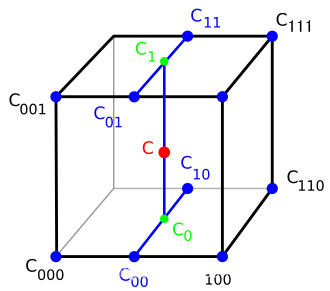
三线性插值实际上可以通过7次线性插值实现。首先假定使用左手坐标系，z轴朝上，在x方向上对四条棱边进行四次插值，得到每条边上的四个点的值c00,c01,c10,c11，然后在y方向上对四个点进行插值，得到两条线段以及中间的两个点的值c0,c1，然后在z方向上插值，得到最终的c点的值。

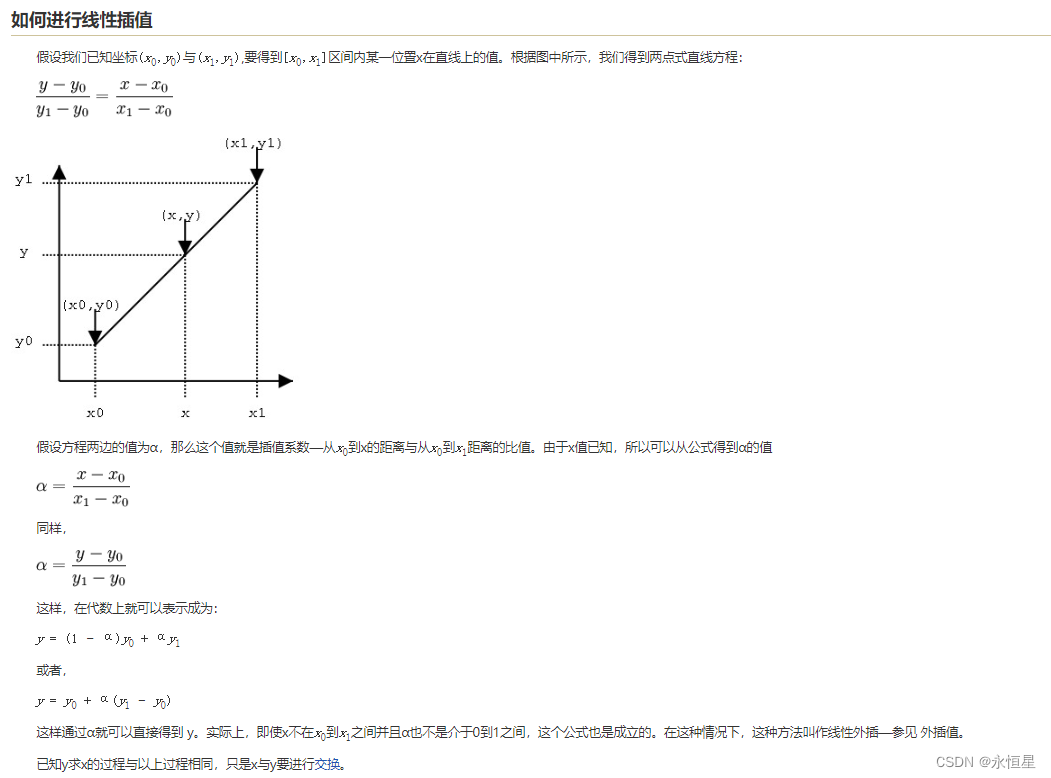
我们知道，对于线性插值来说，其公式为：

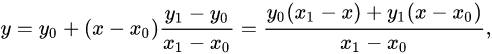
其中包括四次加减运算，三次乘除运算，因此总的来说，进行一次三线性插值，运算总数为28次加减运算，21次乘除运算，并且往体素中寻找位置并且取值还要花费大量的运算，对于大图像来说，总的运算耗费的时间非常大。

假定立方体原点为(x0,y0,z0)，离原点最远的点为(x1,y1,z1)，立方体的每个顶点的值在体素中是知道的。值得注意的是，虽然现在计算的坐标位置实际上是插值时的位置，但是实际上插值只与待求点(x,y,z)与(x0,y0,z0)和(x1,y1,z1)的相对位置比有关，不过为了后续插值的方便，建议首先将点映射到目标坐标上，这样在插值的时候就不需要再进行坐标映射。首先对x方向上插值，得到yz平面上四个点的值分别为f1,f2,f3,f4：


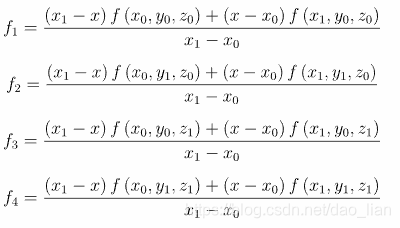
注意一下，这里面隐含了x1和x0不能相等，如果两者相等，则f1=f(x0,y0,z0)=f(x1,y0,z0)恒成立，所以直接设置成x1=1,x0=0，再用上述公式即可。注意到，这里面的矩阵是不包含未知数的，这是个常数矩阵。这样一来，我们可以事先在体素上计算好矩阵，最后再应用到图像上就好了。当然我们这还只是一次线性插值，现在继续插值。我们令上面式子f1,f2,f3,f4中右侧矩阵分别为M1,M2,M3,M4，因为是常数矩阵，我们将他们用常数a,b替换。同样利用线性插值方法，现在在y轴方向上插值，计算1,2插值的点5,以及3,4插值的点6



实现
预计算参数的实现直接按照上面的常数参数计算即可，因为预计算是在小的体素上面实现的，所以不用太担心速度。

c++
/* precompute trilinear coefficients
* v: f(x0,y0,z0), f(x1,y0,z0), f(x0,y1,z0), f(x1,y1,z0)
*    f(x0,y0,z1), f(x1,y0,z1), f(x0,y1,z1), f(x1,y1,z1)
*/
template <typename T>
array<T,8> PreComp(float x0, float y0, float z0, float x1, float y1, float z1, const array<T,8>& v)
{const float epsilon = 10e-6f;if (x1 - x0 < epsilon) { x1 = 1.f; x0 = 0.f; }if (y1 - y0 < epsilon) { y1 = 1.f; y0 = 0.f; }if (z1 - z0 < epsilon) { z1 = 1.f; z0 = 0.f; }float deno = (x1 - x0)*(y1 - y0)*(z1 - z0);float nume = 1.f / deno;T a1 = x1 * v[0] - x0 * v[1];T a2 = x1 * v[2] - x0 * v[3];T a3 = x1 * v[4] - x0 * v[5];T a4 = x1 * v[6] - x0 * v[7];T b1 = v[1] - v[0];T b2 = v[3] - v[2];T b3 = v[5] - v[4];T b4 = v[7] - v[6];T c5 = y1 * a1 - y0 * a2;T c6 = y1 * a3 - y0 * a4;T d5 = a2 - a1;T d6 = a4 - a3;T e5 = y1 * b1 - y0 * b2;T e6 = y1 * b3 - y0 * b4;T f5 = b2 - b1;T f6 = b4 - b3;T h1 = z1 * c5 - z0 * c6;T h2 = z1 * d5 - z0 * d6;T h3 = z1 * e5 - z0 * e6;T h4 = z1 * f5 - z0 * f6;T h5 = c6 - c5;T h6 = d6 - d5;T h7 = e6 - e5;T h8 = f6 - f5;array<T, 8> h = {h1*nume, h2*nume, h3*nume, h4*nume, h5*nume, h6*nume, h7*nume, h8*nume};return h;
}

而插值的时候，速度就是比较重要的了，因为大体素与小体素对应的时候，block是共享参数的，并且即使是变量x,y,z也可以预先计算一部分，不用每个cell都计算。具体来说，插值的时候直接应用f7的计算公式即可：

T val = zf * (yf*(h[7] * xf + h[5]) + h[6] * xf + h[4])+ yf * (h[3] * xf + h[1]) + h[2] * xf + h[0];

结果
对一个20x20x20的小体素进行预计算，然后用上述的三线性插值放大5倍，形成一个100x100x100大小的体素。

原体素


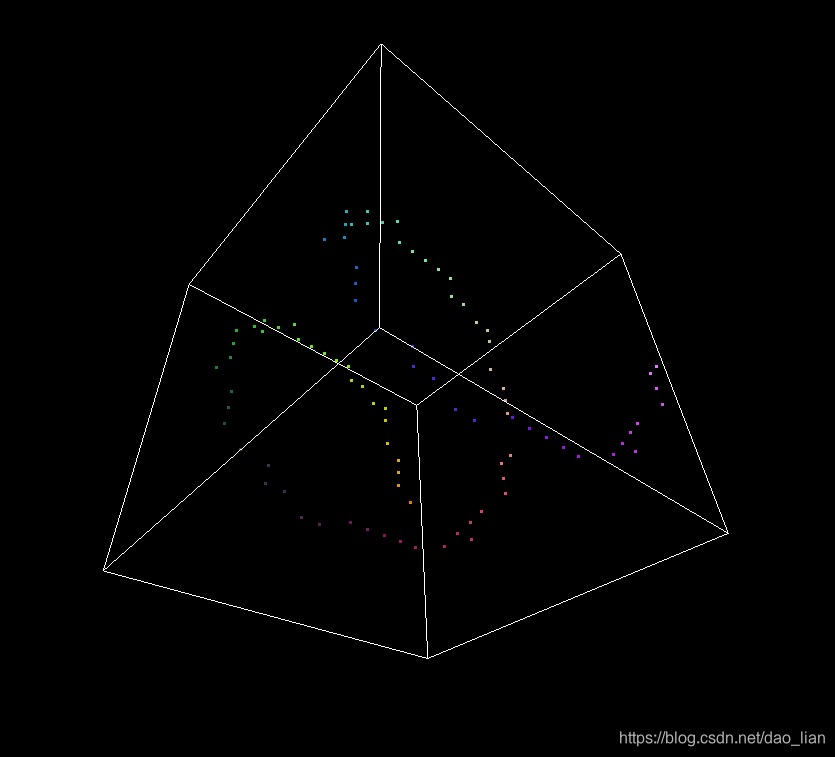
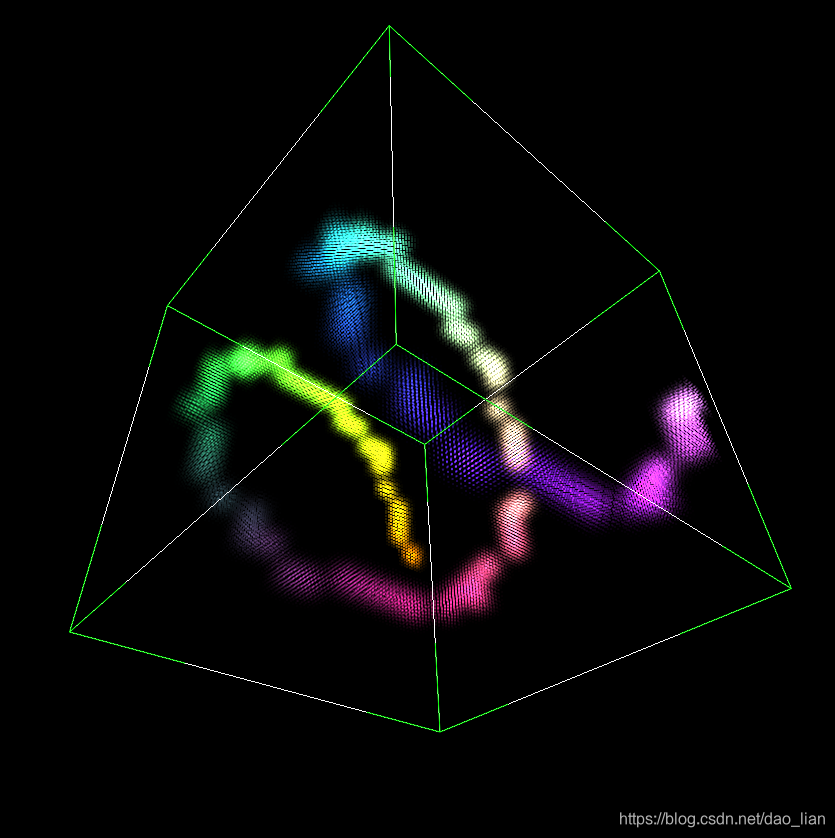
完整代码：https://lianera.github.io/post/2018/fast-trilinear-interpolation/main.cpp