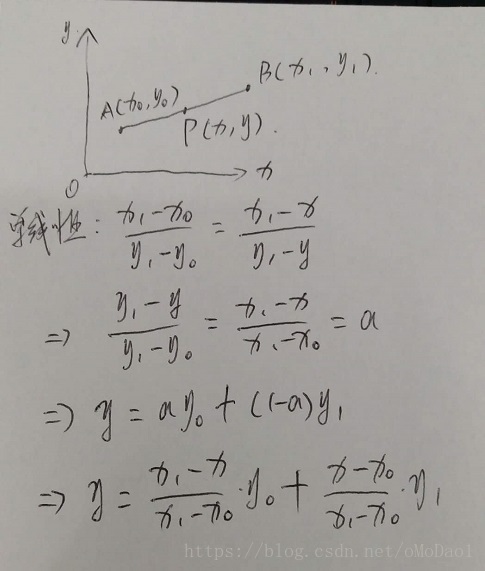前言

插值计算普遍存在于图像处理中,最近在做畸变优化时,看了一些资料中提到了插值&双线性插值,开始没明白,觉得一定很难,直接跳过,到最终写代码时,又不得不使用.于是就这里对这个功能进行学习,记录,并使用vs2017进行实际验证,验证后发现这个原理其实并不复杂.

插值

$插值的数学定义:给定n个已知离散数据点(x_k,y_k),k=1,2,...,n.对于x \neq x_k,k=1,2,...,n,求x所对应的y的值称为内插。$
$f(x)为定义在区间 [a,b]上的函数.x_1,x_2,x_3...x_n,为[a,b]上n个互不相同的点， G为给定的某一函数类。$
$若G上有函数g(x)满足:g(x_i)=f(x_i),k=1,2,...n,则称g(x)为f(x)关于节点x_1,x_2,x_3...x_n,在 G上的插值函数.$
(这里听起来就不太好理解,暂时心里有点印象即可,后面会对这个进行举例说明).
在数值分析的数学领域,插值是在已知数据点的离散集合的范围内构建新的数据点的方法.例如在图片放大时,如果直接放大2倍,那么就会出现有很多像素点为空的情况,这时候就需要对这些空值进行填充,插值广泛的引用到图像处理当中.

线性插值

线性插值介绍

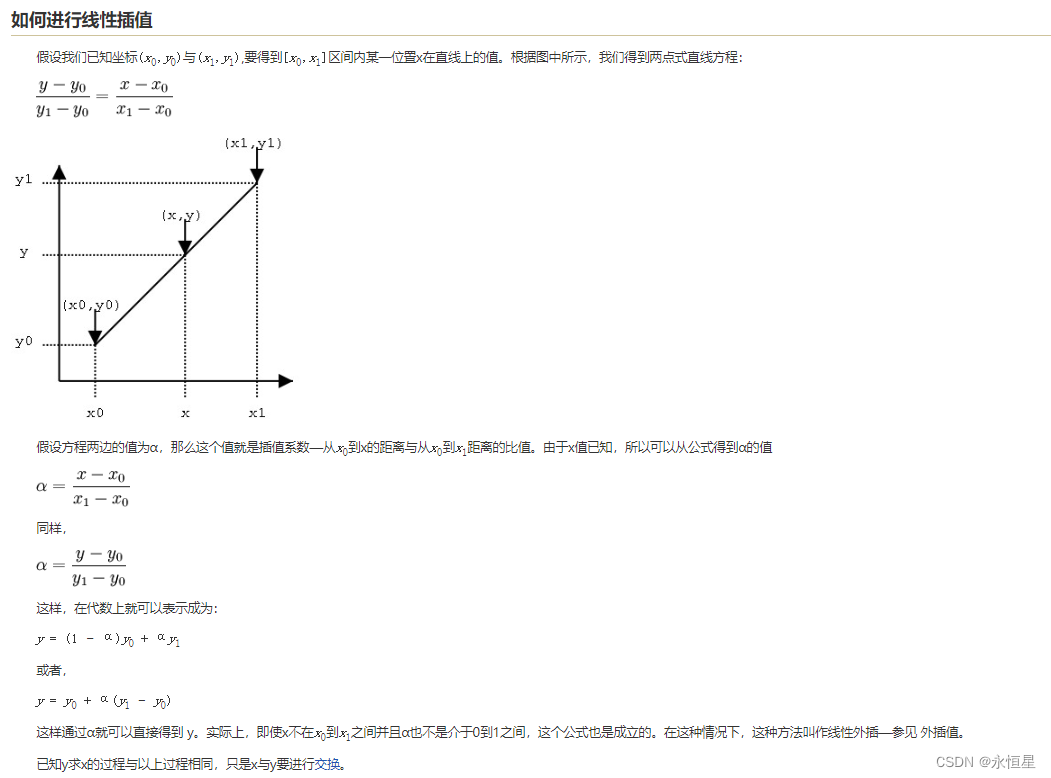
$直线L上有已知点A(x_0,y_0),B(x_1,y_1),C在直线L上,已知C的x坐标,求y坐标,手动画了一个示意图:$
这里写图片描述
$tan∠BAD=\frac {|CE|}{|AE|}=\frac {|BD|}{|AD|}\Rightarrow\frac {y-y_0}{x-x_0}=\frac {y_1-y_0}{x_1-x_0},等式整理后$ :
$y=\frac {x_1-x}{x_1-x_0}y_0+\frac {x-x_0}{x_1-x_0}y1 --------------------------公式①$
$这里将y_0和y_1的系数看成k1,k2,y就变成了y_0和y_1的加权平均数:$
$y=k_1y_0+k_2y_1$
同时可以看出C离A,B哪个点越近,哪个点的权重系数k值就越大,最终y值受它的影响也越大.

线性插值验证

假设直线L:y=2x+1,点A(1,3),点B(3,7)在直线L上.若有一点C,X轴坐标为2,求点C的坐标.
这里验证较为简单,将数据带入公式①中可得C为(2,5),此点满足y=2x+1.

双线性插值&多线性插值

双线性插值介绍

双线性插值是对线性插值的扩展,主要用于2D图像处理中,”双”是指在两个方向上进行分别进行线性插值,关键思想是先在一个方向上进行线性插值,然后在另一个方向上进行线性插值(这2个方向进行线性插值的顺序可以颠倒).这里直接引用维基百科中的图片,然后对算法描述
这里写图片描述
$此时,我们已知四个点Q_{11}(x_1,y_1),Q_{21}(x_2,y_1),Q_{12}(x_1,y_2),Q_{22}(x_2,y_2),求点P(x,y)处的f(x,y)的值.$
我们首先在x方向进行两次线性插值(步骤与上节”线性插值介绍”一致),得出结果:
$f(x,y1)\approx\frac {x_2-x}{x_2-x_1}f(Q_{11})+\frac {x-x_1}{x_2-x_1}f(Q_{21})$
$f(x,y2)\approx\frac {x_2-x}{x_2-x_1}f(Q_{12})+\frac {x-x_1}{x_2-x_1}f(Q_{22})$
我们继续在y方向插值以获得所需的估计：
这里写图片描述
请注意，如果首先沿着y方向，然后沿x方向进行插值，我们将得到相同的结果。

这里总共进行了2次X轴的线性插值和1次Y轴的线性插值.

双线性插值验证

这里以维基百科上的图片,添加了一些辅助信息:
这里写图片描述
如上图中所示,已知:
$Q_{11}(14,21)像素值为162$
$Q_{21}(15,21)像素值为95$
$Q_{12}(14,20)像素值为91$
$Q_{22}(15,20)像素值为210$
$求:P(14.5,20.2)的像素值是多少?$
步骤是这样的:

处理X轴方向的线性插值,这里包括两个插值过程.
- $第一个是Q_{11}和Q_{21}组成的直线上做一次线性插值,得出P_{11}(14.5,21):$
  $P_{11}(14.5,21)=\frac {15-14.5}{15-14}\times162+\frac {14.5-14}{15-14}\times95=128.5$
- $第二个是Q_{12}和Q_{22}组成的直线上做一次线性插值,得出P_{12}(14.5,20):$
  $P_{12}(14.5,20)=\frac {15-14.5}{15-14}\times91+\frac {14.5-14}{15-14}\times210=150.5$
$在X轴上做插值的基础上,处理Y轴方向的线性插值,即在P_{11}(14.5,21)和P_{12}(14.5,20)做一次线性插值,得出P(14.5,20.2):$
$P(14.5,20.2)=\frac {21-20.2}{21-20}\times150.5+\frac {20.2-20}{21-20}\times128.5=146.1$

上面这个双线性计算的步骤,建议手动算一遍,确保理解了之前的线性插值,以及双线性插值,对后面代码实例中图片的处理会有很大的帮助,同时有利于理解三线性插值,因为双线性插值相对于线性插值上的步骤与三线性插值相对于双线性插值的意义是一样的.

插值的使用

我们对原图进行放大两倍的操作,以不使用插值算法和使用双线性插值算法进行比较,来说明插值在处理图像时的优势.

原理说明

图片由MxN个像素组成,这里将原图分割成若干个3x3方格,对其进行扩大两倍的操作进行说明:
这里写图片描述
其中’●’表示扩大前的像素点,’X’为扩大后需要填充的像素点,无线性插值的情况,这里填充像素为0（即黑色）,线性插值的情况类似与本文上小节中介绍”双线性插值验证”那样,即 $Q_{11},Q_{21},Q_{12},Q_{22}$ 通过线性插值计算出,P1,P2,P3,P4的像素,在通过双线性插值计算出P5点的像素,其他四个区域同理,然后将这种3x3方格推广到整个图片区域(MxN)中,完成线性插值的工作.

代码实现

这里使用Visual Studio 2017工具,基于MFC,制作了一个工程,有需要的可以到这里下载使用,主要代码如下:

...(省略无关部分)//加载并显示原图CPaintDC paint_dc(this);CDC dcMem;BITMAP bit_map;dcMem.CreateCompatibleDC(&paint_dc);origin_bitmap.LoadBitmap(IDB_BITMAP1);origin_bitmap.GetBitmap(&bit_map);CBitmap *pbmpOld = dcMem.SelectObject(&origin_bitmap);paint_dc.StretchBlt(10, 10, bit_map.bmWidth, bit_map.bmHeight, &dcMem, 0, 0, bit_map.bmWidth, bit_map.bmHeight, SRCCOPY);dcMem.SelectObject(pbmpOld);dcMem.DeleteDC();CDialogEx::OnPaint();CImage origin_image;HBITMAP hbmp = (HBITMAP)origin_bitmap.GetSafeHandle();origin_image.Attach(hbmp);//获取图片宽和高int width = origin_image.GetWidth();int height = origin_image.GetHeight();//每张图片显示的间隔.int picture_interval = 50;CDC *pDC = GetDC();        COLORREF color;COLORREF clr;int ***origin_pixel;origin_pixel = new int **[RGB_TYPES];for( int i=0; i<RGB_TYPES; i++ ){origin_pixel[i] = new int *[width];for( int j=0; j<width; j++ ){origin_pixel[i][j] = new int [height];}}//获取原图像的所有像素for (int i = 0; i<width; i++){for (int j = 0; j<height; j++){color = origin_image.GetPixel(i, j);origin_pixel[RGB_R][i][j] = GetRValue(color);origin_pixel[RGB_G][i][j] = GetGValue(color);origin_pixel[RGB_B][i][j] = GetBValue(color);}}int ***large_2_pixel;large_2_pixel = new int **[RGB_TYPES];for (int i = 0; i<3; i++){large_2_pixel[i] = new int *[width*2];for (int j = 0; j<width*2; j++){large_2_pixel[i][j] = new int[height * 2];}}for(int index = 0; index < RGB_TYPES;index++){for (int i = 0; i<width*2; i++){for (int j = 0; j<height*2; j++){large_2_pixel[index][i][j] = 0x00;//默认填充黑色}}}//将图片放大两倍后的像素表for (int i = 0; i<width; i++){for (int j = 0; j<height; j++){large_2_pixel[RGB_R][i * 2][j * 2] = origin_pixel[RGB_R][i][j];large_2_pixel[RGB_G][i * 2][j * 2] = origin_pixel[RGB_G][i][j];large_2_pixel[RGB_B][i * 2][j * 2] = origin_pixel[RGB_B][i][j];}}//显示被放大两倍后未进行插值处理的图片for (int i = 0; i<width * 2; i++){for (int j = 0; j<height * 2; j++){int r_pixel, g_pixel, b_pixel;r_pixel = large_2_pixel[RGB_R][i][j];g_pixel = large_2_pixel[RGB_G][i][j];b_pixel = large_2_pixel[RGB_B][i][j];clr = RGB(r_pixel, g_pixel, b_pixel);//逐个像素点绘制pDC->SetPixel(i+width+picture_interval, j+10, clr);}}//对放大两倍的图片进行线性&双线性插值处理,方格3x3int ***bilinear_interpolation_pixel = large_2_pixel;for (int i = 0; i<width * 2 - 2; i += 2){for (int j = 0; j<height * 2 - 2; j += 2){bilinear_interpolation_pixel[RGB_R][i][j + 1] = (bilinear_interpolation_pixel[RGB_R][i][j] + bilinear_interpolation_pixel[RGB_R][i][j + 2]) / 2;bilinear_interpolation_pixel[RGB_R][i + 2][j + 1] = (bilinear_interpolation_pixel[RGB_R][i + 2][j] + bilinear_interpolation_pixel[RGB_R][i + 2][j + 2]) / 2;bilinear_interpolation_pixel[RGB_R][i + 1][j] = (bilinear_interpolation_pixel[RGB_R][i][j] + bilinear_interpolation_pixel[RGB_R][i + 2][j]) / 2;bilinear_interpolation_pixel[RGB_R][i + 1][j + 2] = (bilinear_interpolation_pixel[RGB_R][i][j + 2] + bilinear_interpolation_pixel[RGB_R][i + 2][j + 2]) / 2;bilinear_interpolation_pixel[RGB_R][i + 1][j + 1] = (bilinear_interpolation_pixel[RGB_R][i + 1][j] + bilinear_interpolation_pixel[RGB_R][i + 1][j + 2]) / 2;bilinear_interpolation_pixel[RGB_G][i][j + 1] = (bilinear_interpolation_pixel[RGB_G][i][j] + bilinear_interpolation_pixel[RGB_G][i][j + 2]) / 2;bilinear_interpolation_pixel[RGB_G][i + 2][j + 1] = (bilinear_interpolation_pixel[RGB_G][i + 2][j] + bilinear_interpolation_pixel[RGB_G][i + 2][j + 2]) / 2;bilinear_interpolation_pixel[RGB_G][i + 1][j] = (bilinear_interpolation_pixel[RGB_G][i][j] + bilinear_interpolation_pixel[RGB_G][i + 2][j]) / 2;bilinear_interpolation_pixel[RGB_G][i + 1][j + 2] = (bilinear_interpolation_pixel[RGB_G][i][j + 2] + bilinear_interpolation_pixel[RGB_G][i + 2][j + 2]) / 2;bilinear_interpolation_pixel[RGB_G][i + 1][j + 1] = (bilinear_interpolation_pixel[RGB_G][i + 1][j] + bilinear_interpolation_pixel[RGB_G][i + 1][j + 2]) / 2;bilinear_interpolation_pixel[RGB_B][i][j + 1] = (bilinear_interpolation_pixel[RGB_B][i][j] + bilinear_interpolation_pixel[RGB_B][i][j + 2]) / 2;bilinear_interpolation_pixel[RGB_B][i + 2][j + 1] = (bilinear_interpolation_pixel[RGB_B][i + 2][j] + bilinear_interpolation_pixel[RGB_B][i + 2][j + 2]) / 2;bilinear_interpolation_pixel[RGB_B][i + 1][j] = (bilinear_interpolation_pixel[RGB_B][i][j] + bilinear_interpolation_pixel[RGB_B][i + 2][j]) / 2;bilinear_interpolation_pixel[RGB_B][i + 1][j + 2] = (bilinear_interpolation_pixel[RGB_B][i][j + 2] + bilinear_interpolation_pixel[RGB_B][i + 2][j + 2]) / 2;bilinear_interpolation_pixel[RGB_B][i + 1][j + 1] = (bilinear_interpolation_pixel[RGB_B][i + 1][j] + bilinear_interpolation_pixel[RGB_B][i + 1][j + 2]) / 2;}}//显示经过线性&双线性插值处理后的图片for (int i = 0; i<width * 2; i++){for (int j = 0; j<height * 2; j++){int r_pixel, g_pixel, b_pixel;r_pixel = large_2_pixel[RGB_R][i][j];g_pixel = large_2_pixel[RGB_G][i][j];b_pixel = large_2_pixel[RGB_B][i][j];clr = RGB(r_pixel, g_pixel, b_pixel);//逐个像素点绘制pDC->SetPixel(i + width + picture_interval + width*2 + picture_interval, j + 10, clr); }}//释放占用的资源for( int i=0; i<3; i++ ){for( int j=0; j<width * 2; j++ ){delete bilinear_interpolation_pixel[i][j];}delete bilinear_interpolation_pixel[i];}delete bilinear_interpolation_pixel;ReleaseDC(pDC);         origin_image.Detach();
...(省略无关部分)

效果展示

如下图所示,左边是原图,中间的是原图放大2倍后未进行插值的图片,右边是原图放大2倍后进行双线性插值的图片:
这里写图片描述
很明显看出,未经过任何处理的放大后的图(中间)与原图(最左边)匹配度低,经过双线性插值的图片(最右边)与原图(最左边)匹配度很高.
最后想说的是CSDN里的markdown使用MathJax渲染真是不顺手,整理数学公式比整理思路时间还多!