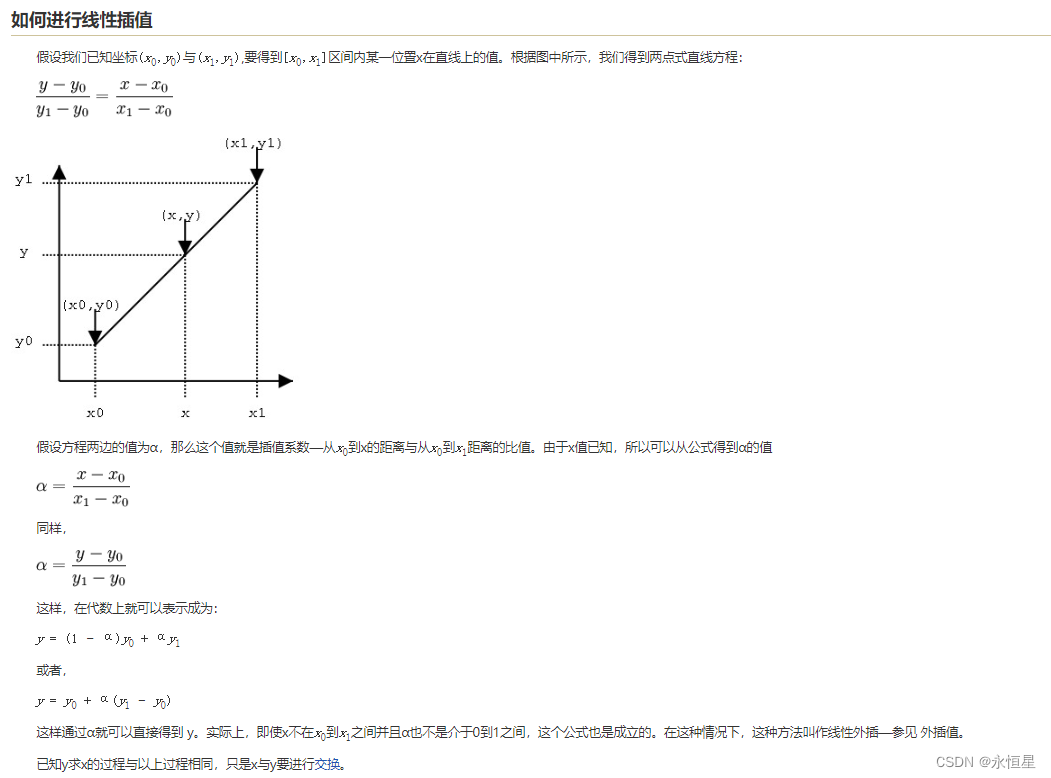
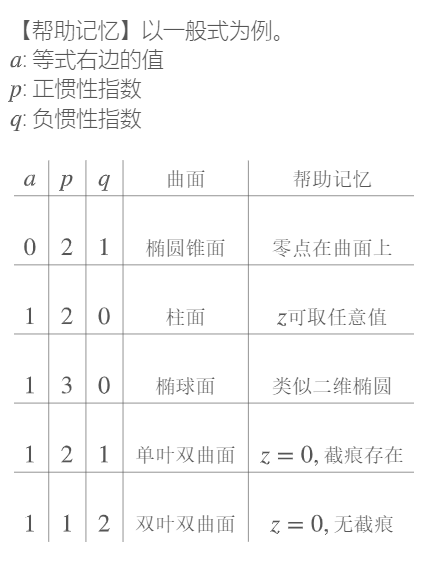
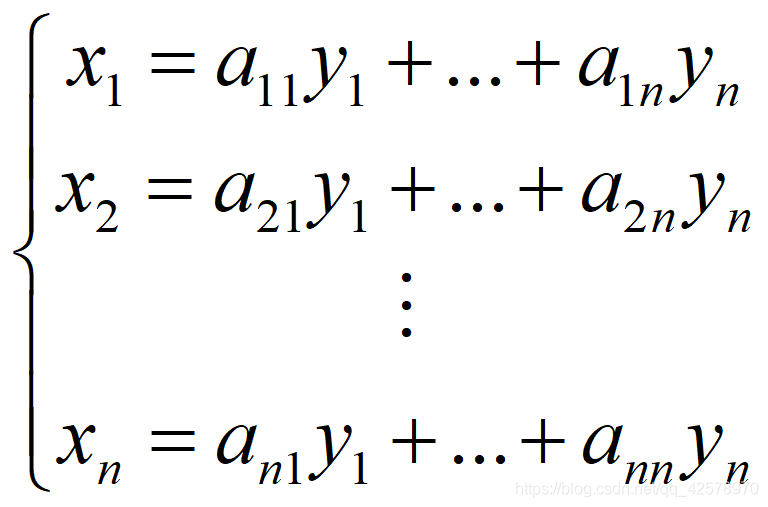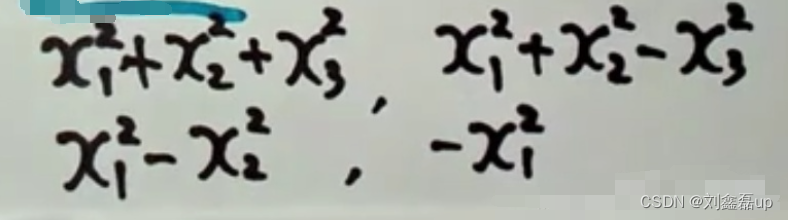最近在学数字图像处理中旋转变换的问题，发现旋转以后图片有一些不连续点，于是试着用双线性插值法进行解决。下面就介绍下插值的原理：

线性插值

如果你只处理分离的数据、想知道分离点之间的某些值，需要用到某种类型的插值。这种情况如图5-17坐标所示。对某些分离的(整数) X值，你知道Y值。当X=2，你知道Y=10，X=3时Y=30。但你不知道X=2.7时的Y值。

使用线性插值，你通过连接两点的线段找到X=2.7对应的Y值，如图1所示。使用线性插值，通过连接两点的线段找到X=2.7对应的Y值。线性插值总是将X表达成0和1之间，0对应X的最小值（你知道对应的Y值，本例中为2），1对应X的最大值（本例中为3） 。本例中你想找到X=2.7时的Y值，结果是0.7，意思是“2和3至之间的70%。”

在图1的左图中，0%对应Y值10，100%对应Y值20，所以70%对应Y=17。这很容易看出，但右图的情况如何？14对应0.33，因为它是13和16之间的33%。但35和46之间的33%是多少？显然，你希望有代码可以为你计算结果。

首先要有代码找到0和1对应的值。从X值开始，首先减去最小的X值，这样最小值变为0。然后，将最大值缩放为1，你可以通过将它除以最大值和最小值之差实现。

下面是图1左图的做法： 2.7→(2.7－min)/(max－min)=(2.7－2)/(3－2)=0.7

然后，进行逆运算获取对应的Y值：首先缩放这个值(通过乘以最大值和最小值的差值)，并加到最小的Y值上：

0.7* (maxY－min Y)＋minY=0.7*(20－10)＋10=0.7*10＋10=17

这里你采取图1左图简单例子的规则，但你可以使用这个方法计算任何线性插值。看一下图1右图更难的例子，在这种情况中，你知道X=13对应Y=35，X=16对应Y=46，但你想知道X=14对应的Y值。所以，首先获取0和1之间对应的值：

14→(14－minX)/(maxX－minX) =(14－13)/(16－13)=0.33

知道了对应值，就做好了获取对应Y值的准备：

0.33* (maxY－minY)＋minY=0.33*(46－35)＋35=0.33*11＋35=3.67＋35=38.67

最后，需要进行浮点计算。图5-17的右图中找到X=1