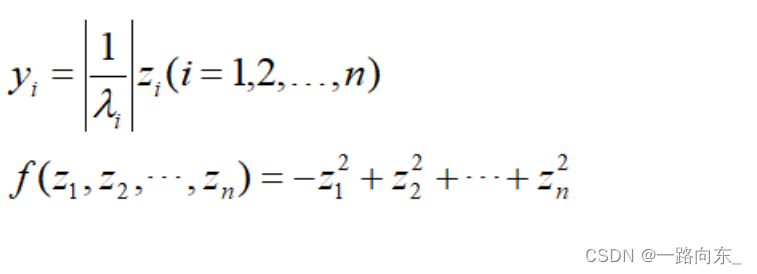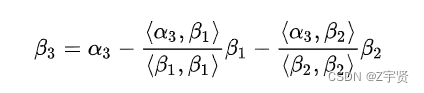常用线性插值的介绍和应用

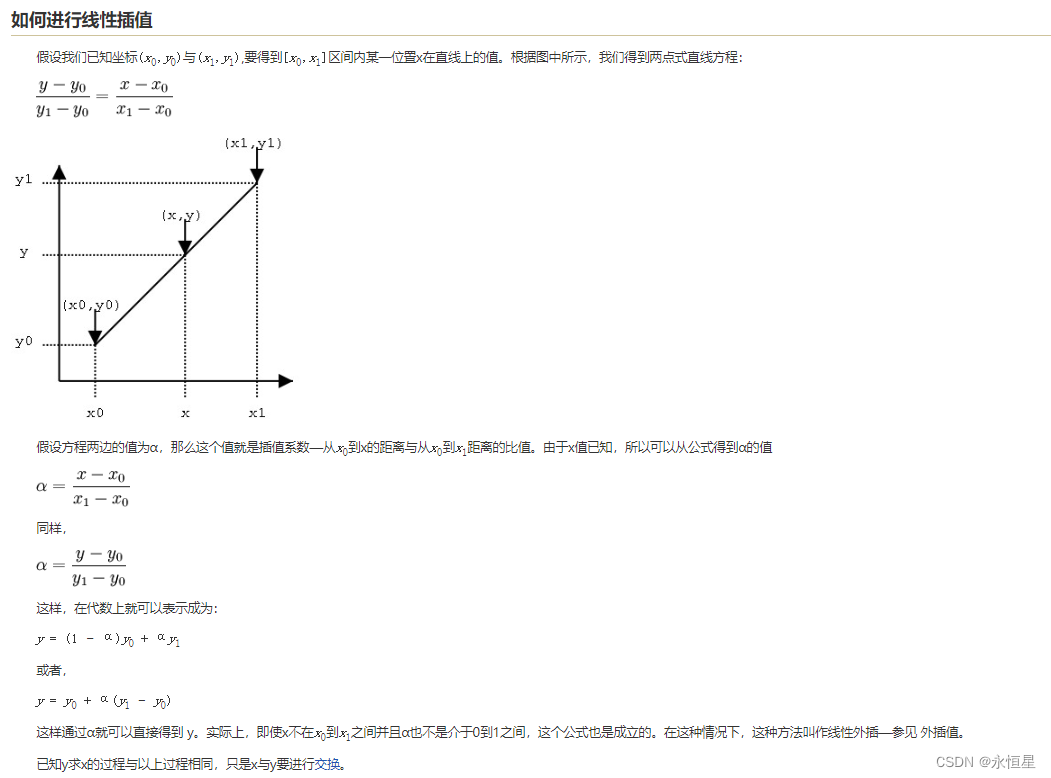
线性插值

插值是计算机图形学中非常常用的技术。通常，数据是在常规网格上指定的（值写在2D或3D网格的顶点位置）或在线上（在一维的情况下），但是程序需要在该网格上的随机位置求值。如果样本位于网格顶点上，那么我们可以简单地使用存储在网格顶点上的值。但是，如果样本位于网格上其他任何位置（单元中的某个位置），则考虑到那里没有数据，我们需要通过平均存储在单元顶点处的值来计算一个。这项技术称为插值，因为关键思想是在固定的网格位置“插值”现有值以计算网格上其他任何位置的值。

在2D中，该技术称为双线性插值。它的3D对应物称为三线性插值。线性插值的方程式：

目标点(下图符号？处)的属性值由上述公式给出。其中a和b分别为两个端点处的属性值，t的值为目标点到a的距离与a到b的距离比值(t在0到1的范围内)，我们示例图如下：

与重心坐标类似，未知点的属性都是由端点属性和对立权重的加权和。即始终是左方端点a乘对立权重(1-t)，加上右方端点b乘对立权重t。下面的双线性插值和三线性插值更为直观。

双线性插值

当我们需要知道规则2D网格上随机位置的值时，可以使用双线性插值。注意，该网格也可以是图像或纹理贴图。如下示例：

我们希望在绿点(具有坐标cx，cy的c)标记的位置插值出一个值。为了计算c的值，我们将首先在一个方向(x方向)上执行两次线性插值，获得a和b。我们将使用tx对c00-c10和c01-c11进行线性插值以获得a和b。然后，我们将沿第二方向(y轴)线性插值a-b，以使用ty获得c。无论是开始沿x轴还是沿y轴对前两个值进行插值，都没有任何区别。在我们的示例中，我们首先对c00-c10和c01-c11进行插值以获得a和b。我们也可以先使用ty从c00-c01和c10-c11插值，然后使用tx插值结果。值得注意的是，双线性插值不再是线性的了，因为它是两个线性函数的乘积。如果采样点位于单元格的边缘之一(线c00-c10或c00-c01或c01-c11或c10-c11)上，则该函数为线性。在其他任何地方都是二次方。双线性插值代码如下：

float bilinear( const float &tx, const float  &ty, const Vec3f &c00, const Vec3f &c10, const Vec3f &c01, const Vec3f &c11) 
{ 
#if 1 //两步计算float  a = c00 * (1 - tx) + c10 * tx; float  b = c01 * (1 - tx) + c11 * tx; return a * (1) - ty) + b * ty; 
#else //面积计算return (1 - tx) * (1 - ty) * c00 + tx * (1 - ty) * c10 + (1 - tx) * ty * c01 + tx * ty * c11; 
#endif 
}

我们上面讲解的是分成两步计算，我们还可以用上面提到的重心坐标的理解方法，使用面积计算。未知点属性由：端点属性乘对立面积乘积，再对四个端点都进行此操作并求和。c00端点操作如下：

如上图，c00点的属性乘上右上角矩形的面积。同理c10点的属性要乘上左上角的矩形，c01乘上右下角的矩形，c11乘上左下角的矩形。我们根据面积的代码就根据此得出。

三线性插值

三线性插值又是双线性插值的拓展。我们若想计算随机三维空间的点，如下图：

使用分步法来实现：为了计算e和f，我们使用两个双线性插值。为了计算g，我们沿z轴线性插值e和f。实现代码如下：

Vec3<T> interpolate(const Vec3<T>& location) { T gx, gy, gz, tx, ty, tz; unsigned gxi, gyi, gzi; // 获取网格点坐标(我们定义的网格为单位网格。长，宽，高为1)gx = location.x * nvoxels; gxi = int(gx); tx = gx - gxi; gy = location.y * nvoxels; gyi = int(gy); ty = gy - gyi; gz = location.z * nvoxels; gzi = int(gz); tz = gz - gzi; const Vec3<T> & c000 = data[IX(gei, gyi, gzi)]; const Vec3<T> & c100 = data[IX(gxi + 1, gyi, gzi)]; const Vec3<T> & c010 = data[IX(gxi, gyi + 1, gzi)]; const Vec3<T> & c110 = data[IX(gxi + 1, gyi + 1, gzi)]; const Vec3<T> & c001 = data[IX(gxi, gyi, gzi + 1)]; const Vec3<T> & c101 = data[IX(gxi + 1, gyi, gzi + 1)]; const Vec3<T> & c011 = data[IX(gxi, gyi + 1, gzi + 1)]; const Vec3<T> & c111 = data[IX(gxi + 1, gyi + 1, gzi + 1)]; 
#if 1 //分步处理，先进行2次双线性插值，再在z方向做线性插值Vec3<T> e = bilinear<Vec3<T> >(tx, ty, c000, c100, c010, c110); Vec3<T> f = bilinear<Vec3<T> >(tx, ty, c001, c101, c011, c111); return e * ( 1 - tz) + f * tz; 
#else //利用体积计算return (T(1) - tx) * (T(1) - ty) * (T(1) - tz) * c000 + tx * (T(1) - ty) * (T(1) - tz) * c100 + (T(1) - tx) * ty * (T(1) - tz) * c010 + tx * ty * (T(1) - tz) * c110 + (T(1) - tx) * (T(1) - ty) * tz * c001 + tx * (T(1) - ty) * tz * c101 + (T(1) - tx) * ty * tz * c011 + tx * ty * tz * c111; 
#endif }

同样，我们还给出了利用体积求解三线性插值的方法。该方法依旧是重心坐标处理的拓展。c00和对立体积想乘，示例图如下：

同理另外7个点也根据此过程计算端点和对立体积的乘积，最后对8个端点求和便能得出最终插值属性。

三线性插值典型应用的例子是在mipmap中，我们用(u，v，d)三元组访问mipmap。值d为访问的mipmap的层级，可以为小数。采样高于d位置的纹理级别(整数)和低于d位置的级别(整数)(若d=3.5，则访问层级3和4的贴图)。(u，v)位置用于从这两个纹理级别的每一个中检索双线性插值样本。然后根据从每个纹理级别到d的距离对生成的样本进行线性插值。整个过程称就为三线性插值，且每个像素执行一次。

双线性插值和平滑曲线插值对比

在我们处理纹理贴图时，可选参数为NEAREST(最近)，和LINEAR(双线性)。Qu ́ılez在文章“improved texture interpolation” 中提出了一种简单的技术，使用平滑曲线在一组2×2纹素之间进行插值。平滑曲线常用的为平滑步幅曲线和五次曲线：

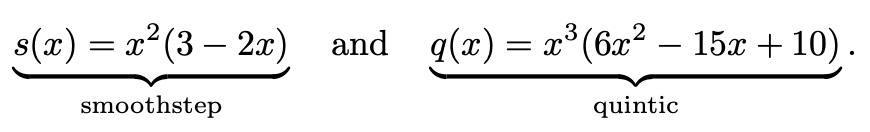
左侧为平滑步幅曲线，右侧为五次曲线。平滑步幅曲线在0和1处有一阶导数为0的特点，即s'(0)=0，s'(1)=0。而5次曲线不仅0和1处的一阶导数为0，其二阶导数也为0，即s''(0)=0，s''(1)=0。两条曲线如下图所示：

我们观察放大一维纹理这些方法的对比图。橙色圆圈表示纹理像素的中心以及纹理像素值(高度)。从左到右：最近的，线性的，5次曲线插值，三次插值。

后面两种能给出平滑的改观。

Qu ́ılez方法过程如下：

将纹理坐标乘上纹理尺寸，然后加上0.5，用p保存结果。
将p取整，并保存在i中。
用p减去i获取小数部分，并保存在f中。
用平滑曲线函数处理f，即f=func(f)；
将f和整数部分i相加，保存在p中。
将p减去0.5，再去除以纹理尺寸。

我们过程代码如下：

vec2 smoothst(vec2 tex){float u=tex.x*tex.x*(3.0-2.0*tex.x);float v=tex.y*tex.y*(3.0-2.0*tex.y);return vec2(u,v);
}vec2 quintic(vec2 tex){float u=tex.x*tex.x*tex.x*(6.0*tex.x*tex.x-15.0*tex.x+10);float v=tex.y*tex.y*tex.y*(6.0*tex.y*tex.y-15.0*tex.y+10);return vec2(u,v);
}vec4 getTexel( vec2 p )
{p = p*myTexResolution + 0.5;vec2 i = floor(p);vec2 f = p - i;f = quintic(f);p = i + f;p = (p - 0.5)/myTexResolution;return texture2D( myTex, p );
}

双线性插值效果和利用五次曲线平滑效果对比如下：