各位博友们大家好,小弟遇到一些问题经常会去看大家的博客,所以也想加入大伙的阵营,每每看到一些好的东西,有些心得体会什么的也想与大伙分享。
1.关于插值
插值,它根据已知的数据序列(也可以理解为坐标中一连串离散的点),找到其中的规律;然后根据找到的这个规律,来对其中尚未有数据记录的点进行数值估计。
基于这样一种功能,我目前知道的应用是:1)它可以对数据中的缺失进行合理的补偿;2)它可以对数据进行放大或者缩小。当然还有别的功能,这个大家自己遇到的说不定比我多很多。
2.1.关于线性插值
线性插值是一种针对一维数据的插值方法,它根据一维数据序列中需要插值的点的左右邻近两个数据点来进行数值的估计。当然了它不是求这两个点数据大小的平均值(当然也有求平均值的情况),而是根据到这两个点的距离来分配它们的比重的。
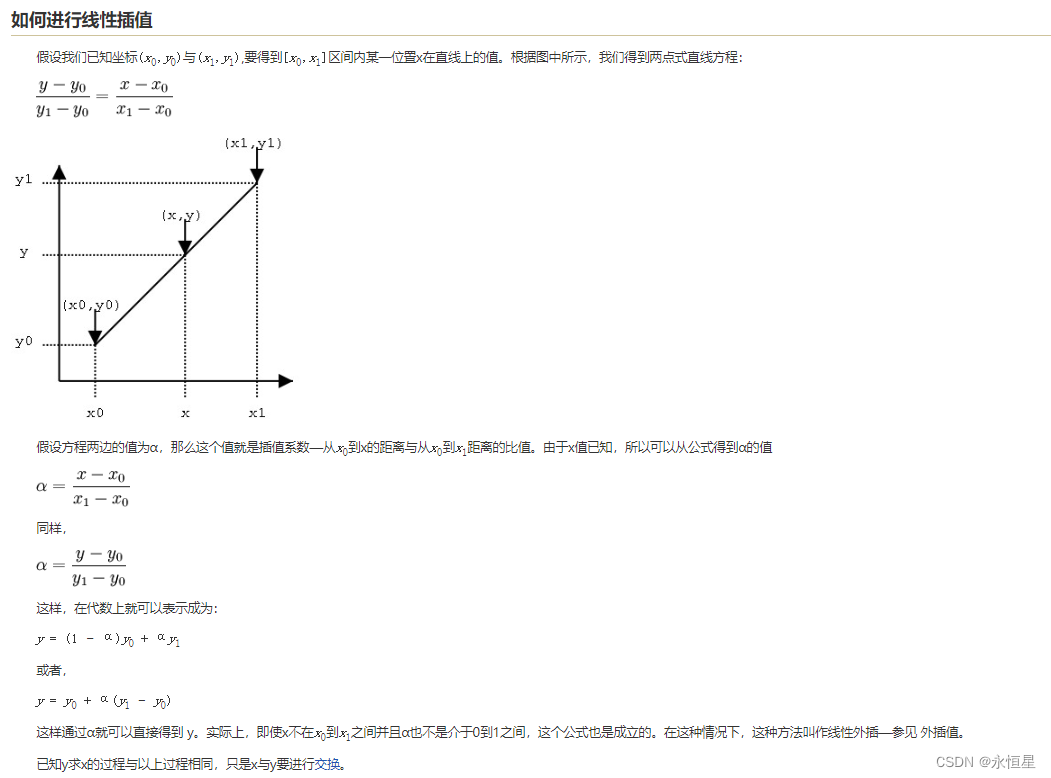
这里我用了一张来自https://zh.wikipedia.org/wiki/%E7%BA%BF%E6%80%A7%E6%8F%92%E5%80%BC的图,它很好地显示了线性插值的原理。根据图中的假设:已知点(x0,y0)、(x1,y1),试问在x处插值,y的值是多少?用我们初中学过的知识,已知两个点的坐标可以得到一条线,又已知线上一点的一个坐标可以求得这个点的另一个坐标值。这就是线性插值的原理。
这样就求得了y值。
2.2.线性插值举例
假如一天中,我测得了其中7个时间点的温度。1点、3点、8点、12点、15点、20点、24点摄氏度分别是8、9、16、23、22、18、10。请问用线性插值的方法得到这一天中1点到24点之间其他时间点的温度该怎么做?(线性插值是属于内插法,要去求这一天1点到24点以外的数据就不行了)
数据小,计算量小,用手算就行,但是数据大,我们就只要借助计算机了,所以我还是用计算机求吧:
法1:matlab有插值函数,interp1(),直接用就可以:
---------------------------------------------------
time = [1 3 8 12 15 20 24];
tem = [8 9 16 23 22 18 10];
time_i = 1:0.01:24;
tem_i = interp1(time,tem,time_i,'linear');
plot(time,tem,'o',time_i,tem_i);
---------------------------------------------------
其中,如果你想知道其中某几个点的温度值,修改变量time_i就可以了,插值得到的对应time_i的温度值都存放在tem_i变量中。
法2:自己写一个interp1类似的东东,也可以完成任务:(小弟给大家献丑了)
建立一个m-file:取名self_interp1.m,内容如下:
----------------------------------------------------
% 自己写一个interp1类似功能的接口
% 这个接口中参数x需要是从小到大的序列,y则是随意
function [yi] = self_interp1(x,y,xi,method)
% 初始化yi,给它xi对应的列
col_xi = size(xi,2);
yi = zeros(1,col_xi);
% 检测使用的插值方法 这里期望的是'linear'
if strcmp(method,'linear'),
% 找到每个xi在x序列中的位置
col_x = size(x,2);
for i = 1:col_xi,
for j = 1:col_x-1,
% 假如需要计算插值公式
if x(j+1) > xi(i),
yi(i) = y(j)+(y(j+1)-y(j))/(x(j+1)-x(j))*(xi(i)-x(j));
break;
end
% 假如插值处的数据已经测得了,就直接把值给它,节约计算资源
if x(j) == xi(i),
yi(i) = y(j);
break;
end
end
% 以上没有把最后一个数据点考虑进去,需要加上
yi(col_xi) = y(col_x);
end
else
error('插值方法请选择(linear)\n');
end
end
----------------------------------------------------
接着像法1一样,只是原先的interp1()函数,在这里改成我们自己的self_interp1(),如下:
----------------------------------------------------
time = [1 3 8 12 15 20 24];
tem = [8 9 16 23 22 18 10];
time_i = 1:0.01:24;
tem_i = self_interp1(time,tem,time_i,'linear');
plot(time,tem,'o',time_i,tem_i);
----------------------------------------------------
结果如下:
结果看起来一样一样的,幸好没有让各位大哥失望。
第一次写博客,写的很慢,下次再来和各位老哥一起学习双线性插值。
PS: 本文允许所有人转载。