前言:
{
最近特别忙(或者说时间规划出了问题),所以更新的都是短篇。
本次的内容是最大类间方差法(大津法,Otsu)。
}
正文:
{
根据[1]中的介绍,大津法的主要作用是二值划分(求阈值)。其原理非常简单,就是求式(1)最大时其中t的值。
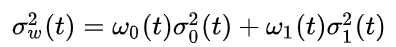
其中两个ω分别代表类0和类1的数据所占比例(权值),两个σ2分别代表类0和类1的数据的方差,所以最小化的式(1)就是最小类内方差。
另外,式(2)证明了式(1)的最小类内方差就是最大类间方差。
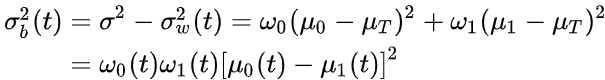
其中u0,u1和uT分别为类0的数据的期望,类1的数据的期望和所有数据的期望。
由此可见最大类间方差法这个名字的由来。
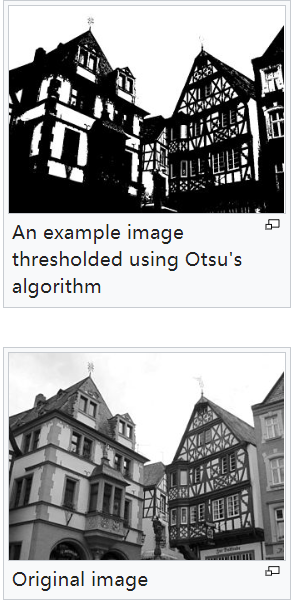
图1是在某个案例下阈值与类间方差的关系。图2是本方法在一张灰度图上的应用。

}
结语:
{
这个方法我见到过很多次,但没有仔细了解过,现在发现其实这算法还不算复杂。
说实话,式(2)的推导我还没完全搞明白,不过目前实践更重要,我想把时间留给代码调试。
参考资料:
{
[1]https://en.wikipedia.org/wiki/Otsu%27s_method
}
}