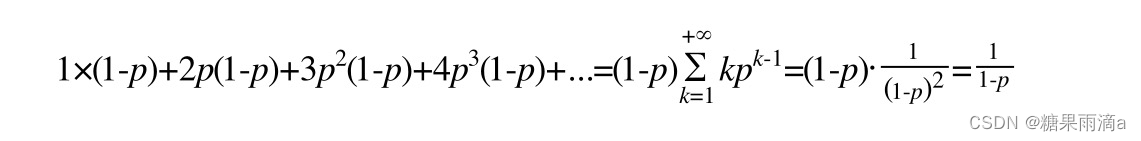目录
一.跳表介绍
二.实现思路
（一）.结点结构
（二）.检索
（三）.插入
（四）.删除
三.实现代码
一.跳表介绍
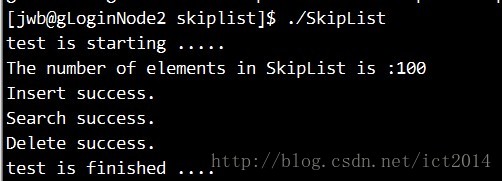
跳表是一种随机化数据结构，主要用于快速检索数据。实质上是一种可以进行二分查找的有序链表。时间复杂度可以达到O(log^n)。在性能上与红黑树、AVL树相当。当然因为结构具有随机性，最坏情况下时间复杂度为O(n)。
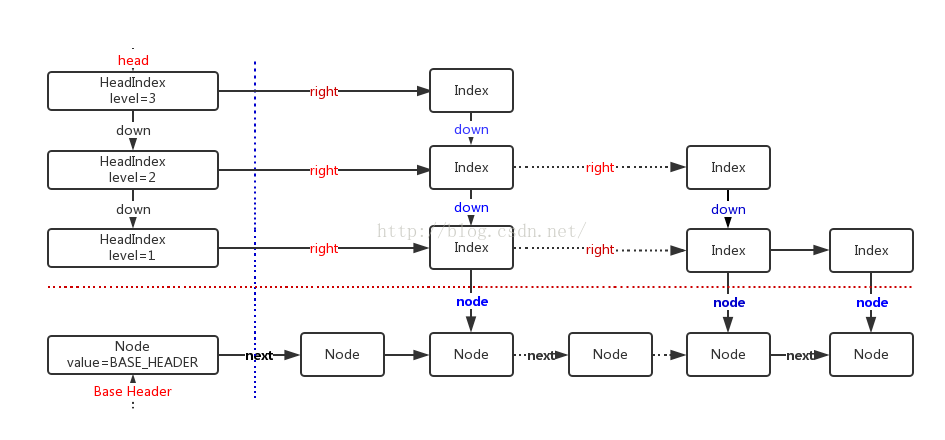
跳表结构如下图：
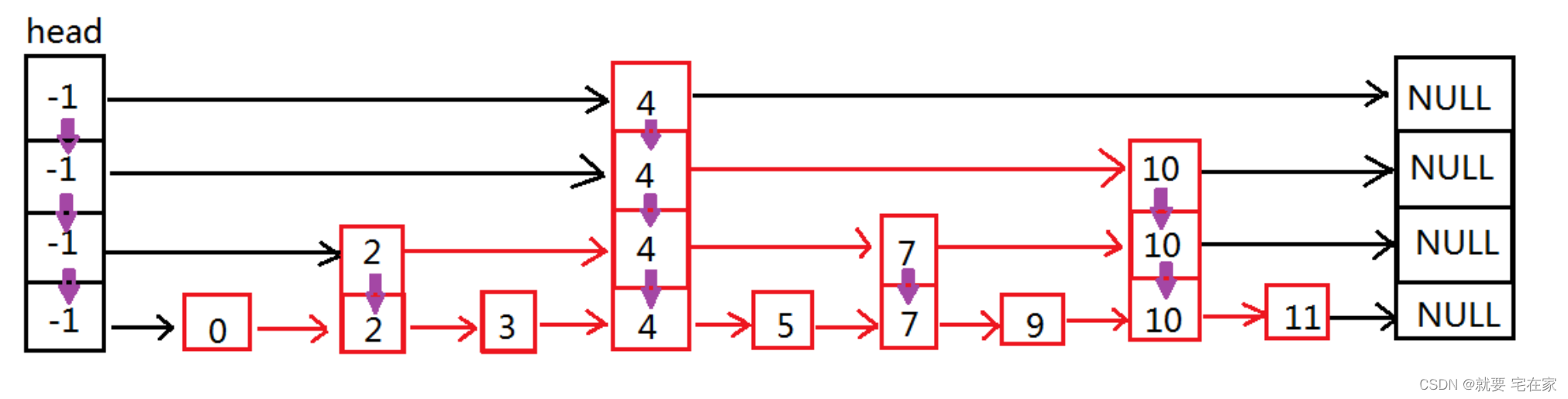与普通链表相比，跳表每个结点有不止一个指向后续的指针，具体数量是随机出来的。这些指针结构上从低到高排列，指向后面与自己同层的指针所在的结点。
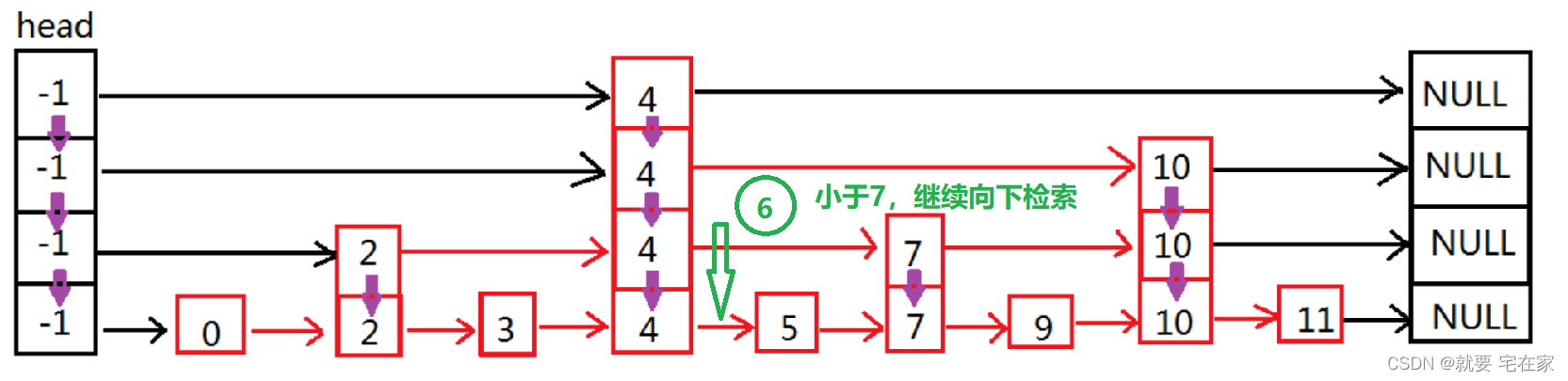
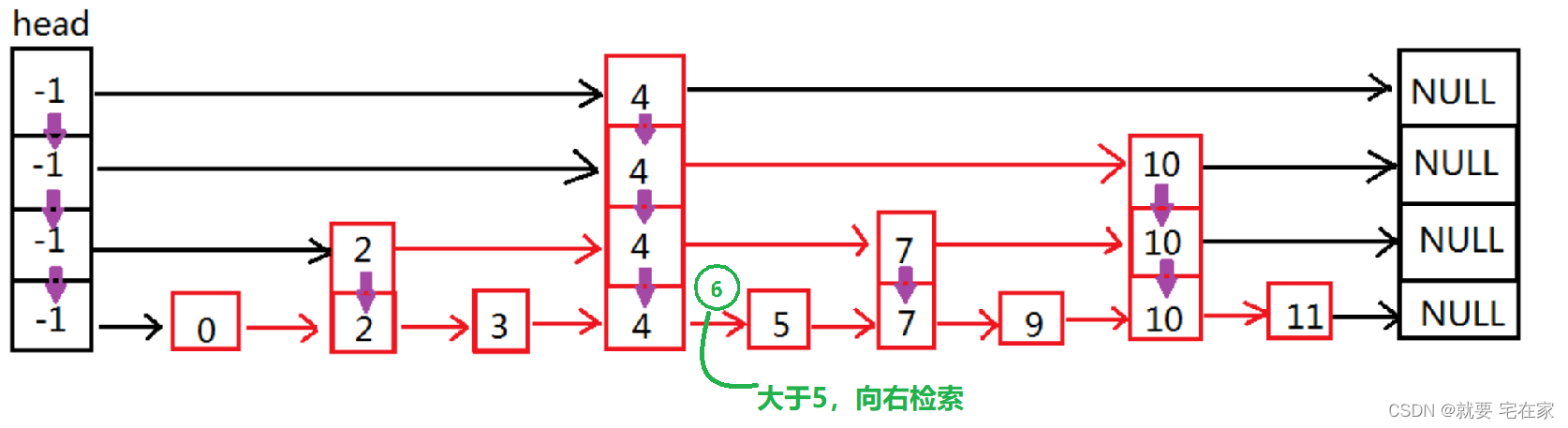
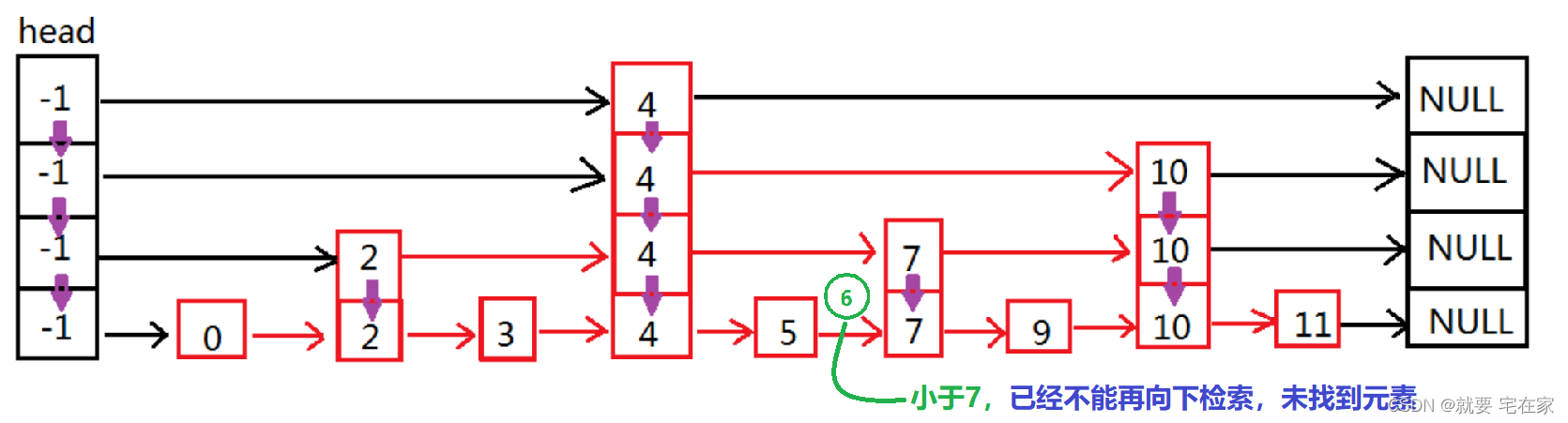
检索数据时，从head结点开始，按指针从高到低的所指元素大小进行比较，直到找到或走到结尾。因为层数越高代表跳过的元素数量越多，因此理论上可以类比二分查找。
查找时可能找到也可能找不到元素：
如果找到元素，以上图为例，假如要检索的是9，那么顺序如下：
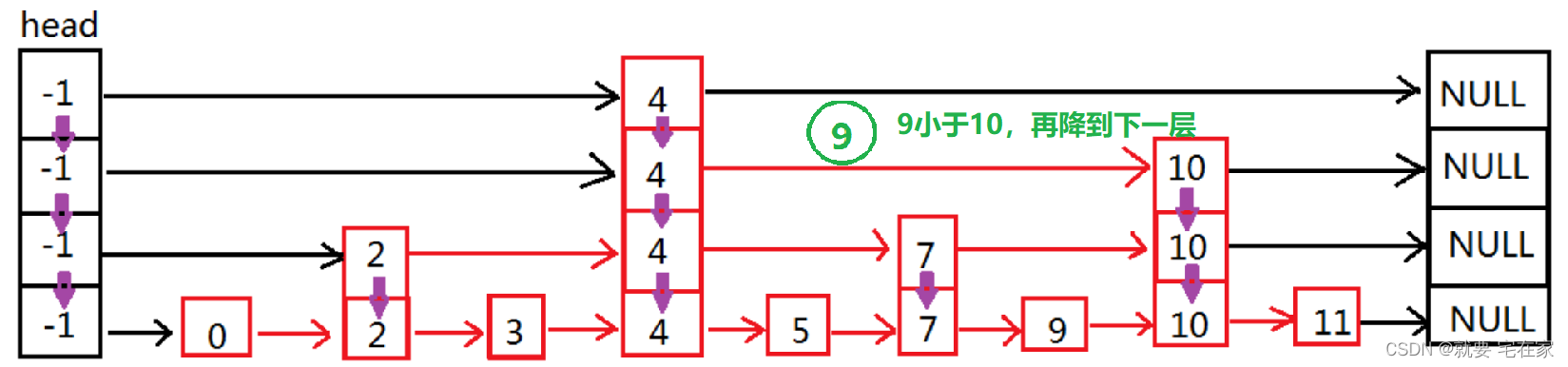
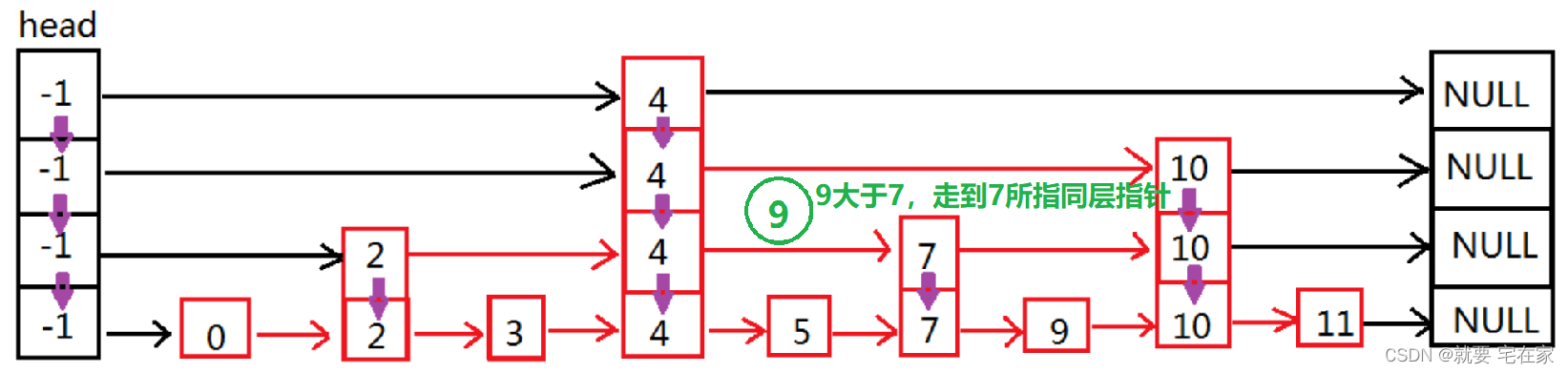
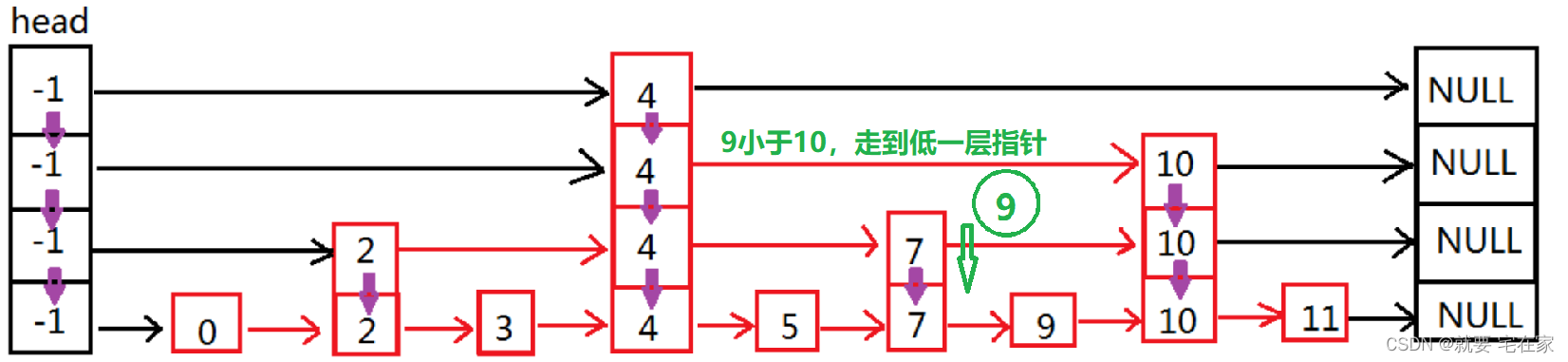
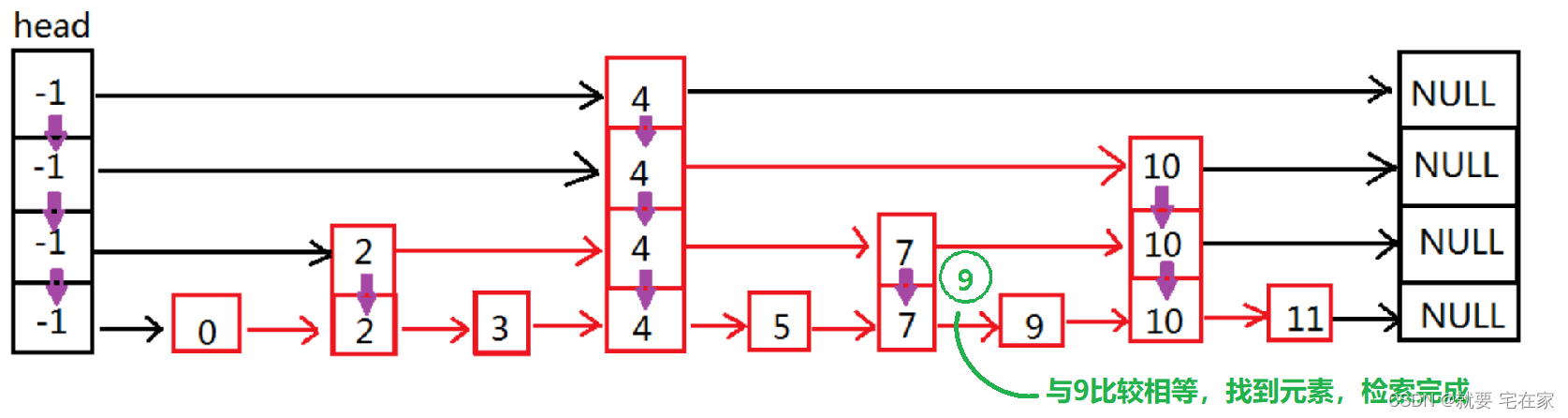
如果是未找到元素，以6为例：
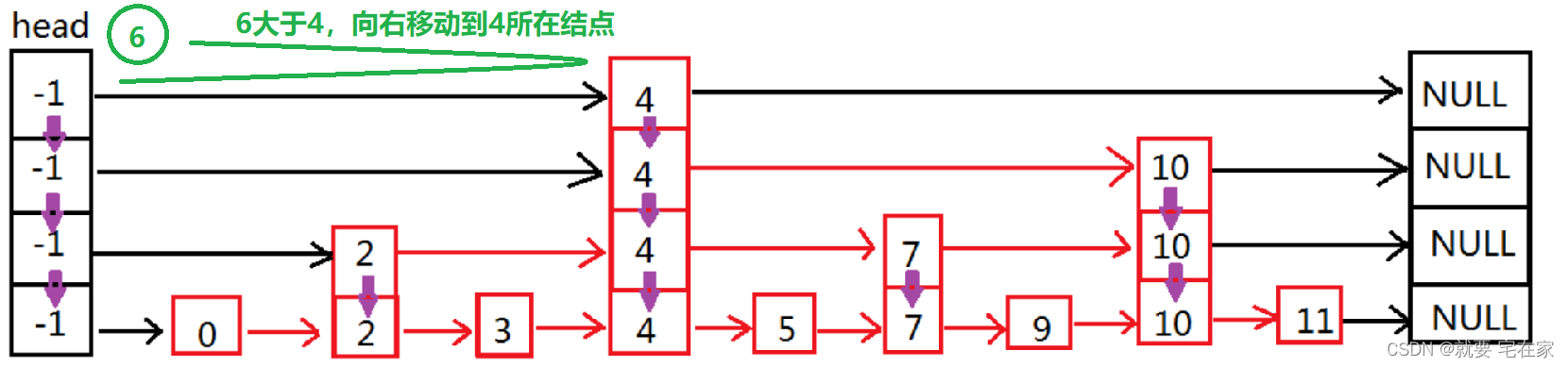
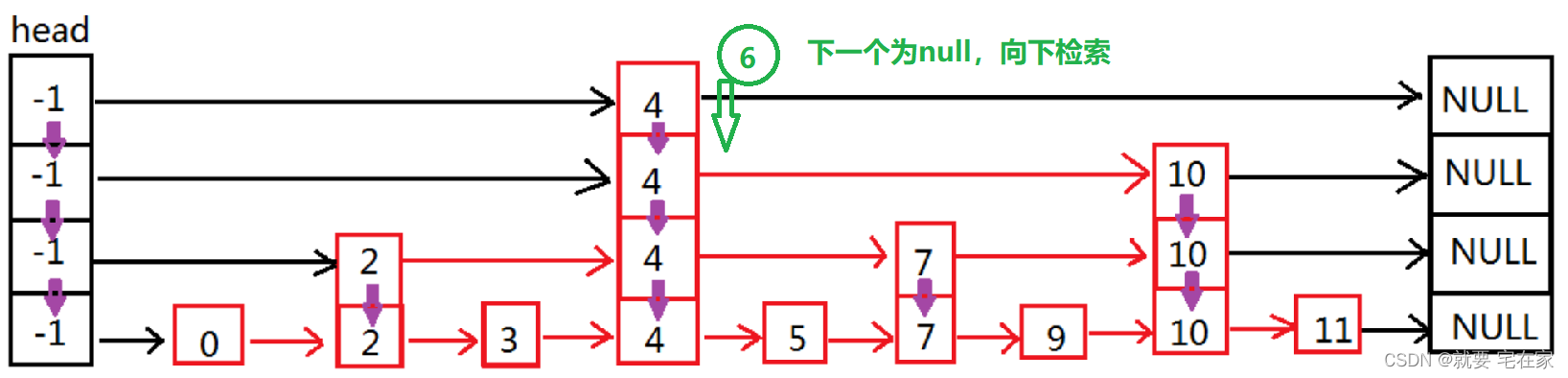
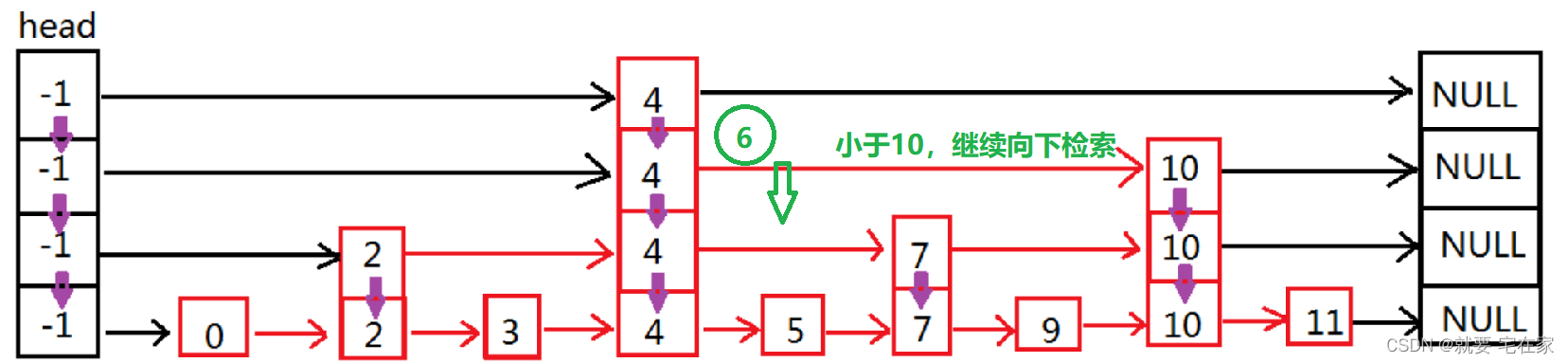
二.实现思路
（一）.结点结构
结点通过结构体封装即可，内部是保存的结点元素值和可变数组，数组每一个元素是指向结点的指针。代码如下：
struct SkiplistNode {//结点int _val;//元素值，没有使用模板，可以自定义模板vector<SkiplistNode*> _skipPoints;//结点指针数组SkiplistNode(int val, int n = 1)//n：指针层数，默认1层:_val(val), _skipPoints(n, nullptr){}~SkiplistNode(){for (auto* p : _skipPoints) p = nullptr;}
};（二）.检索
按照上述检索思路，检索失败的标准是走到结点指针的-1层。每一次检索时判断此时同层的指针所指后续元素大小，大于就走到该后续元素，小于就走到低一层的指针。
代码结构如下：
bool search(int target) {Node* cur = _head;//记录当前结点位置int sub = cur->_skipPoints.size() - 1;//从最高层开始，head层数即最高层数while (sub >= 0) {if (没有走到null && 大于后续结点值){cur = cur->_skipPoints[sub];}else if (走到null || 小于后续结点值){sub--;}else 找到结点}没找到结点
}（三）.插入
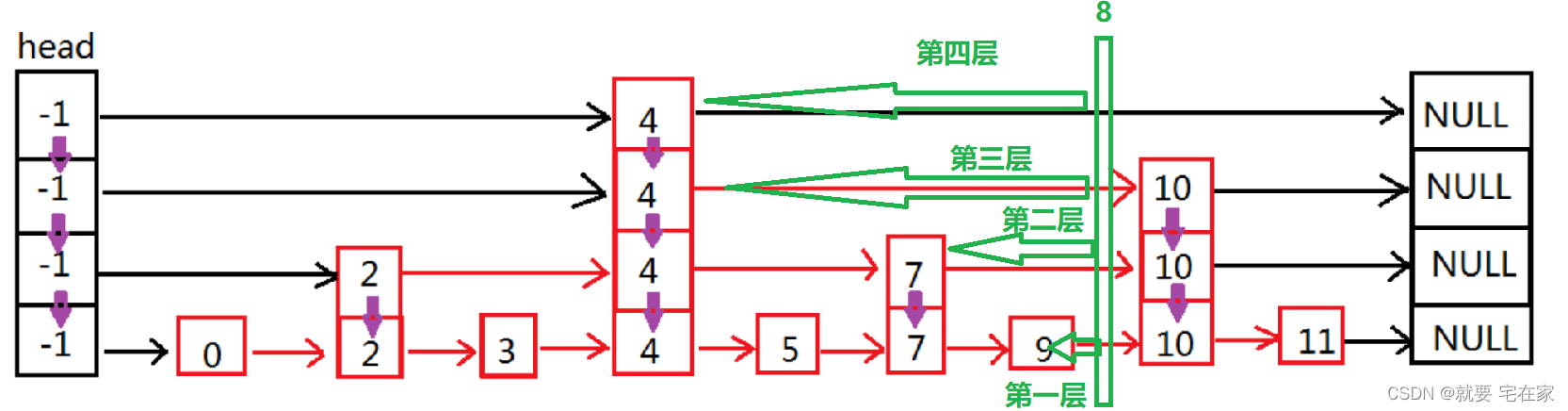
插入元素前，需要确定在哪个结点后插入，但基于跳表结点多层指针结构，每一层指针的前序指针可能不同，因此需要先检索一遍，确定每一层的前序元素结点。
以8为例，插入后，每一层的前序指针不同。
通过数组记录每一层的前序结点，在插入时按照链表的插入方式插入即可。
插入代码结构如下：
//获取前序结点数组，结构与search相似
vector<Node*> getPrev(int target) {vector<Node*> prev(_head->_skipPoints.size(), nullptr);Node* cur = _head;int sub = _head->_skipPoints.size() - 1;while (层数 >= 0) {if (大于后续结点) {cur = cur->_skipPoints[sub];}else if (小于等于后续结点) {prev[sub] = cur;//记录前序结点sub--;//向下走一层}}return prev;
}void add(int num) {vector<Node*> prevPoints = getPrev(num);//专门记录插入结点的前序指针的数组if (prevPoints[0]记录下一个结点元素与插入值相同) return;//重复添加int i = getLevel();//获取随机层数Node* cur = new Node(num, i);if (随机层数比现有要高) {_head和prevPoints都要增加至i层}for (i -= 1; i >= 0; i--) {按普通链表插入即可}
}同时，因为跳表每个结点有多少层指针是随机的，因此需要写一个随机函数确定层数：
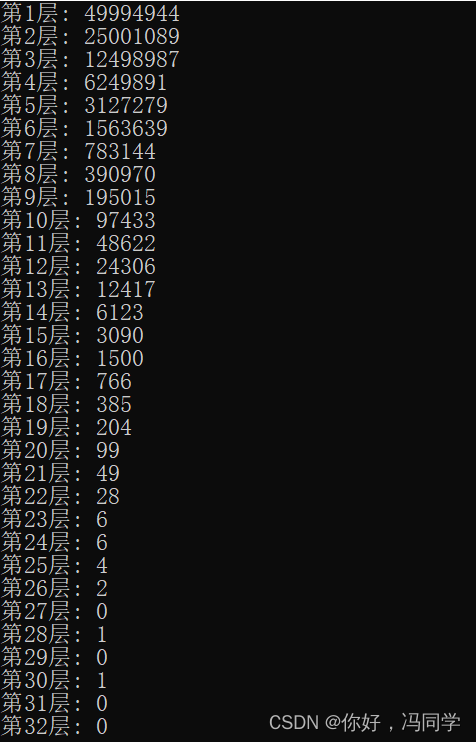
结点每增加一层的概率为p，同时设定最大层数值。
| 层数 | 概率 |
|---|---|
| 一 | 1 - p |
| 二 | p * (1 - p) |
| 三 | p * p * (1 - p) |
根据表格可知，p越小结点增加层数的概率越低。
随机函数可以使用C++随机数库实现：
int getLevel() {//使用随机数库static std::default_random_engine generator(std::chrono::system_clock::now().time_since_epoch().count());//随机数范围0 - 1，类型是doublestatic std::uniform_real_distribution<double> distribution(0.0, 1.0);int level = 1;//如果随机数小于_p同时没达到最大层数，层数++while (distribution(generator) <= _p && level < _maxLevel){++level;}return level;
}（四）.删除
删除元素同样要先找到每一层的前序结点。
之后删除时按照普通链表的方式删除即可。
同时如果删除的结点拥有唯一最高层，那么需要更新_head结点层数。
代码结构如下：
bool erase(int num) {//获取各层前序结点vector<Node*> prevPoints = getPrev(num);//没有该节点if (前序指针指向空 || 前序指向元素不是目标删除元素) {return false;}//获取待删除元素的结点，一层层删除for () {//...}//更新高度return true;
}三.实现代码
元素以int为例，可以使用template变成模板类。
struct SkiplistNode {int _val;vector<SkiplistNode*> _skipPoints;SkiplistNode(int val, int n = 1):_val(val), _skipPoints(n, nullptr){}~SkiplistNode(){for (auto* p : _skipPoints) p = nullptr;}
};class Skiplist {typedef SkiplistNode Node;vector<Node*> getPrev(int target) {vector<Node*> prev(_head->_skipPoints.size(), nullptr);Node* cur = _head;int sub = _head->_skipPoints.size() - 1;while (sub >= 0) {if (cur->_skipPoints[sub] && target > cur->_skipPoints[sub]->_val) {cur = cur->_skipPoints[sub];}else if (!cur->_skipPoints[sub] || target <= cur->_skipPoints[sub]->_val) {prev[sub] = cur;sub--;}}return prev;}int getLevel() {static std::default_random_engine generator(std::chrono::system_clock::now().time_since_epoch().count());static std::uniform_real_distribution<double> distribution(0.0, 1.0);int level = 1;while (distribution(generator) <= _p && level < _maxLevel){++level;}return level;}
public:Skiplist() {srand(time(NULL));_head = new Node(-1);}bool search(int target) {Node* cur = _head;int sub = cur->_skipPoints.size() - 1;while (sub >= 0) {if (cur->_skipPoints[sub] && target > cur->_skipPoints[sub]->_val)//target大于下一个值， 继续向后{cur = cur->_skipPoints[sub];}else if (!cur->_skipPoints[sub] || target < cur->_skipPoints[sub]->_val)//target小于， 向下{sub--;}else return true;}return false;}void add(int num) {vector<Node*> prevPoints = getPrev(num);//专门记录插入结点的前序指针的数组//if (prevPoints[0]->_skipPoints[0] && prevPoints[0]->_skipPoints[0]->_val == num) return;//重复添加int i = getLevel();Node* cur = new Node(num, i);if (i > _head->_skipPoints.size()) {//随机层数比现有要高_head->_skipPoints.resize(i, nullptr);prevPoints.resize(i, _head);//让前序指针数组高出的指向_head,这样能将_head与结点相连}for (i -= 1; i >= 0; i--) {cur->_skipPoints[i] = prevPoints[i]->_skipPoints[i];prevPoints[i]->_skipPoints[i] = cur;}}bool erase(int num) {vector<Node*> prevPoints = getPrev(num);//如果前序为空（num大于所有节点值）或 前序下一个不是num(因为getPrev函数获得的是<=num)if (!prevPoints[0]->_skipPoints[0] || prevPoints[0]->_skipPoints[0]->_val != num) {return false;}//获取待删除元素的结点Node* cur = prevPoints[0]->_skipPoints[0];//一层层删除for (int i = cur->_skipPoints.size() - 1; i >= 0; i--) {prevPoints[i]->_skipPoints[i] = cur->_skipPoints[i];}delete cur;int n = _head->_skipPoints.size() - 1;while (n >= 0) {if (_head->_skipPoints[n] == nullptr) n--;else break;}_head->_skipPoints.resize(n + 1);return true;}
private:Node* _head;size_t _maxLevel = 32;double _p = 0.25;
};信念和目标，必须永远洋溢在程序员内心——未名
如有错误，敬请斧正
