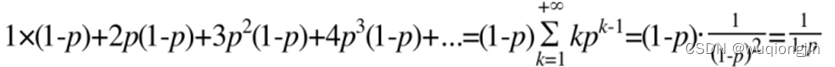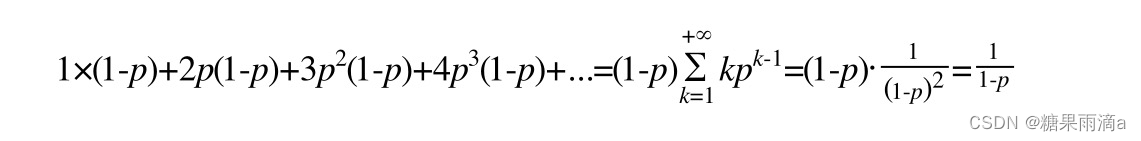Redis 中的底层数据结构：SkipList

article/2025/8/7 21:43:37

一、SkipList 简介

SkipList(5.0) 是zset的底层实现之一，它的数据结构定义如下：

/* ZSETs use a specialized version of Skiplists */
typedef struct zskiplistNode {sds ele; //成员对象double score; //分值struct zskiplistNode *backward; //后退指针//层struct zskiplistLevel {struct zskiplistNode *forward; //前进指针unsigned long span; //跨度} level[];
} zskiplistNode;typedef struct zskiplist {struct zskiplistNode *header, *tail; //头结点，尾节点unsigned long length; //跳表长度int level; //当前最大层高
} zskiplist;typedef struct zset {dict *dict; //跳表中的所有键值对zskiplist *zsl;
} zset;

注意以下几点：

  • header指向头结点，头结点的层高始终为64层
  • level保存跳表中节点层数最高值，但是不计算头结点的层高
  • length保存跳表中节点个数，但是不包括头结点
  • tail指向尾节点

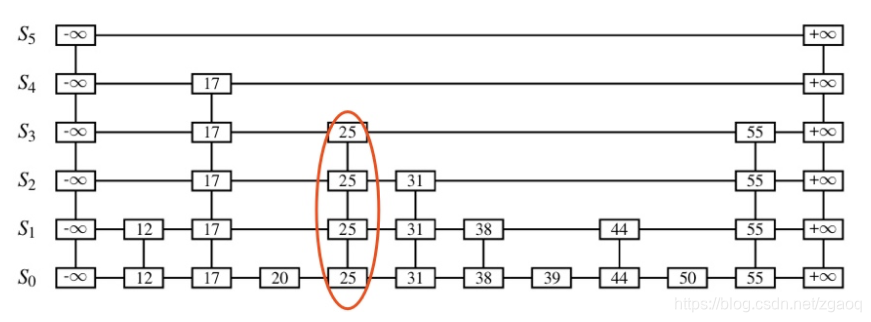
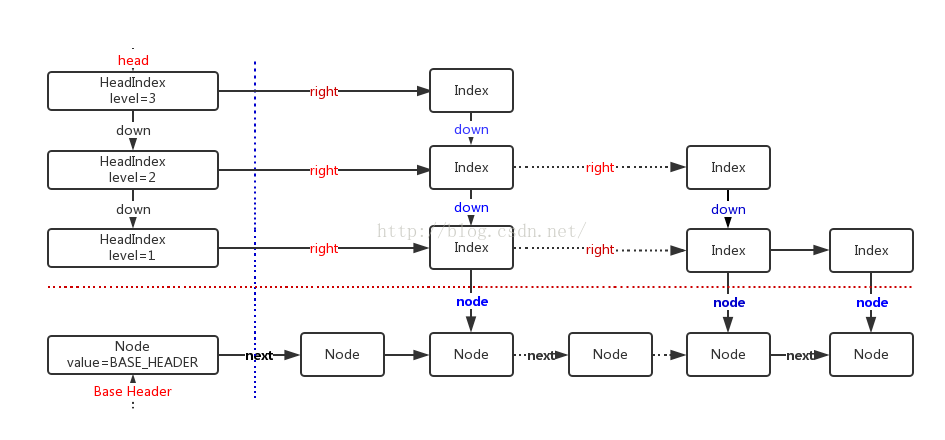
下面看一个具体的例子：
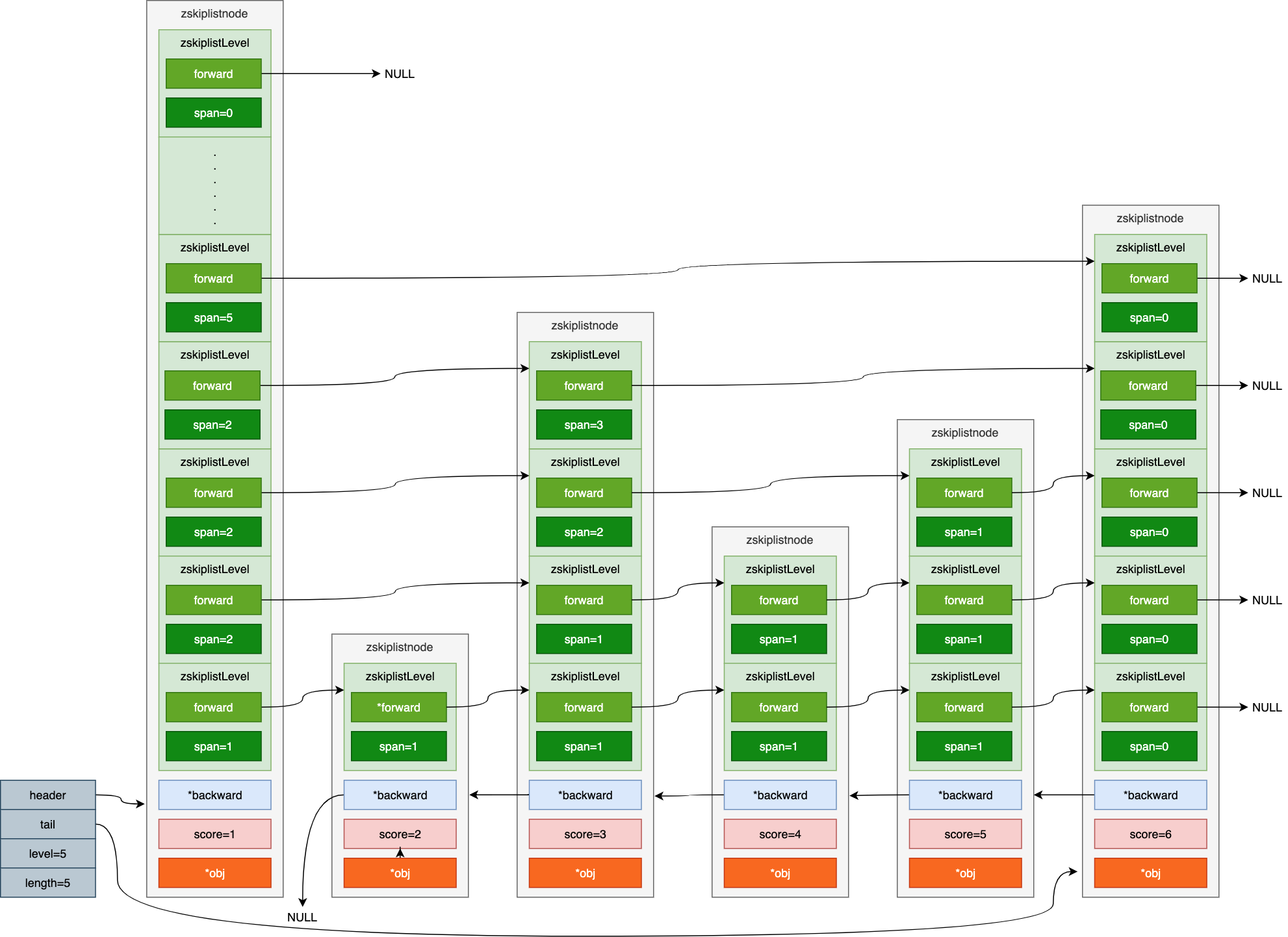
skiplist

1. 查找过程

具体代码可以见:src/t_zset.c

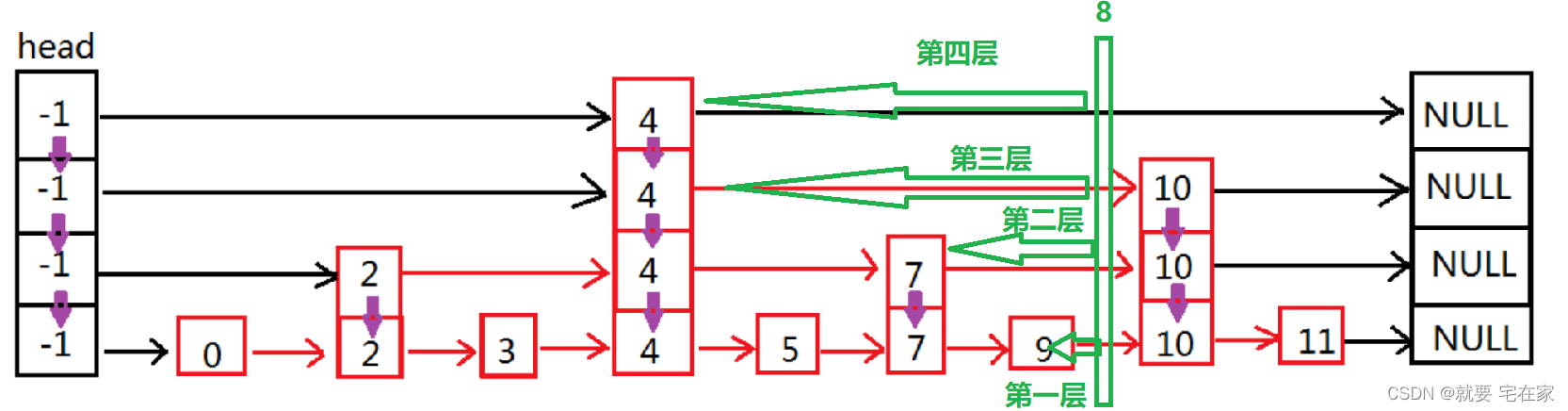
假设要找score为5的元素。
（1）首先从头结点的最高层（也就是64层）开始查找，但是由于头指针中保存了当前跳表的最高层数，所以直接从头结点的level层开始查找即可。如果zkiplistLevel的forward为NULL，则继续向下。
（2）直到头结点中第5层的zskiplistLevel的forward不为空，它指向了第6个节点的第5层，但是这个节点的score为6，大于5，所以还要从头结点向低层继续查找。
（3）头结点中第4层的zskiplistLevel的forward指向第3个节点的第4层，这个节点的score为3，小于5，并且第一个节点的span=2，这个span的作用就是用来累加并计算最终目标节点的排名的。继续从这个节点的forward向后遍历。它的forward指向第6个节点的第4层，这个节点的score为6，大于5，所以还要从前一个score为3的节点向低层继续查找。
（4）第3个节点第3层的zskiplistLevel的forward指向第5个节点的第3层，而它的score正好为5，查找成功。并且第3个节点的span=2，再加上原来的span=2等于4，所以目标节点5的排名是4。

find
结合代码来看：

unsigned long zslGetRank(zskiplist *zsl, double score, sds ele) {zskiplistNode *x;unsigned long rank = 0;int i;// 从头结点开始x = zsl->header;// 从最高层开始，向下for (i = zsl->level-1; i >= 0; i--) {while (x->level[i].forward && // 如果forward指针不为空(x->level[i].forward->score < score || // 并且如果下一个节点的分数小于目标分数或者（下一个节点的分数等于目标分数并且元素值不同）(x->level[i].forward->score == score &&sdscmp(x->level[i].forward->ele,ele) <= 0))) { rank += x->level[i].span; // rank值加上当前第i层级该位置x节点的span值x = x->level[i].forward; // 切换到该层的下一个节点}/* x might be equal to zsl->header, so test if obj is non-NULL */if (x->ele && sdscmp(x->ele,ele) == 0) {return rank;}}return 0;
}

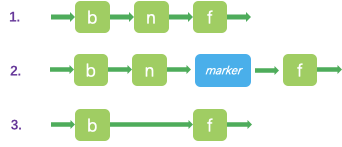
2. 插入过程

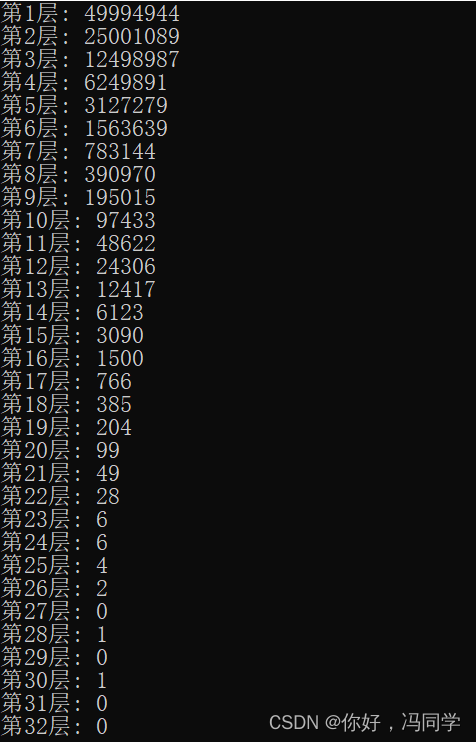
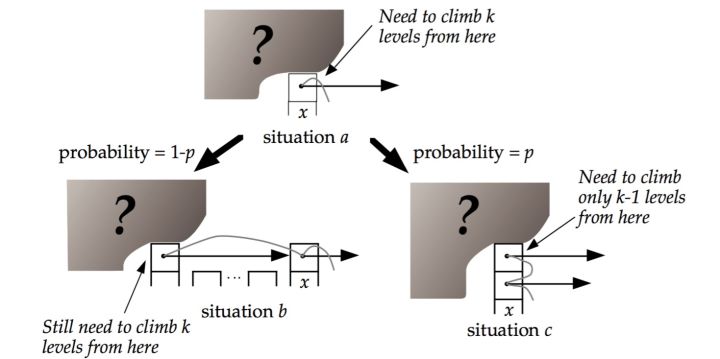
（1）首先，插入结点时，都会随机为新的节点分配一个小于64的层数，并且层数越小概率越大，层数越高概率越小。
（2）查找到小于待插入score的分数值中最大的那个节点，如果score相等，则通过value比较。
（3）在找到的节点后面插入新的节点。同时更新前面节点的跨度和跳表最大层高。
（4）更新新节点的各层的forward以及backward指针。

/* * 插入过程*/
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;unsigned int rank[ZSKIPLIST_MAXLEVEL];int i, level;serverAssert(!isnan(score));x = zsl->header;for (i = zsl->level-1; i >= 0; i--) {/* store rank that is crossed to reach the insert position */rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];while (x->level[i].forward &&(x->level[i].forward->score < score ||(x->level[i].forward->score == score &&sdscmp(x->level[i].forward->ele,ele) < 0))){rank[i] += x->level[i].span;x = x->level[i].forward;}//在i层找到合适的位置之后赋值给update[i]update[i] = x;}//随机为新的节点分配一个小于64的层数，并且层数越小概率越大，层数越高概率越小。level = zslRandomLevel();if (level > zsl->level) {//如果leveld大于当前最高层级，在leveld到zsl->levelzh之间再插入新的层级。for (i = zsl->level; i < level; i++) {rank[i] = 0;update[i] = zsl->header;update[i]->level[i].span = zsl->length;}zsl->level = level;}// 创建新的节点x = zslCreateNode(level,score,ele);for (i = 0; i < level; i++) {// 对于x节点的每一层更，更新它的forward指针和span值x->level[i].forward = update[i]->level[i].forward;update[i]->level[i].forward = x;x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);update[i]->level[i].span = (rank[0] - rank[i]) + 1;}/* increment span for untouched levels */for (i = level; i < zsl->level; i++) {update[i]->level[i].span++;}x->backward = (update[0] == zsl->header) ? NULL : update[0];if (x->level[0].forward)x->level[0].forward->backward = x;elsezsl->tail = x;zsl->length++;return x;
}/* * 返回一个随机的层级*/
int zslRandomLevel(void) {int level = 1;while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))level += 1;return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

3. 删除过程

（1）找到待删除的节点，删除节点，更新前面节点的跨度和跳表最大层高。
（2）更新新节点的各层的forward以及backward指针。

4. 修改过程

Redis中的做法比较简单，先找到待修改的节点，直接删除，然后插入修改后的新的节点。

二、SkipList与平衡树、哈希表的比较

1. 和哈希表的比较

SkipList和各种平衡树（如AVL、红黑树等）的元素是有序排列的，而哈希表不是有序的。因此，在哈希表上只能做单个key的查找，不适宜做范围查找。所谓范围查找，指的是查找那些大小在指定的两个值之间的所有节点。

2. 和平衡树的比较

在做范围查找的时候，平衡树比skiplist操作要复杂。在平衡树上，我们找到指定范围的小值之后，还需要以中序遍历的顺序继续寻找其它不超过大值的节点。如果不对平衡树进行一定的改造，这里的中序遍历并不容易实现。而在skiplist上进行范围查找就非常简单，只需要在找到小值之后，对第1层链表进行若干步的遍历就可以实现。

平衡树的插入和删除操作可能引发子树的调整，逻辑复杂，而skiplist的插入和删除只需要修改相邻节点的指针，操作简单又快速。

从内存占用上来说，skiplist比平衡树更灵活一些。一般来说，平衡树每个节点包含2个指针（分别指向左右子树），而skiplist每个节点包含的指针数目平均为1/(1-p)，具体取决于参数p的大小。如果像Redis里的实现一样，取p=1/4，那么平均每个节点包含1.33个指针，比平衡树更有优势。

查找单个key，skiplist和平衡树的时间复杂度都为O(log n)，大体相当；而哈希表在保持较低的哈希值冲突概率的前提下，查找时间复杂度接近O(1)，性能更高一些。所以我们平常使用的各种Map或dictionary结构，大都是基于哈希表实现的。

从算法实现难度上来比较，skiplist比平衡树要简单得多。

THE END.


http://chatgpt.dhexx.cn/article/3e7DBdE4.shtml

相关文章

skiplist原理与实现

skiplist原理与实现

今天继续介绍分布式系统当中常用的数据结构&#xff0c;今天要介绍的数据结构非常了不起&#xff0c;和之前介绍的布隆过滤器一样&#xff0c;是一个功能强大原理简单的数据结构。并且它的缺点和短板更少&#xff0c;应用更加广泛&#xff0c;比如广泛使用的Redis就有用到它。 …
阅读更多...
【数据结构】跳表Skiplist

【数据结构】跳表Skiplist

文章目录 跳表--skiplistskiplist的概念skilplist的原理skilplist的实现随机值函数跳表节点 跳表框架查找函数寻找前置节点添加元素删除元素打印链表 测试结果Skiplist与其他Key-Value结构的比较 跳表–skiplist skiplist的概念 skiplist本质上也是一种查找结构&#xff0c;用…
阅读更多...
Skiplist跳表详解及其模拟实现

Skiplist跳表详解及其模拟实现

文章目录 跳表1.跳表的概念2.Skiplist在插入时采用随机层数的方法是如何保证效率的呢?3.跳表的模拟实现4.跳表VS平衡搜索树和哈希表 跳表 1.跳表的概念 跳表是基于有序链表扩展实现的。对于一个普通的有序链表&#xff0c;我们查找数据的时间复杂度是O(N)。而跳表的出现&…
阅读更多...
skiplist - 跳表

skiplist - 跳表

一 前言 跳表(skiplist、跳跃表) 是一个很优秀的数据结构&#xff0c;比如用于 Redis、levelDB等出名的开源项目上。跳表在原有的有序链表上面增加了多级索引&#xff0c;通过索引来实现快速查找。 它的结构特点在名称能很好的体现出来&#xff0c;就像兔子一样&#xff0c;蹦…
阅读更多...
Leveldb skiplist 实现及解析

Leveldb skiplist 实现及解析

skiplist 原理介绍 skiplist 由William Pugh 在论文Skip Lists: A Probabilistic Alternative to Balanced Trees 中提出的一种数据结构，skiplist 是一种随机化存储的多层线性链表结构，插入，查找，删除的都是对数级别的时间复杂度。skiplist 和平衡树有相同的时间复杂度，但…
阅读更多...
跳表SkipList介绍与实现

跳表SkipList介绍与实现

目录 一.跳表介绍 二.实现思路 &#xff08;一&#xff09;.结点结构 &#xff08;二&#xff09;.检索 &#xff08;三&#xff09;.插入 &#xff08;四&#xff09;.删除 三.实现代码 一.跳表介绍 跳表是一种随机化数据结构&#xff0c;主要用于快速检索数据。实质上…
阅读更多...
SkipList(跳表)

SkipList(跳表)

SkipList(跳表) 文章目录 SkipList(跳表)参考前言跳表的原理跳表的插入和删除插入操作删除操作 跳表的时间空间复杂度分析时间复杂度空间复杂度 调表的基本操作插入数据删除数据 Go 实现小结 参考 https://juejin.cn/post/6844903955831619597#heading-2https://blog.csdn.net…
阅读更多...
每日一博 - 如何理解跳表(SkipList)

每日一博 - 如何理解跳表(SkipList)

文章目录 什么是跳跃表SkipList跳表关键字Why Skip ListCode跳表-查询跳表-删除跳表-插入 小结完整Code 什么是跳跃表SkipList 跳跃表(简称跳表)由美国计算机科学家William Pugh于1989年发明 论文&#xff1a; Skip lists: a probabilistic alternative to balanced trees 跳…
阅读更多...
Skiplist（跳表）实现

Skiplist（跳表）实现

前言&#xff1a;跳表本质是一种查找结构&#xff0c;相较于AVL树、红黑树、哈希表&#xff0c;实现起来要更加简单&#xff0c;而且效率也不差。 一.Skiplist概念 跳表本质也是一种查找结构&#xff0c;用于解决算法中的查找问题&#xff0c;跟平衡搜索树&#xff08;AVL树、红…
阅读更多...
跳表(SkipList)设计与实现(java)

跳表(SkipList)设计与实现(java)

微信搜一搜「bigsai」关注这个有趣的程序员&#xff0c;一起做个朋友 新人原创公众号&#xff0c;求支持一下&#xff01;你的点赞三连肯定对我至关重要&#xff01; 文章已收录在 我的Github bigsai-algorithm 欢迎star 前言 跳表是面试常问的一种数据结构&#xff0c;它在很…
阅读更多...
SkipList和java中ConcurrentSkipListMap的实现

SkipList和java中ConcurrentSkipListMap的实现

文章目录 简介SkipListConcurrentSkipListMapSkipList的实现concurrent的实现 总结 SkipList和java中ConcurrentSkipListMap的实现 简介 一开始听说SkipList我是一脸懵逼的&#xff0c;啥&#xff1f;还有SkipList&#xff1f;这个是什么玩意。 后面经过我的不断搜索和学习&a…
阅读更多...
跳表（SkipList）及ConcurrentSkipListMap源码解析

跳表（SkipList）及ConcurrentSkipListMap源码解析

二分查找和AVL树查找 二分查找要求元素可以随机访问&#xff0c;所以决定了需要把元素存储在连续内存。这样查找确实很快&#xff0c;但是插入和删除元素的时候&#xff0c;为了保证元素的有序性&#xff0c;就需要大量的移动元素了。 如果需要的是一个能够进行二分查找&#…
阅读更多...
Redis数据结构之——跳表skiplist

Redis数据结构之——跳表skiplist

写在前面 以下内容是基于Redis 6.2.6 版本整理总结 一、跳表&#xff08;skiplist&#xff09; 如何理解跳表&#xff1f;在了解跳表之前&#xff0c;我们先从普通链表开始&#xff0c;一点点揭开跳表的神秘面纱~ 首先&#xff0c;普通单链表来说&#xff0c;即使链表是有序…
阅读更多...
redis中ziplist，skiplist

redis中ziplist，skiplist

ziplist压缩表 ziplist主要是为了节约内存&#xff0c;他将元素存储在一块连续的内存空间中&#xff0c;这样在查询数据的时候也可以利用CPU的缓存访问数据&#xff0c;加快查询的效率 相较于数组而言。我们知道,数组要求每个元素的大小都相同,如果我们要存储不同长度的字符串…
阅读更多...
跳表-skiplist的简单实现

跳表-skiplist的简单实现

文章目录 1、什么是跳表-skiplist2、skiplist的效率如何保证&#xff1f;3、skiplist的实现4、skiplist跟平衡搜索树和哈希表的对比 1、什么是跳表-skiplist skiplist本质上也是一种查找结构&#xff0c;用于解决算法中的查找问题&#xff0c;跟平衡搜索树和哈希表的价值是一样…
阅读更多...
跳表:Skiplist原理介绍和优缺点

跳表:Skiplist原理介绍和优缺点

skiplist介绍 不要求上下相邻两层链表之间的节点个数有严格的对应关系&#xff0c;而是为每个节点随机出一个层数(level)。比如&#xff0c;一个节点随机出的层数是3&#xff0c;那么就把它链入到第1层到第3层这三层链表中。为了表达清楚&#xff0c;下图展示了如何通过一步步的…
阅读更多...
skiplist 跳跃表详解及其编程实现

skiplist 跳跃表详解及其编程实现

skiplist介绍 跳表(skip List)是一种随机化的数据结构&#xff0c;基于并联的链表&#xff0c;实现简单&#xff0c;插入、删除、查找的复杂度均为O(logN)。跳表的具体定义&#xff0c; 请参考参考维基百科 点我&#xff0c;中文版。跳表是由William Pugh发明的&#xff0c;这…
阅读更多...
浅析SkipList跳跃表原理及代码实现

浅析SkipList跳跃表原理及代码实现

转载请注明&#xff1a;http://blog.csdn.net/ict2014/article/details/17394259 SkipList在leveldb以及lucence中都广为使用&#xff0c;是比较高效的数据结构。由于它的代码以及原理实现的简单性&#xff0c;更为人们所接受。我们首先看看SkipList的定义&#xff0c;为什么叫…
阅读更多...
跳表（skiplist）的理解

跳表（skiplist）的理解

听到跳表（skiplist）这个名字，既然是list，那么应该跟链表有关。 跳表是有序链表，但是我们知道，即使对于排过序的链表，我们对于查找还是需要进行通过链表的指针进行遍历的，时间复杂度很高依然是O(n)，这个显然是不能接受的。是否可以像数组那样，通过二分法进行查找呢，但…
阅读更多...
SkipList详解

SkipList详解

本文参考&#xff1a;《大数据日知录》 概念 SkipList是一种用来代替平衡树的数据结构。 虽然在最坏的情况下SkipList的效率要低于平衡树&#xff0c;但是大多数情况下效率仍然非常高&#xff0c;其插入、删除、查找的时间复杂度都是O(log(N))。 除了高效外&#xff0c;其实现…
阅读更多...
推荐文章

Copyright @ 2022~2023