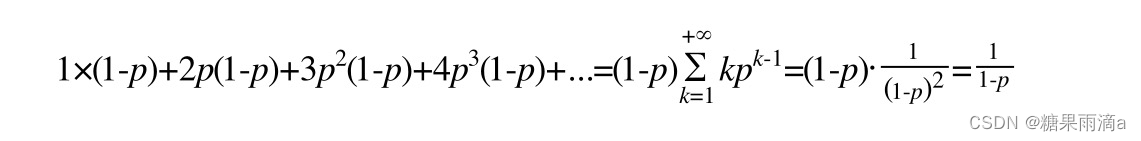SkipList(跳表)

参考

• https://juejin.cn/post/6844903955831619597#heading-2
• https://blog.csdn.net/qq_56999918/article/details/122960821
• 王争老师的SkipList实现

前言

下文介绍一种基于单链表的高级数据结构，跳表。

将单链表先进行排序，然后针对有序链表为了实现高效的查找，可以使用跳表这种数据结构。其根本思想是二分查找的思想。

跳表的前提条件是针对有序的单链表，实现高效地查找，插入、删除。

Redis中的，有序集合sorted set就是用跳表实现的。

跳表的原理

对于单链表，就是是存储的有序数据（即 有序链表上），想在其中查找某个数据，也只能从头到尾遍历，查找效率低，时间复杂度是O(n),如下图所示：

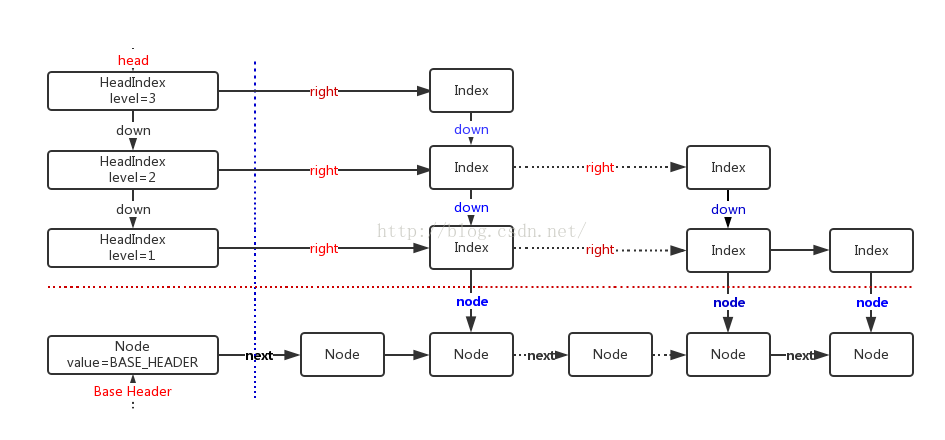
为了提高查找效率，并使用二分查找的思想，我们对有序链表建立了一级“索引”。每两个节点提取一个节点到索引层。索引层中的每个节点都包含两个指针，一个指向下一个节点，一个down指针，指向下一级节点。

例如我们需要查找图中7 这个节点：

通过有序链表我们需要5次才能查找到，而对于类似上图加上以及索引的结构时我们只需要查找3次就可以找到7这个节点。

那么查找的次数能否再减少呢？我们会很自然想到可以与一级索引类似的再添加一层二级索引，如下图：

还是同样去查找7这个节点我们发现，只需遍历两个节点便可以查找到7这个节点了。

通过建立索引的方式，对于数据量越大的有序链表，通过建立多级索引，查找效率提升会非常明显。这种链表加多级索引的结构就是跳表。

对于查找离链首的节点效果可能不会很明显，对于距离链首越远的节点跳表提升的性能会更明显。

跳表的插入和删除

对于链表类数据结构的插入删除操作的时间复杂度为O(log n)(对于链表类的数据结构插入删除的时间复杂度一般与查找的时间复杂度保持一致).

插入操作

为了保证原始链表中的数据的有序性，我们需要先找到新数据应该插入的位置。可以基于多级索引，快速查找到新数据的插入位置，时间复杂度为(log n).

假设插入数据为6的节点，如下图：

删除操作

删除原链表中的节点，如果节点存在于索引中，也要删除索引中的节点。因为单链表中的删除需要用到要删除节点的前驱节点。可以像插入操作一样，通过索引逐层向下遍历到原始链表中，要删除的节点，并记录其前驱节点，从而实现删除操作。

跳表的时间空间复杂度分析

时间复杂度

在讨论跳表查找的时间复杂度前我们先来讨论一下跳表的索引高度。若按照两个节点会多出一个节点作为上级索引节点的话，不难想到跳表有$h=lo{g}_{2}n$层。

接下来我们跟着上图中用红色加粗的线去看一下一个跳表查询的路径。我们可以发现每层索引最多遍历3个元素。此时我们还知道跳表的高度$h=lo{g}_{2}n$，所以跳表中查找一个元素的时间复杂度为$O(3\ast logn)$,忽略常数即为：$O(logn)$.

空间复杂度

跳表提升元素查找效率的思想就是典型的"空间换时间"的思想。

索引建立的策略仍按照两个节点会多出一个节点作为上级索引节点(前提)。假如原始链表包含n个元素，则一级索引元素个数为$n/2$、二级索引元素个数为$n/4$依次类推。所以索引节点数就是一个等比数列的求和:$n/2+n/4+....+2=n-2$

，空间复杂度是O(n).

可以注意到我们在前面计算空间复杂度时是有前提的，如果我们现在按照每三个节点抽一个节点作为索引，计算方式类似的我们可以推出索引节点的总和是：$n/3+n/9+...+3=n/2$,减少了一般。所以我们可以通过减少索引来减少空间复杂度，不过与此同时会降低查找的效率。

调表的基本操作

插入数据

我们可以将在跳表中插入数据动作分成两个部分：

1. 查找到插入的位置

   类似于查找，跳表中数据结构是有序的。这一步中我们要找的就是前一个元素比待插入元素X小后一个元素比待插入元素X大的那个位置。

2. 更新索引

   层级索引其实是跳表中的核心。如果我们一直往原始列表中插入数据，但是不更新索引，那么会出现两个索引系欸但之间数据非常多的情况，极端情况下跳表将退化为单链表.因此我们需要一个索引更新策略。

   索引更新策略

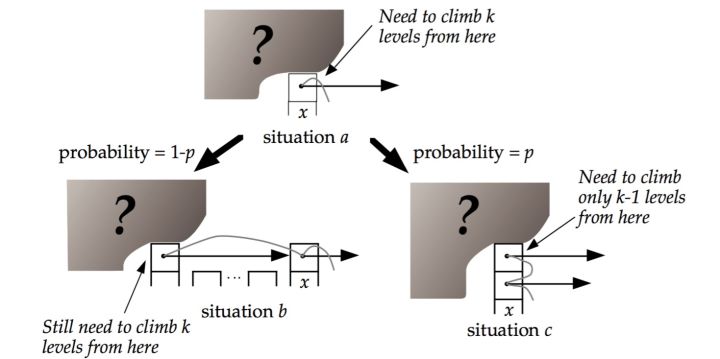
   假如跳表每一层的晋升概率为1/2，最理想的索引就是在原始链表中每隔一个元素抽取一个元素作为一级索引。那么我们是否可以在原始链表中随机选取n/2个元素作为一级索引是否也能达到一样的效果呢？实际上是可以的，因为好数据结构都是为了应对大数据量的场景，当原始链表中的元素数量足够多，我们得到的索引也会是比较均匀的。因此，我们可以使用这样一个索引策略：随机选取n/2个元素作为一级索引、随机选n/4，以此类推，一直到最顶层的索引。

   我们可以先来看看代码：

   // 向跳表中插入数据
   func (list *SkipListInt) Set(key int64, value interface{}) {list.mutex.Lock()defer list.mutex.Unlock()prev := &list.SkipNodeIntvar next *SkipNodeIntfor i := list.level - 1; i >= 0; i-- {next = prev.next[i]for next != nil && next.key < key {prev = nextnext = prev.next[i]}// 记录查找过来的路径list.update[i] = prev}// 如果key已经存在if next != nil && next.key == key {next.value = valuereturn}// 随机生成新节点的层数level := list.randomLevel()if level > list.level {level = list.level + 1list.level = levellist.update[list.level-1] = &list.SkipNodeInt}// 申请新的节点node := &SkipNodeInt{}node.key = keynode.value = valuenode.next = make([]*SkipNodeInt, level)// 根据前面查找到的这个位置 向不同的层架新增索引for i := 0; i < level; i++ {node.next[i] = list.update[i].next[i]list.update[i].next[i] = node}list.length++
   }
   

   这部分代码就是按照前面提到的两步去插入数据的。其中这个list.randomLevel()的作用就是随机获得要插入数据要更新的索引层级(其概率分布是一级索引1/2, 二级索引1/4 ……)。这里应该可以大致理解维护索引的这个策略了。下面我们通过一个例子更加清晰的去看插入数据的过程。

   例如我们需要在跳表中插入数据6，首先 randomLevel() 返回了3，表示需要建立3级索引。

   

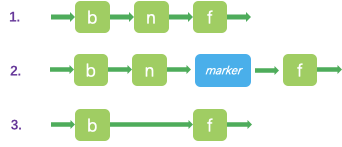
通过上图我们可以比较清晰地看到整个数据插入、索引更新的过程。绘制的这系列图其实展现了一种实现的思路：

1. 获得需更新的索引层级
2. 找到待插入元素的索引区间，就向这个索引区间中插入这个元素

当然我们也可以先找到元素需要插入的位置，在过程中记录查找的路径（最后给出的代码按照这种思路）。

删除数据

跳表删除数据时需要把索引中对应的节点都删掉。如下图中，要删除元素9，我们需要对原始链表一级一级索引中的9都删除掉。

这里我不做详解，思路其实与在调表中查找数据的方式一致。不同的是不能在索引层级查找时就退出，而需要继续深入到原始链表。这样子可以找到跳表的所有层级索引中与待删除元素直接相连的前一个元素。

Go 实现

package mainimport ("math/rand""sync""time"
)// 跳表的节点
type SkipNodeInt struct {key   int64value interface{}next  []*SkipNodeInt
}// 跳表的结构
type SkipListInt struct {SkipNodeIntmutex  sync.RWMutexupdate []*SkipNodeIntrand   *rand.Randmaxl   intskip   intlevel  intlength int
}// 初始化一个跳表
func NewSkipListInt(skip ...int) *SkipListInt {list := &SkipListInt{}list.maxl = 32list.skip = 4list.level = 0list.length = 0list.SkipNodeInt.next = make([]*SkipNodeInt, list.maxl)list.update = make([]*SkipNodeInt, list.maxl)list.rand = rand.New(rand.NewSource(time.Now().UnixNano()))if len(skip) == 1 && skip[0] > 1 {list.skip = skip[0]}return list
}// 查找跳表中的元素
func (list *SkipListInt) Get(key int64) interface{} {list.mutex.Lock()defer list.mutex.Unlock()prev := &list.SkipNodeIntvar next *SkipNodeInt// 先从最高层的调表去查找for i := list.level - 1; i >= 0; i-- {next = prev.next[i]// 同级索引查找 如果找到的还是比给定的key小的话就跳到下一个点继续查找for next != nil && next.key < key {prev = nextnext = prev.next[i]}// 找到对应的元素就退出查找if next != nil && next.key == key {return next.value}}return nil
}// 向跳表中插入数据
func (list *SkipListInt) Set(key int64, value interface{}) {list.mutex.Lock()defer list.mutex.Unlock()prev := &list.SkipNodeIntvar next *SkipNodeIntfor i := list.level - 1; i >= 0; i-- {next = prev.next[i]for next != nil && next.key < key {prev = nextnext = prev.next[i]}// 记录查找过来的路径list.update[i] = prev}// 如果key已经存在if next != nil && next.key == key {next.value = valuereturn}// 随机生成新节点的层数level := list.randomLevel()if level > list.level {level = list.level + 1list.level = levellist.update[list.level-1] = &list.SkipNodeInt}// 申请新的节点node := &SkipNodeInt{}node.key = keynode.value = valuenode.next = make([]*SkipNodeInt, level)// 根据前面查找到的这个位置 向不同的层架新增索引for i := 0; i < level; i++ {node.next[i] = list.update[i].next[i]list.update[i].next[i] = node}list.length++
}// 调表中移除某个元素
func (list *SkipListInt) Remove(key int64) interface{} {list.mutex.Lock()defer list.mutex.Unlock()prev := &list.SkipNodeIntvar next *SkipNodeInt// 这种查找方式保证查到路径一定会经过底层的索引，这为后面删除元素时更新索引提供了遍历// 查找时可以找到对应的key时就直接推出for i := list.level - 1; i >= 0; i-- {next = prev.next[i]for next != nil && next.key < key {prev = nextnext = prev.next[i]}list.update[i] = prev}// 节点不存在node := nextif next == nil || next.key != key {return nil}// 调整next的指向for i, v := range node.next {if list.update[i].next[i] == node {list.update[i].next[i] = vif list.SkipNodeInt.next[i] == nil {list.level -= 1}}list.update[i] = nil}list.length--return node.value
}// 获得跳表的长度
func (list *SkipListInt) GetLength() int {list.mutex.Lock()defer list.mutex.Unlock()return list.length
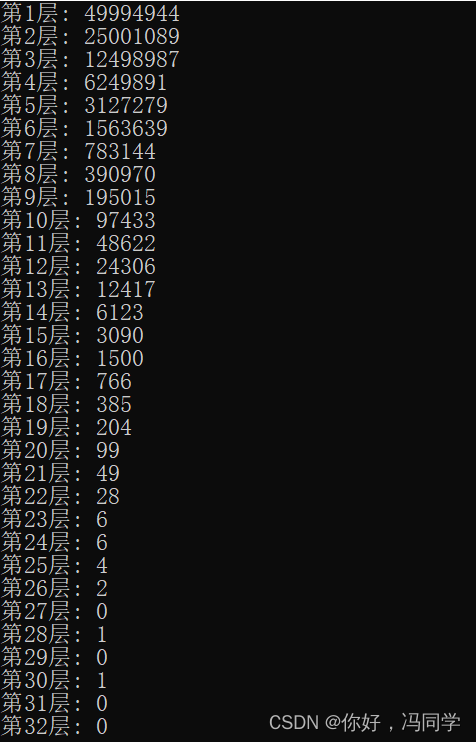
}// 随机生成位于第几层调表
func (list *SkipListInt) randomLevel() int {i := 1for ; i < list.maxl; i++ {if list.rand.Int31()%int32(list.skip) != 0 {break}}return i
}

小结

• 跳表通过时间换空间的方式实现了可二分查找的有序链表
• 跳表查询、插入、删除的时间复杂度都为O(log n)，与平衡二叉树接近