文章目录
- 常见的概念
- 信号的描述
- 信号的分类
- 确定信号和随机信号
- 连续信号和离散信号
- 周期信号和非周期信号
- 能量信号和功率信号
- 一维信号和多维信号
- 因果信号和非因果信号
- 信号的matlab表示与绘图
常见的概念
- 消息,来自外界的各种报道统称为消息
- 信息,消息中有意义的内容称为信息
事件中所含信息量的计算公式:
I = l o g 2 P ( x ) I=log_2{P(x)} I=log2P(x)
P ( x ) P(x) P(x)代表事件发生的概率, I I I表示信息量,单位是bit - 信号,信息的载体,声信号、光信号、无线电信号等
信号的描述
两种方法描述信号:
- 时间的函数
- 波形
信号的分类
确定信号和随机信号
- 确定性信号,任意时刻的取值都是确定的信号
- 随机信号,任意时刻的取值都具有不确定性,比如热噪声
连续信号和离散信号
- 连续信号,在连续的时间范围内都有定义的信号(有时也叫模拟信号)
- 离散信号,只有在离散的瞬间才有定义的信号
- 离散序列,等间隔的离散信号(离散序列简称
序列)
注意:
离散信号中的离散,指的是信号的定义域,也就是时间是离散的,并未要求取值是离散的,当取值是离散的时候,就是我们所说的数字信号
周期信号和非周期信号
- 周期信号,每隔一定时间,按同样的规律重复变化的信号
连续周期信号:
f ( t ) = f ( t + m T ) , m = 0 , ± 1 , ± 2 , . . . f(t)=f(t+mT) ,m=0,\pm1,\pm2,... f(t)=f(t+mT),m=0,±1,±2,...
离散周期信号:
f ( k ) = f ( k + m N ) , m = 0 , ± 1 , ± 2 , . . . f(k)=f(k+mN) ,m=0,\pm1,\pm2,... f(k)=f(k+mN),m=0,±1,±2,...
满足上述关系的最小的T或整数N,就是周期
若,两个周期信号的周期之比为有理数(分子分母均为整数),则两个信号相加仍为周期信号 - 非周期信号
不满足上述关系的就是非周期信号
若,两个周期信号的周期之比为无理数理数,则两个信号相加为非周期信号
注意:
连续正弦信号一定是周期信号,而正弦序列不一定是周期序列
两个连续周期信号之和不一定是周期信号,但两个周期序列之和一定是周期序列
能量信号和功率信号
能量有限的叫能量信号,功率有限的叫功率信号
将 f ( t ) 将f(t) 将f(t)看做是电压或电流,施加在1欧姆的电阻上,则消耗的瞬时功率 P ( t ) = ∣ f ( t ) ∣ 2 P(t)=|f(t)|^2 P(t)=∣f(t)∣2
信号的能量:
E = ∫ − ∞ ∞ ∣ f ( t ) ∣ 2 d t E=\int_{-\infty}^{\infty}|f(t)|^2dt E=∫−∞∞∣f(t)∣2dt
信号的功率:
P = lim t → ∞ 1 T ∣ f ( t ) ∣ 2 d t P=\lim \limits_{t \to \infty}\frac{1}{T}|f(t)|^2dt P=t→∞limT1∣f(t)∣2dt
一维信号和多维信号
- 一维信号:一个变量的函数,比如:语音信号随时间变化的函数
- 二维信号;多个变量的函数,比如:图像
这里的维,指的是变量的个数
因果信号和非因果信号
- 因果信号: t = 0 t=0 t=0时接入系统的信号 f ( t ) f(t) f(t), t < 0 t<0 t<0时, f ( t ) = 0 f(t)=0 f(t)=0
- 非因果信号: t ≥ 0 t \ge 0 t≥0时, f ( t ) = 0 f(t)=0 f(t)=0
信号的matlab表示与绘图
连续信号
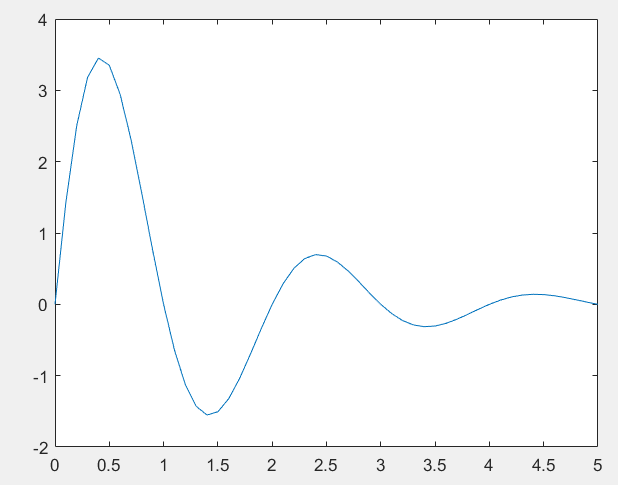
画出 f ( t ) = 5 ∗ e − 0.8 ∗ t s i n ( p i ∗ t ) , 0 < t < 5 f(t)=5*e^{-0.8*t}sin(pi*t),0<t<5 f(t)=5∗e−0.8∗tsin(pi∗t),0<t<5的图像
t=0:0.1:5;
y=5*exp(-0.8*t).*sin(pi*t);
plot(t,y)
离散信号
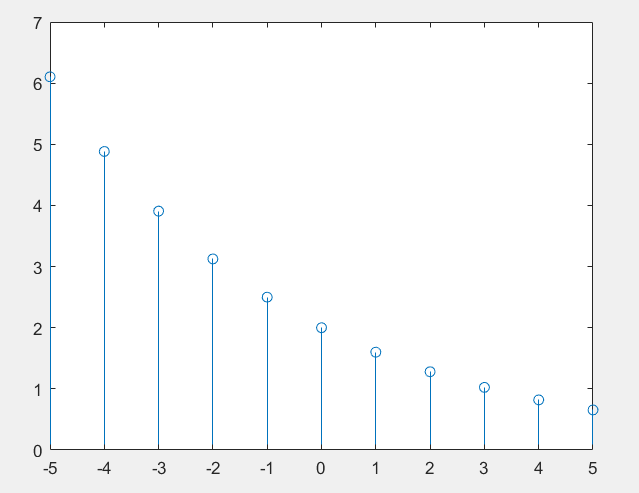
画出 y = 2 ( 0.8 ) k , − 5 < k < 5 y=2(0.8)^k,-5<k<5 y=2(0.8)k,−5<k<5
k=-5:1:5;
y=2*(0.8).^k;
stem(k,y)