文章目录
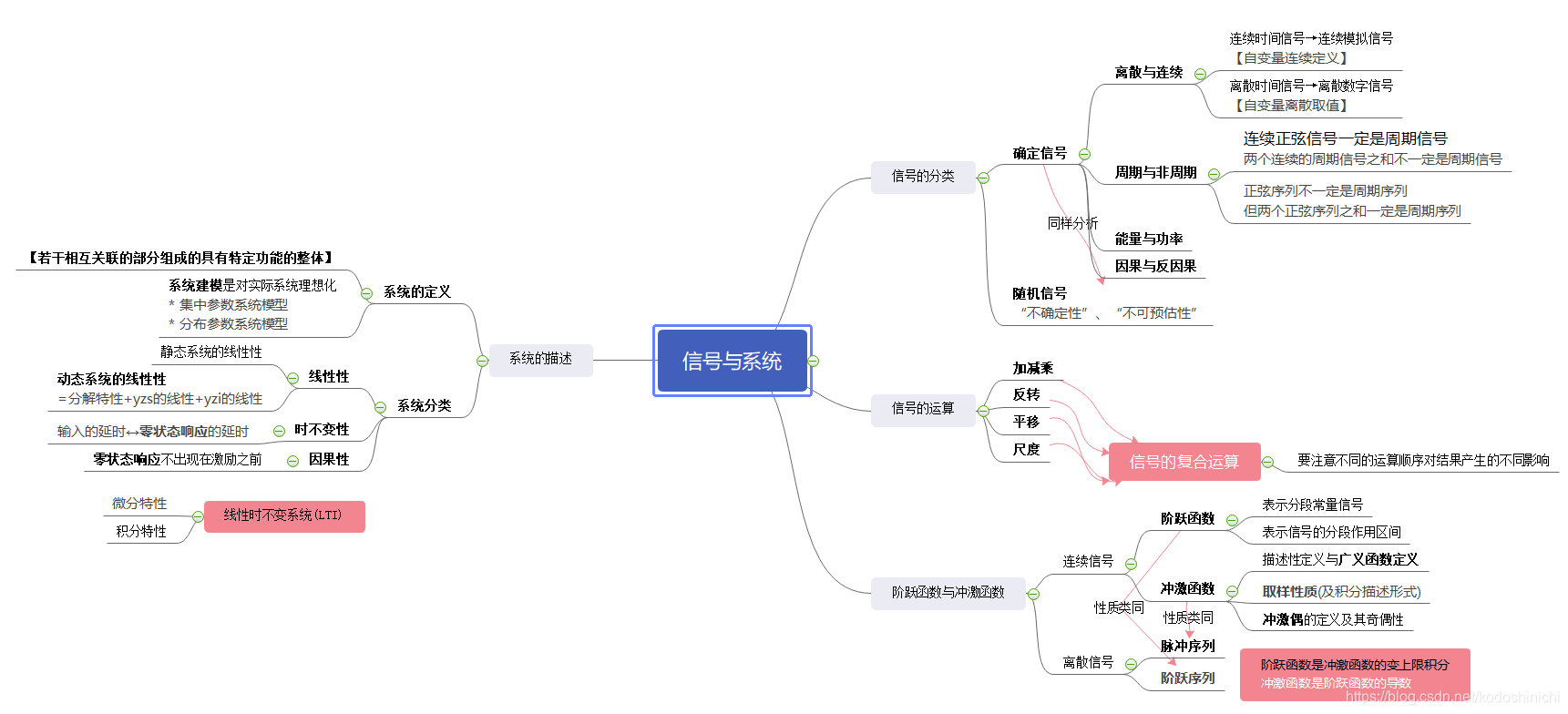
- 第一章 信号与系统概述
- 1.4 系统的概念及分类
- 1.4.1 系统定义与典型系统举例
- 1.4.1.1 系统定义
- 1.4.1.2 系统模型
- 1.4.1.3 系统的状态
- 1.4.1.4 典型系统举例
- 1.4.2 系统分类
- 1.4.2.1 连续系统与离散系统
- 1.4.2.2 动态系统与即时系统
- 1.4.2.3 单输入单输出系统与多输入多输出系统
- 1.4.2.4 线性系统与非线性系统
- 1.4.2.4.1 线性性质
- 1.4.2.4.2 动态线性系统的判定条件
- 1.4.2.5 时变系统与时不变系统
- 1.4.2.5.1 时不变性质
- 1.4.2.5.2 时不变的直观判断方法
- 1.4.2.5.3 LTI连续系统的微分特性和积分特性
- 1.4.2.6 因果与非因果系统
- 1.4.2.7 稳定系统与不稳定系统
第一章 信号与系统概述
1.4 系统的概念及分类
1.4.1 系统定义与典型系统举例
1.4.1.1 系统定义
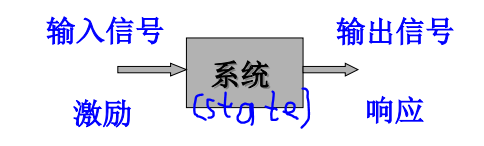
系统(system):是指若干相互关联的事物组合而成,具有特定功能的整体。 表示如下:

系统的基本作用:对输入信号进行加工和处理,将其转换为所需要的输出信号。
1.4.1.2 系统模型
系统模型:对实际系统的理想化。
1.4.1.3 系统的状态
定义: 系统在任意时刻 t 0 t_0 t0的状态,是指取该时刻最少数目的一组数,这组数连同 t 0 t_0 t0以后的输入足以确定 t > t 0 t>t_0 t>t0时刻的输出。 (系统具有记忆能力。系统具有历史结果)
1.4.1.4 典型系统举例
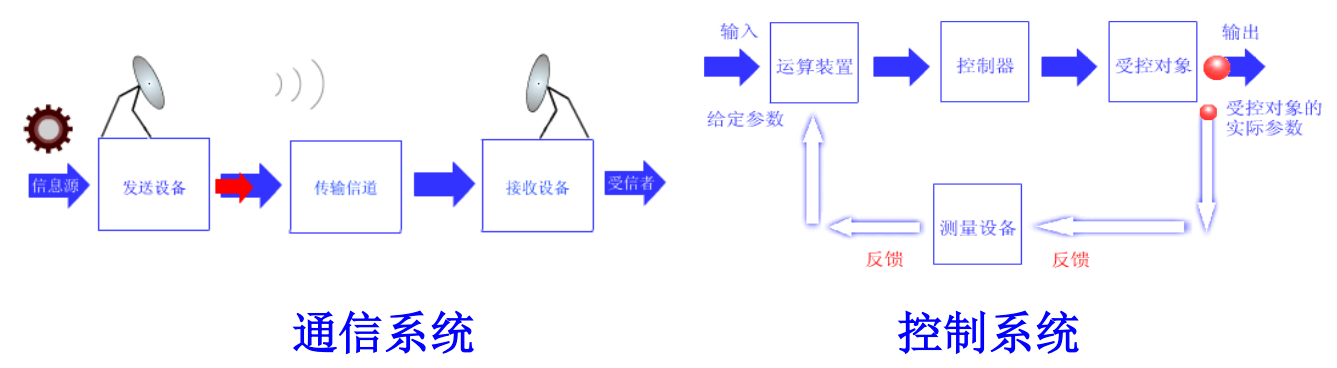
手机、电视机、通信网、计算机网等都可以看成系统,它们所传送的电波、语音、音乐、图像、文字等都可以看成信号。
1.4.2 系统分类
1.4.2.1 连续系统与离散系统
若系统的输入信号,输出信号都是连续信号,则称该系统为连续时间系统。
若系统的输入信号,输出信号都是离散信号,则称该系统为离散时间系统。
1.4.2.2 动态系统与即时系统
若系统在任一时刻的响应不仅与该时刻的激励有关,而且与它过去的历史状况有关,则称为动态系统或记忆系统。含有记忆元件(电容、电感等)的系统都是动态系统;否则称为即时系统或无记忆系统(如电阻电路)。
1.4.2.3 单输入单输出系统与多输入多输出系统
顾名思义。
1.4.2.4 线性系统与非线性系统
1.4.2.4.1 线性性质
线性系统是指满足线性性质的系统。

齐次性:
a f 1 ⟶ a y 1 a f_{1} \quad \longrightarrow \quad a y_{1} af1⟶ay1
可加性:
f 2 ⟶ y 2 f 1 + f 2 ⟶ y 1 + y 2 \begin{array}{clc}f_{2} & \longrightarrow & y_{2} \\f_{1}+f_{2} & \longrightarrow & y_{1}+y_{2}\end{array} f2f1+f2⟶⟶y2y1+y2
线性性:
a f 1 + b f 2 ⟶ a y 1 + b y 2 a f_{1}+b f_{2} \quad \longrightarrow \quad a y_{1}+b y_{2} af1+bf2⟶ay1+by2
T [ a f 1 ( ⋅ ) + b f 2 ( ⋅ ) ] = a T [ f 1 ( ⋅ ) ] + b T [ f 2 ( ⋅ ) ] T[a f_1(·) + bf_2(·)] = aT[ f_1(·)] + bT[ f_2(·)] T[af1(⋅)+bf2(⋅)]=aT[f1(⋅)]+bT[f2(⋅)]
1.4.2.4.2 动态线性系统的判定条件
动态系统的响应不仅与激励 { f ( ⋅ ) } \{ f (·) \} {f(⋅)}有关,而且与它过去的状态 { x ( 0 ) } \{x(0)\} {x(0)}有关。即系统的完全相应可分解为两部分——仅仅由输入产生的(零状态)响应和仅仅由状态产生的(零输入)响应,即具有可分解性。
-
完全响应:
y ( ⋅ ) = T [ { f ( ⋅ ) } , { x ( 0 ) } ] , f 为 输 入 , x 为 状 态 y (·) = T [\{ f(·) \},\{x(0)\}],f为输入,x为状态 y(⋅)=T[{f(⋅)},{x(0)}],f为输入,x为状态 -
零状态响应:
y z s ( ⋅ ) = T [ { f ( ⋅ ) } , { 0 } ] y_{zs}(·) = T [\{ f(·) \}, \{0\}] yzs(⋅)=T[{f(⋅)},{0}]
- 零输入响应:
y z i ( ⋅ ) = T [ { 0 } , { x ( 0 ) } ] y_{zi}(·) = T [ \{0\},\{x(0)\}] yzi(⋅)=T[{0},{x(0)}]
当动态系统满足下列三个条件时该系统为线性系统:
- 可分解性(一个响应可分解为零输入与零状态):
y ( ⋅ ) = y z s ( ⋅ ) + y z i ( ⋅ ) y (·) = y_{zs}(·) + y_{zi}(·) y(⋅)=yzs(⋅)+yzi(⋅) - 零状态线性(状态为0,输入的线性组合等于其响应的线性组合):
T [ { a f 1 ( t ) + b f 2 ( t ) } , { 0 } ] = a T [ { f 1 ( ⋅ ) } , { 0 } ] + b T [ { f 2 ( ⋅ ) } , { 0 } ] T[\{af_1(t) +bf_2(t)\}, \{0\}]=aT[\{f_1(·)\},\{0\}]+bT[\{f_2(·)\},\{0\}] T[{af1(t)+bf2(t)},{0}]=aT[{f1(⋅)},{0}]+bT[{f2(⋅)},{0}] - 零输入线性(输入为0,状态的线性组合等于其响应的线性组合):
T [ { 0 } , { a x 1 ( 0 ) + b x 2 ( 0 ) } ] = a T [ { 0 } , { x 1 ( 0 ) } ] + b T [ { 0 } , { x 2 ( 0 ) } ] T[\{0\},\{ax_1(0) +bx_2(0)\}]=aT[\{0\},\{x_1(0)\}] +bT[\{0\},\{x_2(0)\}] T[{0},{ax1(0)+bx2(0)}]=aT[{0},{x1(0)}]+bT[{0},{x2(0)}]


1.4.2.5 时变系统与时不变系统
1.4.2.5.1 时不变性质
时不变系统:系统输入延迟多少时间,其零状态响应也相应延迟多少时间。系统不随时间变化

时不变性: f ( t − t d ) ⟶ y z s ( t − t d ) f\left(t-t_{d}\right) \longrightarrow y_{z s}\left(t-t_{d}\right) f(t−td)⟶yzs(t−td)
T [ { 0 } , f ( t − t d ) ] = y z s ( t − t d ) T[\{0\},f(t - t_d)] = y_{zs}(t - t_d) T[{0},f(t−td)]=yzs(t−td)
以灯泡开关为例。昨天,你把开关一开,灯亮了;今天,开关一开,灯也亮了就是时不变,如果灯没亮,就是时变。
1.4.2.5.2 时不变的直观判断方法
若 f ( ⋅ ) f (·) f(⋅)前出现变系数,或有反转、展缩变换,则该系统为时变系统。


1.4.2.5.3 LTI连续系统的微分特性和积分特性
线性时不变(Linear Time-Invariant)系统,简称LTI系统。
(1)微分特性:
若 f ( t ) → y z s ( t ) , 则 f ′ ( t ) → y z s ′ ( t ) 若 f (t) → y_{zs} (t), 则 f ' (t) → y_{zs}' (t) 若f(t)→yzs(t),则f′(t)→yzs′(t)
(2)积分特性:
若 f ( t ) → y z s ( t ) , 则 ∫ − ∞ t f ( x ) d x = ∫ − ∞ t y z s ( x ) d x 若 f (t) → y_{zs} (t), 则\int_{-\infty}^tf(x)dx=\int_{-\infty}^ty_{zs}(x)dx 若f(t)→yzs(t),则∫−∞tf(x)dx=∫−∞tyzs(x)dx
1.4.2.6 因果与非因果系统
定义
因果系统是指零状态响应不会出现在激励之前的系统。
即对因果系统,当 t < t 0 t\lt t_0 t<t0, f ( t ) = 0 f(t)=0 f(t)=0时,有 t < t 0 t\lt t_0 t<t0, y z s ( t ) = 0 y_{zs}(t)=0 yzs(t)=0
如下列系统均为因果系统:
y z s ( t ) = 3 f ( t − 1 ) y z s ( t ) = ∫ − ∞ t f ( x ) d x y_{\mathrm{zs}}(t)=3 f(t-1) \quad y_{z s}(t)=\int_{-\infty}^{t} f(x) d x yzs(t)=3f(t−1)yzs(t)=∫−∞tf(x)dx
而下列系统为非因果系统(还没开开关,仪器就开始工作):
( 1 ) y z s ( t ) = 2 f ( t + 1 ) 令 t = 1 时, 有 y z s ( 1 ) = 2 f ( 2 ) (1)y_{\mathrm{zs}}(t)=2 f(t+1) \text { 令 } t=1 \text { 时, } \text { 有 } y_{\mathrm{zs}}(1)=2 f(2) (1)yzs(t)=2f(t+1) 令 t=1 时, 有 yzs(1)=2f(2)
( 2 ) y Z s ( t ) = f ( 2 t ) 令 t = 1 时 , 有 y z s ( 1 ) = f ( 2 ) (2)y_{\mathrm{Zs}}(t)=f(2 t) \quad \text { 令 } t=1 \text { 时 }, \text { 有 } y_{\mathrm{zs}}(1)=f(2) (2)yZs(t)=f(2t) 令 t=1 时 , 有 yzs(1)=f(2)



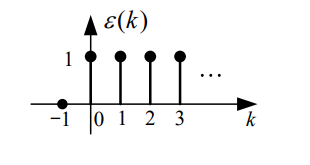
ε ( t ) 表 示 : t > 0 \varepsilon(t)表示:t>0 ε(t)表示:t>0
ε ( t − 1 ) 表 示 : t > 1 \varepsilon(t-1)表示:t>1 ε(t−1)表示:t>1
1.4.2.7 稳定系统与不稳定系统
一个系统,若对有界的激励 f ( ⋅ ) f(\cdot) f(⋅)所产生的零状态响应 y z s ( ⋅ ) y_{zs}(\cdot) yzs(⋅)也是有界的,则称该系统为有界输入有界输出稳定,简称稳定。即若 ∣ f ( ⋅ ) ∣ < ∞ |f(\cdot)|\lt \infty ∣f(⋅)∣<∞,其 ∣ y z s ( ⋅ ) ∣ < ∞ |y_{zs}(\cdot)|\lt \infty ∣yzs(⋅)∣<∞,则称该系统是稳定的。
《工程信号与系统》作者:郭宝龙等
国家精品课程:信号与系统 ,中国大学MOOC,郭宝龙,朱娟娟