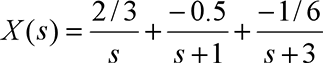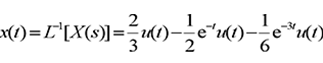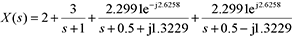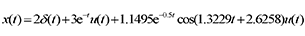---

1.基本信号的MATLAB表示

1.1.指数信号

%指数信号A*exp(a*t)
t = 0:0.1:10;
A = 1;
a = -0.4;
ft = A * exp(a *t );
plot(t,ft)

1.2.指数序列

%指数序列b^k使用.^实现
k = 1:0.1:10;
b = 3;
ft1 =  b.^k;
plot(ft1)

1.3.正弦型信号

注意信号是弧度制（sin）或角度值（sind）

%正弦信号sin,sind
m = 0:0.01:2*pi;
n = 0:1:360;
ft2 = sin(m);
ft3 = sind(n);
figure(3)
subplot(2,1,1)
plot(ft2)
title('弧度制')
subplot(2,1,2)
plot(ft3)
title('角度制')

1.4.抽样函数Sa(t)

Sinc(t)

clear all
clc
t = -10:0.01:10;
y = sinc(t);
plot(t,y);
xlabel('时间/s');ylabel('振幅'); title('抽样函数')

1.5.矩形脉冲函数

rectpuls(t,width)

产生一个幅值为1，宽度为2，相对于t=0点左右对称的矩形波信号，该函数的横坐标范围由向量t决定，是以t=0为中心向左右各展开width/2的范围，width的默认值为1
ylim([yl yr]);：限定y轴上限值，yl：下限，yr：上限
axis( [xmin xmax ymin ymax] )：设置当前坐标轴 x轴 和 y轴的限制范围

%矩形脉冲
width=2;
t=-2:0.001:3;
ft=rectpuls(t,width);
plot(t,ft)
%ylim([-1 2]) 
axis([-2,2,-1,2])

1.6.三角波脉冲信号

y=tripuls(T, w, s)

T是一个数组,表示信号时间
w是三角波的宽度（默认值为1）
s是三角波是斜率(-1<s<1)

%三角波脉冲
t=-3:0.001:3;
ft1=tripuls(t,4,0);
ft2=tripuls(t,4,1);
subplot(2,1,1)
plot(t,ft1)
subplot(2,1,2)
plot(t,ft2)

1.7.单位采样序列

直接生成：

%单位采样序列
k=-50:50;
delta=[zeros(1,50),1,zeros(1,50)];
stem(k,delta)

函数生成：

function [f,k]=unitimpuls(k0,k1,k2)
%产生 f[k]=delta(k-k0)；
%k1<=k<=k2
k=k1:k2;
f=(k-k0)==0;
end

k0 =0;k1=-50;k2=50;
[f,k]=unitimpuls(k0,k1,k2);
stem(k,f)

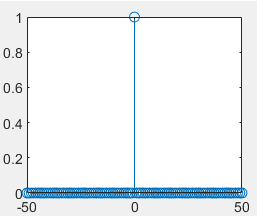
1.8.单位阶跃序列

直接生成：

%单位阶跃序列
k=-50:50;
uk=[zeros(1,50), ones(1,51)];
stem(k,uk)

函数生成：

function [f,k] = unitstep(k0,k1,k2) 
%产生 f[k]=u(k-k0);k1<=k<=k2
k=k1:k2;
f=(k-k0)>=0;
end

k0=0;k1=-50;k2=50;
[f,k]=unitstep(k0,k1,k2);
stem(k,f)

2.信号基本运算的MATLAB实现

2.1.信号的尺度变换、翻转、时移（平移）

压缩： 横坐标*n(n>1压缩，n<1扩展)
翻转： 横坐标*-1
平移： 横坐标+-n(左+右-)

%信号的尺度变换、翻转、时移（平移）
t=-4:0.001:4;
ft=tripuls(t,4,0.5); % 原始信号
subplot(2,2,1); plot(t,ft); title('x(t)')
ft1=tripuls(2*t,4,0.5); % 压缩
subplot(2,2,2); plot(t,ft1); title('x(2t)')
ft2=tripuls(-t,4,0.5); % 翻转
subplot(2,2,3); plot(t,ft2); title('x(-t)')
ft3=tripuls(t+1,4,0.5); % 平移
subplot(2,2,4); plot(t,ft3); title('x(t+1)')

2.2.信号的相加与相乘

相加： +
相乘： .*

%绘制信号波形
t=0:0.01:8;
A=1; a=-0.4;
w0=2*pi;phi=0;
ft1=A*exp(a*t).*sin(w0*t+phi);
plot(t,ft1)

2.3.离散序列的差分与求和

差分： y=diff(f);

y = [f(2)-f(1) f(3)-f(2) … f(m)-f(m-1)]

求和： y=sum(f(k1:k2))

y = f(k1)+f(k1+1)+…+f(k2)

2.4.连续信号的微分与积分

微分： y=diff(f)/h;

h为数值计算所取时间间隔

定积分： integral(function_handle,a,b);

function_handle被积函数句柄，a和b定积分区间

例子： 已知三角波x(t)，画出其微分与积分的波形

%已知三角波x(t)，画出其微分与积分的波形
% 原始信号
h=0.01;
t=-4:h:4;
ft=tripuls(t,4,0.5);
subplot(2,1,1);
plot(t,ft);
title('x(t)');
grid on
% 微分
y1=diff(ft)*1/h; 
subplot(2,2,3)
plot(t(1:length(t)-1),y1);
title('dx(t)/dt')
grid on
% 积分
for x=1:length(t) y2(x)=integral(@(t) tripuls(t,4,0.5),t(1),t(x));
end
subplot(2,2,4)
plot(t,y2)
title('\intx(t)dt')
grid on

3.利用MATLAB对LTI系统进行分析

线性时不变系统（LTI）： 参数不随时间改变，且满足叠加性和时不变性的系统

分析方法： 时域方法或变换域方法，如傅立叶变换、拉普拉斯变换和Z变换
系统分类： 连续时间系统和离散时间系统
描述方法： 常系数微分方程、系统的传递函数或状态方程

3.1.连续时间系统零状态响应的求解

y = lsim(sys,x,t)

t： 计算系统响应的抽样点向量
x： 系统输入信号向量
lsim： 针对线性时不变模型，给定任意输入，得到任意输出
sys： LTI系统模型

1. sys = tf(b,a)
2. b和a分别为微分方程右端（分子）和左端（分母）各项的系数向量

3.2.连续系统冲激响应和阶跃响应求解

冲激响应： y = impulse(sys,t)
阶跃响应： y = step(sys,t)

4.利用MATLAB对DTS系统进行分析

4.1.离散时间系统单位脉冲响应的求解

单位脉冲响应： h = impz(b,a,k)

sys： LTI系统模型
t： 计算系统响应的抽样点向量
k： 输出序列的取值范围
b, a： 分别是差分方程右、左端的系数向量

4.2.离散卷积的计算

离散卷积： c = conv(a,b)

a,b： 待卷积两序列的向量表示

conv函数也可用于计算两个多项式的积

5.3/4案例分析

1.零状态响应

求系统 y"(t)+2y’(t)+100y(t)=10x(t) 的零状态响应，已知x(t)=sin(2pt) u(t)

%连续时间系统零状态响应
ts=0;te=5;dt=0.01;
sys=tf([10],[1 2 100]);
t=ts:dt:te;
x=sin(2*pi*t);
y=lsim(sys,x,t);
plot(t,y);
xlabel('Time(sec)')
ylabel('y(t)')

ts=0;te=5;dt=0.01;
sys=tf([10],[1 2 100]);
t=ts:dt:te;
x=sin(2*pi*t);
lsim(sys,x,t);
grid on

2.冲激响应

求系统 y" (t)+2y ’ (t)+100y(t)=10x(t) 的冲激响应，已知x(t) =d (t)

%连续时间系统的冲激响应
ts=0;te=5;dt=0.01;
sys=tf([10],[1 2 100]);
t=ts:dt:te;
y=impulse(sys,t);
plot(t,y);
xlabel('Time(sec)')
ylabel('h(t)')

ts=0;te=5;dt=0.01;
sys=tf([10],[1 2 100]);
t=ts:dt:te;
impulse(sys,t)

3.滑动平均系统的响应

分析噪声干扰的信号x[k]=s[k]+d[k]通过M点滑动平均系统的响应

其中s[k]=(2k)0.9^k是原始信号，d[k]是噪声

%离散时间系统零状态响应
R =51 ; d = rand(1,R) - 0.5;
k=0:R-1;
s=2*k.*(0.9.^k); x=s+d;
figure(1); 
plot(k,d,'r-.',k,s,'b--',k,x,'g-');
M =5; b = ones(M,1)/M; a = 1;
%滤除向量x中的数据，向量b为x[k]、x[k-1]、…的系数，向量a为y[k]、y[k-1]、…的系数
y = filter(b,a,x);
figure(2); 
plot(k,s,'b--',k,y,'r-');

4.求单位脉冲响应

求系统y[k]+3y[k-1]+2y[k-2]=10x[k]的单位脉冲响应

% 离散系统的单位脉冲响应
k=0:10;
a=[1 3 2];
b=[10]; 
h=impz(b,a,k);
stem(k,h)

5.计算x[k]* y[k]并画出卷积结果

计算x[k]* y[k]并画出卷积结果，已知x[k]={1,2,3,4; k=0,1,2,3}，y[k]={1,1,1,1,1; k=0,1,2,3,4}

% 卷积
x=[1,2,3,4]; 
y=[1,1,1,1,1]; 
z=conv(x,y);
N=length(z);
stem(0:N-1,z);

6.利用MATLAB进行信号的频域分析

频谱Fn一般为复数，可分别利用abs和angle函数获得其幅频特性和相频特性
x = abs(Cn)
y = angle(Cn)

周期信号的频谱Cn为离散信号，可以用stem画出其频谱图

6.1.画出图示周期三角波信号的频谱

周期信号的频谱为：

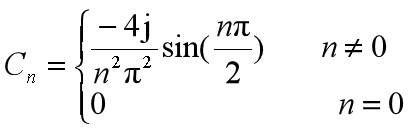
N=8;
%计算n=-N到-1的Fourier系数
n1= -N:-1; 
c1= -4*j*sin(n1*pi/2)/pi^2./n1.^2;
%计算n=0时的Fourier系数
c0=0;
%计算n=1到N的Fourier系数
n2=1:N; 
c2= -4*j*sin(n2*pi/2)/pi^2./n2.^2;
cn=[c1 c0 c2];
n= -N:N;
subplot(2,1,1);
stem(n,abs(cn));ylabel('Cn的幅度');
subplot(2,1,2);
stem(n,angle(cn));
ylabel('Cn的相位');
xlabel('\omega/\omega0');

6.2.用数值积分分析非周期信号频谱

y = integral(function_handle,a,b)

计算非周期信号频谱
function_handle： 函数句柄
a,b： 定积分的下限与上限

6.2.1.用数值方法近似计算三角波信号的频谱

三角波表示为：

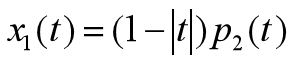
三角波信号频谱的理论值：X(jw)= Sa^2(w / 2)

sf = @(t,w)(t>=-1 & t<=1).*(1-abs(t)).*exp(-j*w*t);
% 三角脉冲信号傅里叶变换公式
w=linspace(-6*pi,6*pi,512);
N=length(w);X=zeros(1,N); 
% 数值积分计算频谱
for k=1:NX(k)=integral(@(t) sf(t,w(k)),-1,1);
end
subplot(2,1,1);
plot(w,real(X));title('')
xlabel('\omega');ylabel('X(j\omega)');
subplot(2,1,2);
plot(w,real(X)-sinc(w/2/pi).^2);
xlabel('\omega');title('计算误差');

7.利用MATLAB进行系统频域分析

7.1.连续系统频率响应的计算

H = freqs(b,a,w)

b： 分子多项式系数
a： 分母多项式系数
w： 需计算的H(jw)的抽样点(数组w中少需包含两个w的抽样点)
abs： 幅频特性
angle： 相频特性

例： 三阶归一化的Butterworth低通滤波器的系统函数为

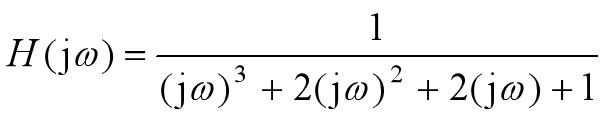
画出|H(jw)| 和φ(w)

w=linspace(0,5,200);
b=[1];a=[1 2 2 1];
h=freqs(b,a,w);
subplot(2,1,1);
plot(w,abs(h))
grid on
subplot(2,1,2);
plot(w,angle(h))
grid on

7.2.离散系统频率响应的计算

h = freqz(b,a,w)

b： 分子多项式系数
a： 分母多项式系数
w： 需计算的H(jw)的抽样点(数组w中少需包含两个w的抽样点)
abs： 幅频特性
angle： 相频特性

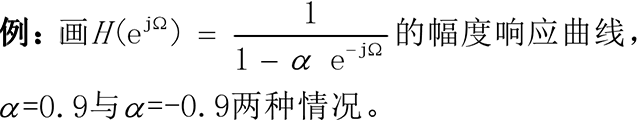
b = 1;
a1 = [1 -0.9];
a2 = [1 0.9];
w = linspace(0,2*pi,512);
h1 = freqz(b,a1,w);
h2 = freqz(b,a2,w);
plot(w/pi,abs(h1),w/pi,abs(h2),':')
legend('\alpha=0.9','\alpha=-0.9')

8.利用MATLAB进行连续系统的复频域分析

8.1.部分分式展开的MATLAB实现

[r,p,k] = residue(num,den)

num,den： 分别为X(s)分子多项式和分母多项式的系数向量
r： 部分分式的系数
p： 极点
k： 多项式系数（若为真分式，则k为零）

例： 用部分分式展开法求X(s)的反变换

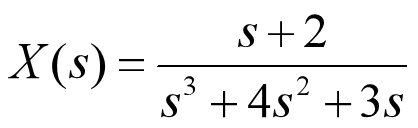
format rat %将结果数据以分数的形式输出
num=[1 2];
den=[1 4 3 0]; 
[r,p]=residue(num,den)

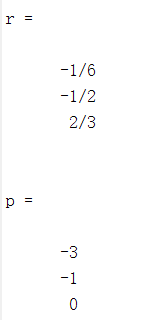
展开式：

反变换：

例： 用部分分式展开法求X(s)的反变换

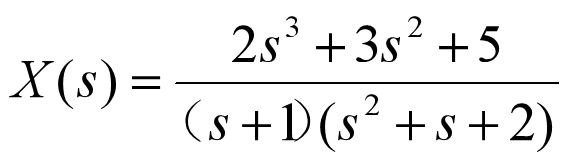
num=[2 3 0 5];
den=conv([1 1],[1 1 2]); 
%将因子相乘的形式转换成多项式的形式
[r,p,k]=residue(num,den)
magr=abs(r) %求r的模
angr=angle(r) %求r的相角

运行结果：
r =-2.0000 + 1.1339i, -2.0000 - 1.1339i, 3.0000
p =-0.5000 + 1.3229i, -0.5000 - 1.3229i, -1.0000
k =2
magr =2.2291, 2.2991, 3.0000
angr =2.6258, -2.6258, 0
展开式：

反变换：

8.2.H(s)的零极点与系统特性的MATLAB计算

r = roots(D)

计算多项式D(s)的根

[z,p,k] = tf2zp(b,a)

b、a： 分子多项式系数、分母多项式系数
z： 零点
p： 极点
k： 增益常数

pzmap(sys)

画出sys所描述系统的零极点图

例： 画出系统

的零极点分布图，求其单位冲激响应h(t)和频率响应H(jw)

num=[1];den=[1 2 2 1];
sys=tf(num,den); 
poles=roots(den)
figure(1);
pzmap(sys);
t=0:0.02:10;
h=impulse(sys,t);
figure(2);
plot(t,h)
title('Impulse Respone')
[H,w]=freqs(num,den);
figure(3);plot(w,abs(H))
xlabel('\omega')
title('Magnitude Respone')

num=[1];den=[1 2 2 1];
sys=tf(num,den); 
poles=roots(den)
figure(1);pzmap(sys);
figure(2)
impulse(sys);
figure(3)
freqs(num,den)

9.利用MATLAB进行离散系统的z域分析

9.1.部分分式展开的MATLAB实现

[r,p,k] = residuez(num,den)

num、den： 分子多项式和分母多项式的系数向量
r： 部分分式的系数
p： 极点
k： 多项式系数，若为真分式，则k为零

例： 将X(z)用部分分式展开

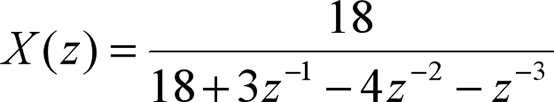
num = [18]; 
den = [18 3 -4 -1];
[r,p,k] = residuez(num,den)

运行结果
r =0.3600 , 0.2400 , 0.4000
p =0.5000 , -0.3333 , -0.3333
k =[]
展开式：

9.2.H(z)的零极点与系统特性的MATLAB计算

[z,p,k] = tf2zpk(b,a)

b、a： 分子多项式和分母多项式的系数向量
z： 零点
p： 极点
k： 增益常数

zplane(b,a)

绘制零极点分布图

例： 画出系统

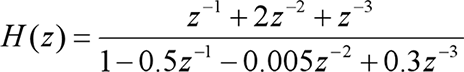
的零极点分布图，求其单位冲激响应h[k]和频率响应H(e^jΩ)

b =[0 1 2 1];a =[1 -0.5 -0.005 0.3];
figure(1);
zplane(b,a);
num=[0 1 2 1];
den=[1 -0.5 -0.005 0.3];
h=impz(num,den);
figure(2);
stem(h)
xlabel('k')
title('Impulse Respone')
[H,w]=freqz(num,den);
figure(3);
plot(w/pi,abs(H))
xlabel('Frequency \omega')
title('Magnitude Respone')

b =[0 1 2 1];a =[1 -0.5 -0.005 0.3];
figure(1);
zplane(b,a);
num=[0 1 2 1];
den=[1 -0.5 -0.005 0.3];
figure(2);
impz(num,den);
figure(3);
freqz(num,den);

例： 求出系统

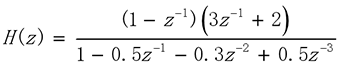
的零极点的值，单位冲激响应和频率响应

b=conv([1,-1],[2,3]); a=[1 -0.5 -0.3 0.5]; 
[z,p1,k1]=tf2zpk(b,a) 
figure(1)
zplane(b,a); 
figure(2)
impz(b,a); 
figure(3)
freqz(b,a) 

---