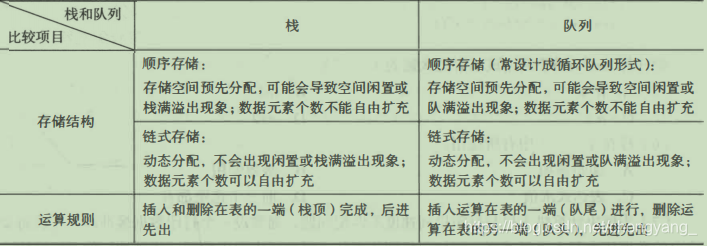
在学习通信原理之前，我们先回顾一下通信原理的数学理论基础——信号与系统讲了些什么，有哪些难以理解的问题。

下面开始第一章（以吴大正主编的第五版教材为依据，以下简称《信号》）

PS:这是我复习知识时整理的，习惯用费曼学习法讲一遍，大家凑合看吧，不喜欢随时×掉就行。另外因为是单纯地把知识过一遍，所以也不会放例题。

---

和所有的课程一样，第一章首先会介绍一些基本概念。在《信号》中，第一章介绍了信号与系统的概述。什么叫做信号、什么叫做系统、信号的分类、信号的基本运算以及两种基本信号。

首先我们拆解一下这个课程的名称：信号与系统。

第一个关键词是信号，我们在字典中查询一下：一种可以觉察的物理量或脉冲(如电压、电流、磁场强度等)，通过它们能传达消息或信息。那么这时候我们又需要区别“信息”与“信号”这两个东西。从这个意思里我们可以知道信号是信息传递的一个载体，这个载体可以是动作、光、声音、电波等等。 信号传递的信息可以是有用的，也可以是无用的，传递有用信息的信号称为有用信号，传递无用信息的信号称为噪声信号。

第二个关键词“系统”，指若干相互关联的事物组合而成具有特定功能的整体，信号系统的特定功能呢就是传输和处理信号了。输入的信号称为激励，输出的信号称为响应。在之后的通信原理中我们会专门学到通信系统，深入了解现代通信的奥秘。

所以信号与系统这门课程，就是一门研究信号经过系统产生变化的课程，在弱电课程系统中是以电路分析基础为基础的一门学科。电路不太懂也没关系，用到的时候自然懂了。

了解了什么是信号与系统，现在就让我们专注于信息载体——“信号"上面。人很喜欢做一件事情——贴标签，这是我们了解世界一种很实用的方式，接下来我们继续了解一些一些标签，以便在以后的学习工作中可以迅速地识别和分析。

• 确定信号

所谓”确定“就是可以根据信号之前的状态推测断定以后的状态。所以确定信号都可以用确定的函数来表示。确定信号里面呢又有几个比较重要的信号：指数信号、正弦信号、复指数信号、抽样信号，后面会说到。

• 随机信号

与确定信号相对的就是随机信号，它是随机的，不可预测的，很多干扰信号都是随机信号。比如这样的。

• 连续信号

一般来说，对于在时间上不间断的信号我们都称为连续信号，无论纵轴上是否连续。这种信号我们也可以称为模拟信号。

• 离散信号

同样，与连续信号相对的就是离散信号。离散信号又可以分为抽样信号（即在纵轴上连续的信号，这里要注意与Sa函数的区别）和数字信号（即在纵轴上不连续的信号）。

• 周期与非周期信号

这个概念呢比较简单，参考周期函数与非周期函数的定义，就不再赘述了。

• 能量信号

这个概念以前没有接触过，首先我们看一下在信号中对于能量和功率的定义。

将信号f(t)施加于1Ω电阻上，它所消耗的瞬时功率为|f(t) |^2，在区间(–∞ , ∞)的能量和平均功率定义为

根据定义知道能量是功率求和，功率是能量与时间的比值，注意这里是建立在无穷大时间积分的基础上的。

而能量信号全称是能量有限信号，这样说一下子就好理解了。在定义域内能量小于∞的信号就可以称为能量信号，那么有界限的值➗∞（也就是它的功率）就是一个0。一般来说，时限信号（只在有限时间内有值的信号）都是能量信号。

• 功率信号

类比，功率有限信号，定义域内功率＞0并且要小于∞。为什么要求功率要≠0呢？上面我们看见能量信号的功率是等于0的，为了避免定义之间的重叠，要求功率不能等于零，也就是说一个有限的值在无穷的时间里积分，得到的结果（也就是能量）就是∞。

由能量信号和功率信号的定义，得知能量信号和功率信号是相排斥的。一个信号不可能既是能量信号又是功率信号，但是可以既不是能量信号又不是功率信号。

• 一维信号和多维信号

自变量的个数称为维数。

• 因果信号与反因果信号

在t=0时，我们接入输入信号（也就是激励），那么按道理来说t=0之前是没有输出的，f(t)应该等于0，这时候我们就称f(t)为因果信号。一般来说，自然界中都是因果信号。如果t＜0的时候就有输出了呢？那它就被称为反因果信号。

• 指数信号、正弦信号

参考指数函数和正弦函数，这里不过赘述了。

• 复指数信号

根据欧拉公式，任何一个正弦信号都可以表示为复指数的形式，当然这个时候自变量不再是时间了。之后我们会详细说到。

• 抽样信号（辛格信号）

这是一个非常重要的信号，在接下来的学习中有很多的应用，它也叫辛格信号，为了不与另一个抽样信号相混淆，之后都称它为Sa函数。

Sa函数的性质比较多，具体的证明太多太麻烦这里就不说了，记住就行了。

接下来这两种信号标签非常非常重要，我们重点说一下。

• 阶跃信号

第一次看到这个概念可能会很陌生，但其实这个名字是非常形象的，我们画一下就知道了。就像阶梯一样，一下子从0跳跃到了1，所以我们叫它阶跃函数。

我们也可以看出，阶跃函数的定义就是

和其他函数的左右移动一样

搞清楚了定义，接下来再了解一下阶跃函数的性质，这里还是直接拿出来，不做过多证明。

• 冲激函数

现在这里有一个函数，发现当n→0时，我们就能得到上面我们刚说过的阶跃函数。在取极限之前，先对它进行一个求导，得到一个像门一样的函数，之后再取极限，就得到了最后这个图形。这就是冲激函数。这样，在函数有突变点的时候，我们也能表示出函数的导数。

同时，我们定义冲激函数的积分为1。

接下来，继续了解它的性质，同样我们直接给出不做证明。

okk，这就把基本的信号了解得差不多了。小时候我们学习12345……是为了算数，同样我们学习基本的信号，也是为了进行信号的运算（没错，和数字一样，信号也可以进行运算，信号的本质也是一个个数字嘛）。

这里我们先学习一些基本的信号运算，更高级的运算在之后的章节会讲到。

• 相加相乘

这个比较简单，一说就明白，就是对应横轴上进行纵轴的相加相乘，很容易理解。

举个栗子，左边是信号相加，右边是相乘。

• 积分微分

这个也很好理解，就是函数的积分和微分。当然在信号里会遇到很多阶跃函数微分成冲激函数、冲激函数积分成阶跃函数的时候。

• 时间变换

在时间这个横轴维度上分析信号时，经常会进行信号的时间变换，这也是非常重要的一个运算。包含平移、展缩、反转以及综合运算等。实际上在高中学习函数时应当学过函数的平移和展缩，所以接下来只简单说明一下反转。

将f(t) →f(–t) 称为对信号f(t)的反转或反折。 从图形上看是将f(t)以纵坐标为轴反转180°。

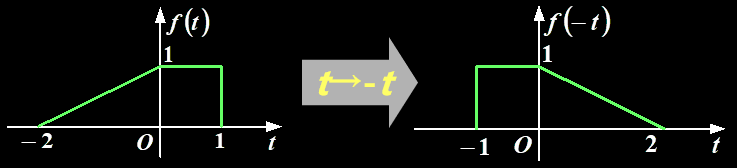
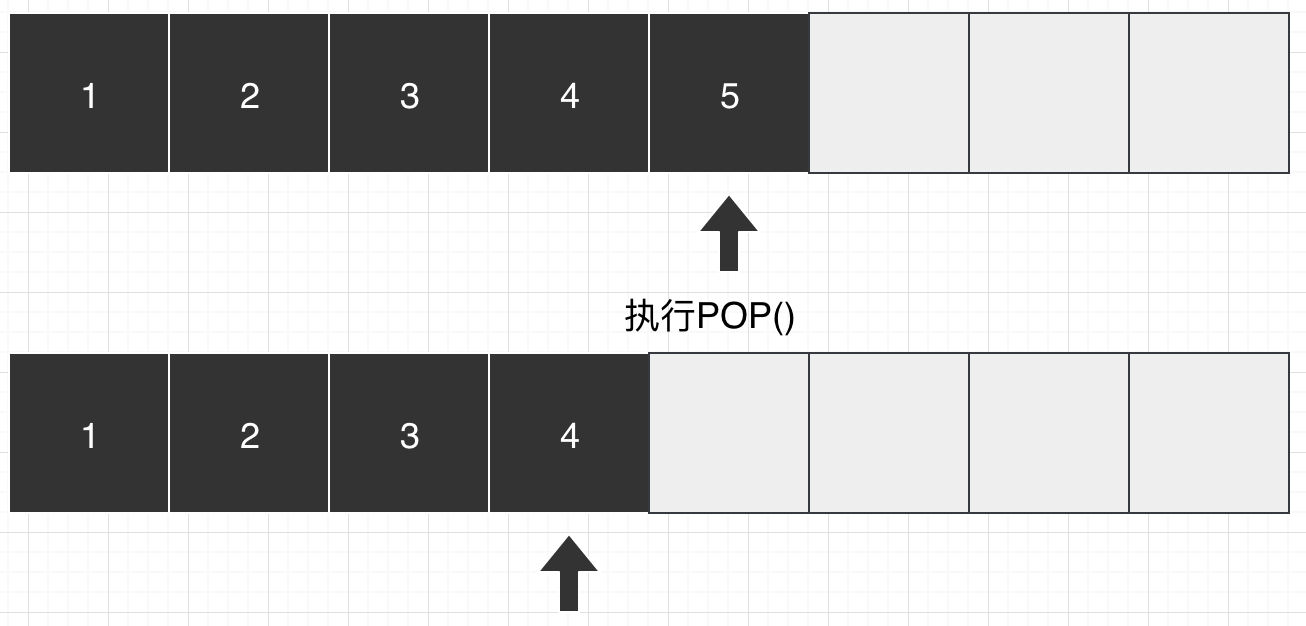
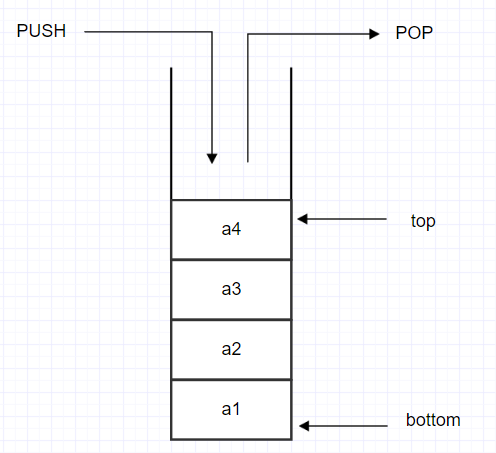
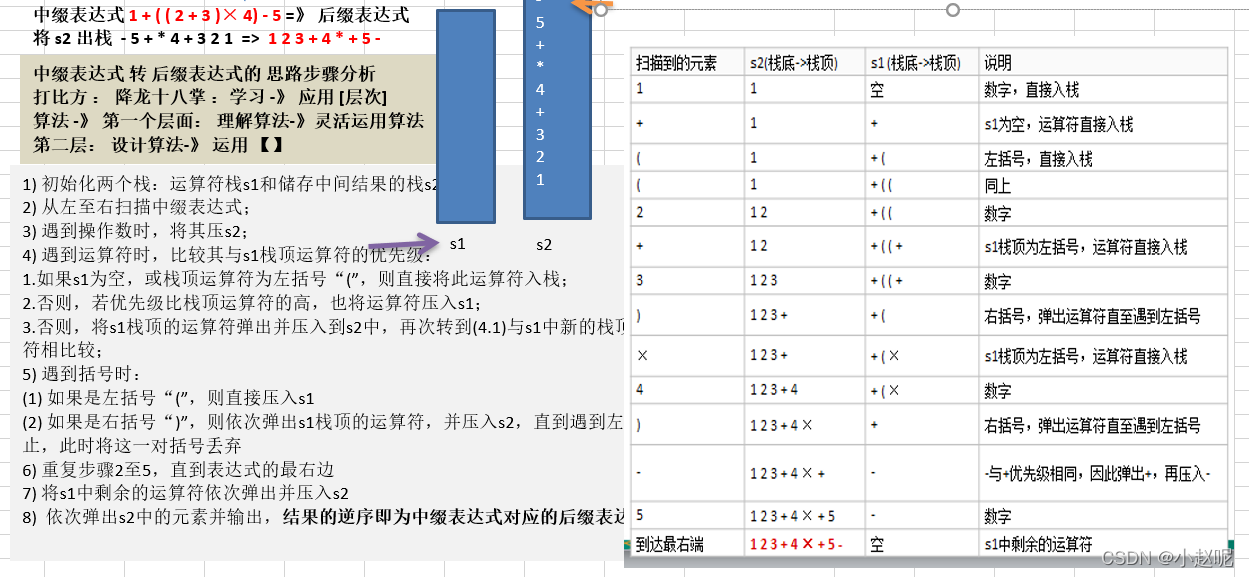
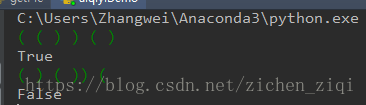
在实际中其实没有能够进行反转的器件，但是把信号数字化后我们可以做堆栈操作（先进后出，后进先出）来实现信号的反转。

❗要注意的是不管是平移、展缩还是反转，都是针对于 t 这个变量进行的。了解这一点后就不那么容易出错了。

愿每次回忆，对生活都不感到负疚。   ——郭小川

说完了“信号”，再来说一说“系统”，便于我们形成一个完整的体系。

刚开始我们就知道了系统是具有特定功能的总体，可以看作信号的变换器、处理器。接下来重复贴标签的操作，我们依然先了解一些标签。

• 连续系统与离散系统

这两个概念是基于时间域来说的。激励与响应都是连续信号的系统就叫连续系统，相对的激励与响应都是离散信号的系统就叫离散系统。如果激励与响应一个是连续的，一个是离散的，就叫混合系统。

• 动态系统与即时系统

若系统在任一时刻的响应不仅与该时刻的激励有关，而且与它过去的历史状况有关，则称为动态系统或记忆系统。含有记忆元件(电容、电感等)的系统是动态系统。否则称即时系统或无记忆系统。我们在下一章会重点说一下动态系统。

• 线性系统与非线性系统

这个性质以及接下来几个性质非常重要。所谓线性系统，就是满足线性性质（齐次性、可加性）的系统；不满足线性性质的系统自然被称为非线性系统。

线性性质：af1(·) +bf2(·)→ay1(·)+by2(·)

• 时不变系统与时变系统

在理解这个概念之前，首先需要知道什么是时不变性质。

所谓时不变性，也叫做移位不变性，激励在横轴上平移一段距离，那么响应也会在横轴相同方向上平移相同距离并且形状不变。就像下面这张图一样。

而拥有时不变性质的系统就叫做时不变系统，反之则叫时变系统。

之后的学习中经常会要求判断是否为线性时不变系统，用定义去判断就好了。至于线性时不变系统的性质，会在之后的章节介绍。

• 因果系统与非因果系统

类比因果信号，因果系统的零状态响应总是出现在输入之后（所谓零状态响应就是只与输入有关的响应）。即对因果系统，

。    若t<t0时，f(t) = 0，则有t<t0，yzs(t) = 0。实际的物理可实现系统均为因果系统。如果信号的自变量不是时间而是其他量（比如位移、距离、亮度等）的话，因果性就显得不是很重要了。

• 稳定系统与不稳定系统

只考虑激励在系统中产生的响应，也就是零状态响应，如果激励恒<∞，响应也永远有界，那么就说这个系统具有稳定性，是稳定系统；否则就是不稳定系统。

这样就搞定了不同系统的分类标签，接下来是描述系统的方法。

• 数学模型——方程

之前我们说了，信号可以用函数来表示，在输入函数和输出函数之间建立若干个关系，我们就能得到一系列的方程式，这就是系统的数学模型，可以分为微分方程（连续系统）和差分方程（离散系统）。高数中我们就学习过微分方程和差分方程的相关知识，在信号的学习中我们就能用上了。

• 框图表示

框图是学习信号中非常重要的一个工具，当然还有之后我们会学到的流程图。首先了解一下基本的框图单元和完整的框图结构，有个初步印象。

至此，我们已经学了不少关于信号和系统的知识了。第一章都是很基础的内容，很简单很好理解，这是之后学习的简化版，之后的学习中会深入地学习。