信号的描述和分类
信号的描述
函数表示
信号通常是时间变量t的函数,所以对于某一类信号可以用时间函数来表示,如
c ( u ) = { 0 , t < 0 e − t τ , t ≥ 0 c(u)=\begin{cases} 0,t<0\\ e^{-\frac{t}{\tau}}, t\geq0\end{cases} c(u)={0,t<0e−τt,t≥0
图形表示

数据表示
信号的分类
1、确定信号和随机信号
确定信号(determinate signal) 是指可以用时间变量t来表示的信号,是可以预测的
随机信号(random signal)是不能用时间变量t来表示的信号,是不可预测的,但是能记录
2、连续时间信号和离散时间信号
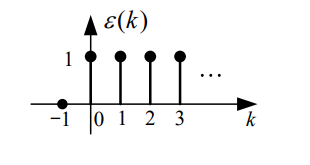
连续时间信号(continuous signal)是指时间变量取值t连续的信号,其图像为

离散信号(discrete-time signal)是值时间变量t取值不连续的信号,如图

周期信号与非周期信号
周期信号(periodic signal)是指在时间上重复某一变化规律的信号,如三角函数等
周期信号有三个特点
- 周期信号必须在时间上是无始无终的,即自变量t的取值范围t=R
- 随时间变化的规律必须具有周期性,其周期为T
- 在各周期内信号的波型完全一致
非周期信号是指不满足上面三个特点的信号
功率信号与能量信号
能量信号(energy signal)是指信号能量有限,而平均功率为0的信号
E = lim T → ∞ ∫ − T T ∣ f ( t ) ∣ 2 d t < ∞ E=\lim_{T\rightarrow\infty}{\int^{T}_{-T}{|f(t)|^2dt}}<\infty E=T→∞lim∫−TT∣f(t)∣2dt<∞
(例如非周期脉冲信号,只存在于有限时间的信号)
功率信号(power signal)是指信号平均功率有限,而信号能量无限大的信号
P = lim T → ∞ 1 T ∫ − T / 2 T / 2 ∣ f ( t ) ∣ 2 d t P=\lim_{T\rightarrow\infty}\frac{1}{T}\int^{T/2}_{-T/2}{|f(t)|}^2dt P=T→∞limT1∫−T/2T/2∣f(t)∣2dt
(例如,在时间间隔无限大的情况下,所有周期信号都是功率信号)
有时限信号和无时限信号
不言而喻
有始信号和有终信号
不言而喻
因果信号与非因果信号
t < 0 时 , f ( t ) = 0 , t ≥ 0 , f ( t ) ≠ 0 t<0时,f(t)=0,t \ge 0,f(t)\neq0 t<0时,f(t)=0,t≥0,f(t)=0,该信号为因果信号
t < 0 时 , f ( t ) ≠ 0 t<0时,f(t)\neq0 t<0时,f(t)=0,该信号为非因果