文章目录
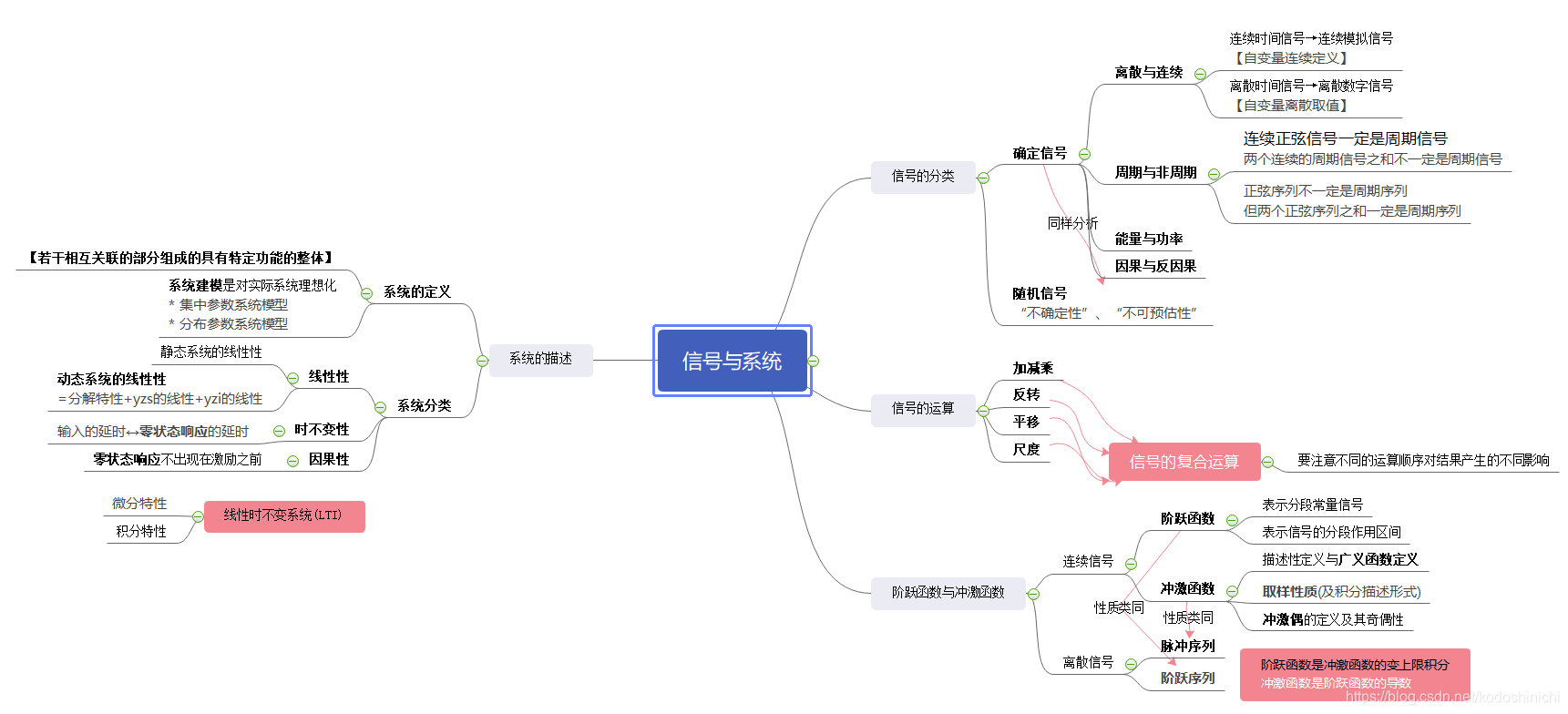
- 第一章 信号与系统概述
- 1.2基本信号
- 1.2.1 阶跃函数
- 1.2.2 冲激函数
- 1.2.3 冲激函数的广义函数定义
- 1.2.4 冲激函数的取样性质
- 1.2.5 冲激函数的导数
- 1.2.6 冲激函数的尺度变化
- 1.2.6.1 δ ( a t ) δ(at) δ(at) 的定义
- 1.2.6.2 推广结论
- 1.2.7 单位脉冲序列与单位阶跃序列
第一章 信号与系统概述
1.2基本信号
阶跃函数和冲激函数不同于普通函数,称为奇异函数。研究奇异函数的性质要用到广义函数(或分配函数)的理论。下面先直观引出阶跃函数和冲激函数。
1.2.1 阶跃函数
定义
选定一个函数序列 γ n ( t ) γ_n(t) γn(t) ,求极限。
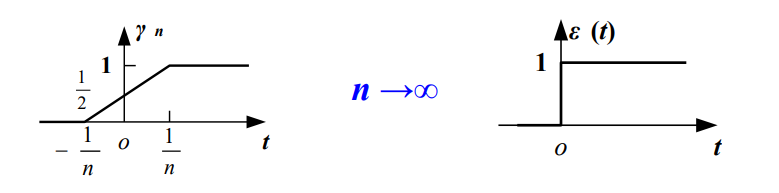
ε ( t ) = lim n → ∞ γ n ( t ) = { 0 , t < 0 1 / 2 , t = 0 1 , t > 0 \varepsilon(t)=\lim _{n \rightarrow \infty} \gamma_{n}(t)=\left\{\begin{array}{ll}0, & t<0\\1/2, &t=0 \\1, & t>0\end{array}\right. ε(t)=n→∞limγn(t)=⎩⎨⎧0,1/2,1,t<0t=0t>0
性质
(1)表示分段常量信号
f ( t ) = 2 ε ( t ) − 3 ε ( t − 1 ) + ε ( t − 2 ) f(t) = 2ε(t)- 3ε(t-1) +ε(t-2) f(t)=2ε(t)−3ε(t−1)+ε(t−2)

(2)表示信号的作用区间

(3)积分
∫ − ∞ t ε ( τ ) d τ = t ε ( t ) \int_{-\infty}^{t} \varepsilon(\tau) \mathrm{d} \tau=t \varepsilon(t) ∫−∞tε(τ)dτ=tε(t)
1.2.2 冲激函数
定义
单位冲激函数:是奇异函数,它是对强度极大,作用时间极短的物理量的理想化模型(狄拉克提出)。
{ δ ( t ) = 0 , t ≠ 0 ∫ − ∞ ∞ δ ( t ) d t = 1 \left\{\begin{array}{l}\delta(t)=0, \quad &t \neq 0 \\\\\int_{-\infty}^{\infty} \delta(t) d t=1\end{array}\right . ⎩⎨⎧δ(t)=0,∫−∞∞δ(t)dt=1t=0

理解: 高度无穷大,宽度无穷小,面积为1的对称窄脉冲。
冲激函数与阶跃函数的关系
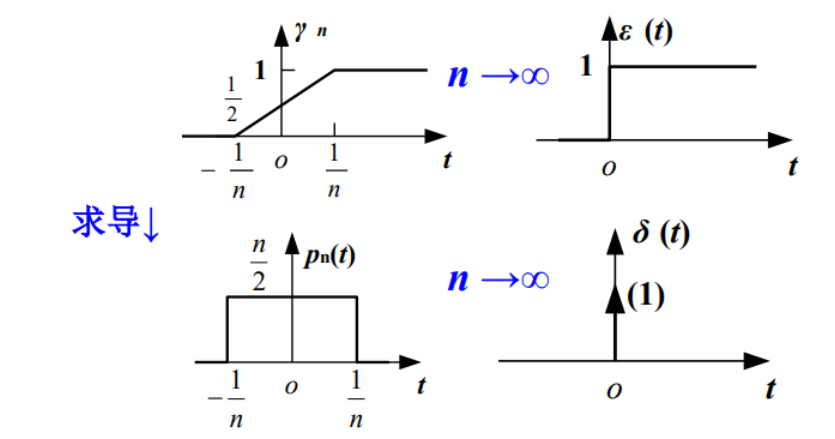
由
p n ( t ) = d γ n ( t ) d t p_n(t)=\frac{\mathrm{d} \gamma_n(t)}{\mathrm{d} t} \quad pn(t)=dtdγn(t)
得到:
δ ( t ) = d ε ( t ) d t \delta(t)=\frac{\mathrm{d} \varepsilon(t)}{\mathrm{d} t} \quad δ(t)=dtdε(t)
ε ( t ) = ∫ − ∞ t δ ( τ ) d τ \varepsilon(t)=\int_{-\infty}^{t} \delta(\tau) \mathrm{d} \tau ε(t)=∫−∞tδ(τ)dτ
作用:
冲激函数可以描述间断点的导数。

1.2.3 冲激函数的广义函数定义
广义函数定义
-
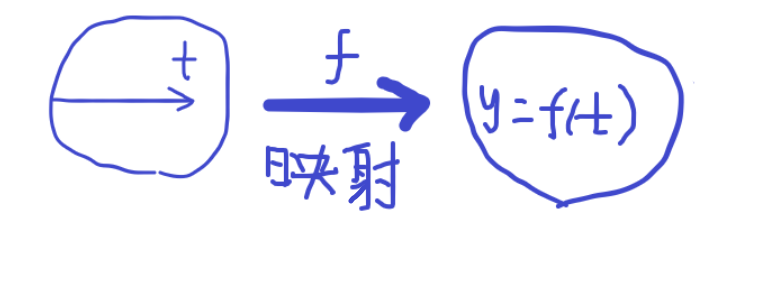
普通函数 y = f ( t ) y=f(t) y=f(t): 是将一维实数空间的数 t t t 经过 f f f所规定的运算映射为一维实数空间的数 y y y。
-
广义函数 N g [ φ ( t ) ] Ng[φ(t)] Ng[φ(t)]: 选择一类性能良好的函数 φ ( t ) φ(t) φ(t)作为检验函数(相当于自变量),一个广义函数 g ( t ) g(t) g(t)对检验函数空间中的
每个函数φ ( t ) φ(t) φ(t)赋予一个数值 N N N的映射记为:

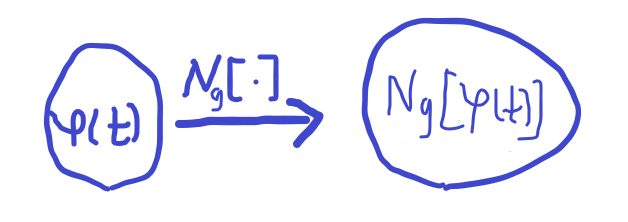
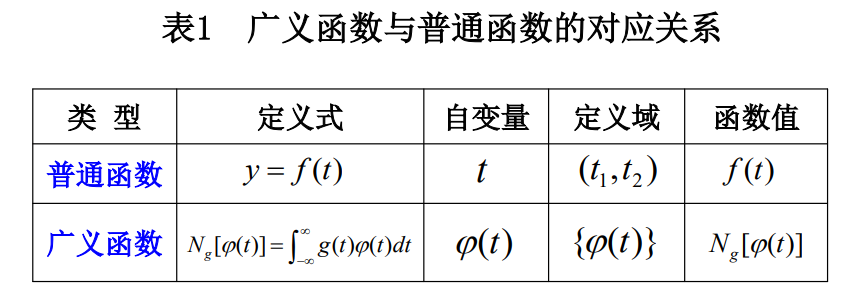
冲激函数的广义函数定义

含义: 冲激函数 δ ( t ) δ(t) δ(t)作用于检验函数 φ ( t ) φ(t) φ(t)的结果是赋值为 φ ( 0 ) φ(0) φ(0),称为冲激函数的取样性质 。
简言之,能从检验函数 φ ( t ) φ(t) φ(t)中筛选出函数值φ(0)的广义函数就称为冲激函数 δ ( t ) δ(t) δ(t) 。 举例如下:
高斯(钟形)函数
δ ( t ) = lim b → ∞ b e − π ( b t ) 2 \delta(t)=\lim _{b \rightarrow \infty} b e^{-\pi(b t)^{2}} δ(t)=b→∞limbe−π(bt)2
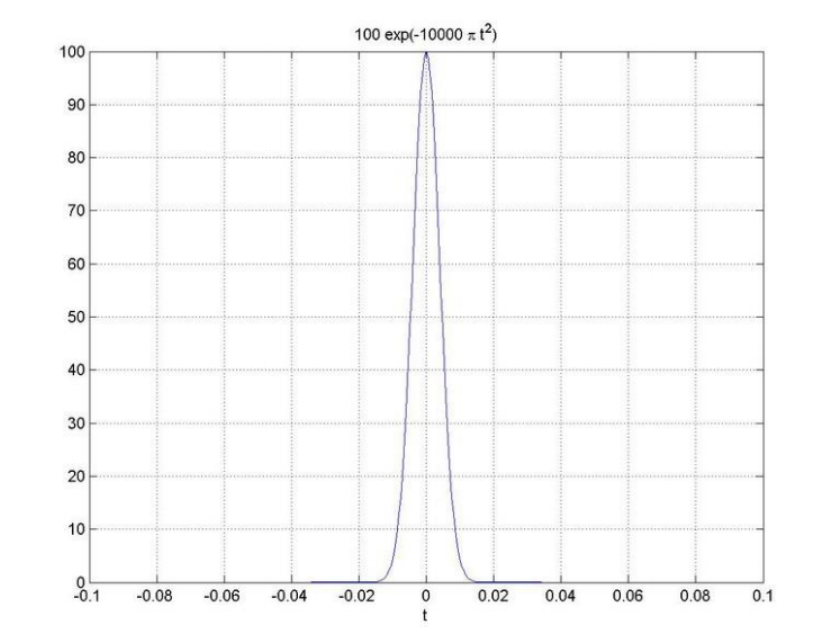
取样函数
δ ( t ) = lim b → ∞ sin ( b t ) π t \delta(t)=\lim _{b \rightarrow \infty} \frac{\sin (b t)}{\pi t} δ(t)=b→∞limπtsin(bt)
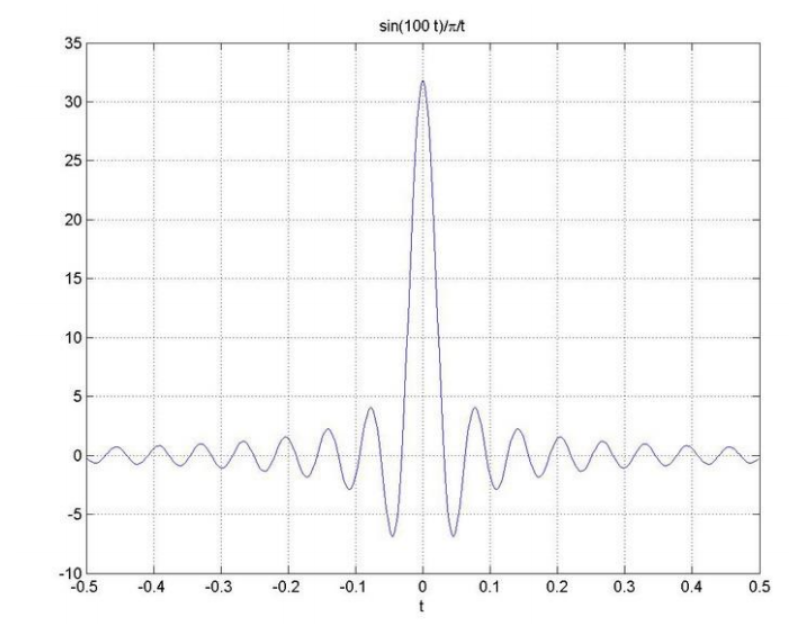
1.2.4 冲激函数的取样性质
1.2.4.1 f ( t ) f(t) f(t)乘以 δ ( t ) δ(t) δ(t)
f ( t ) δ ( t ) = f ( 0 ) δ ( t ) f(t) \delta(t)=f(0) \delta(t) f(t)δ(t)=f(0)δ(t)
f ( 0 ) δ ( t ) f(0)\delta(t) f(0)δ(t)含义 : : : f ( 0 ) f(0) f(0)倍的 δ ( t ) \delta(t) δ(t)
∫ − ∞ ∞ f ( t ) δ ( t ) d t = f ( 0 ) \int_{-\infty}^{\infty} f(t) \delta(t) \mathrm{d} t=f(0) ∫−∞∞f(t)δ(t)dt=f(0)
注意:积分区间要包含冲激所在的时刻 t = 0 t=0 t=0。
例子:
d d t [ e − 2 t ε ( t ) ] = e − 2 t δ ( t ) − 2 e − 2 t ε ( t ) = δ ( t ) − 2 e − 2 t ε ( t ) \frac{\mathrm{d}}{\mathrm{d} t}\left[\mathrm{e}^{-2 t} \varepsilon(t)\right]=\mathrm{e}^{-2 t} \delta(t)-2 \mathrm{e}^{-2 t} \varepsilon(t)=\delta(t)-2 \mathrm{e}^{-2 t} \varepsilon(t) dtd[e−2tε(t)]=e−2tδ(t)−2e−2tε(t)=δ(t)−2e−2tε(t)
∫ − 1 9 sin ( t − π 4 ) δ ( t ) d t = − 2 2 \int_{-1}^{9} \sin \left(t-\frac{\pi}{4}\right) \delta(t) \mathrm{d} t=-\frac{\sqrt{2}}{2} ∫−19sin(t−4π)δ(t)dt=−22
∫ − 4 − 1 sin ( t − π 4 ) δ ( t ) d t = 0 \int_{-4}^{-1} \sin \left(t-\frac{\pi}{4}\right) \delta(t) \mathrm{d} t= 0 ∫−4−1sin(t−4π)δ(t)dt=0
积分区间不包含0
1.2.4.2 f ( t ) f(t) f(t)乘以 δ ( t − a ) δ(t-a) δ(t−a)
f ( t ) δ ( t − a ) = f ( a ) δ ( t − a ) f(t) \delta(t-a)=f(a) \delta(t-a) f(t)δ(t−a)=f(a)δ(t−a)
∫ − ∞ ∞ f ( t ) δ ( t − a ) d t = f ( a ) \int_{-\infty}^{\infty} f(t) \delta(t-a) \mathrm{d} t=f(a) ∫−∞∞f(t)δ(t−a)dt=f(a)
注意:积分区间要包含冲激所在的时刻 t = a t =a t=a 。
例子:
∫ − 3 0 sin ( t − π 4 ) δ ( t − 1 ) d t = 0 \int_{-3}^{0} \sin \left(t-\frac{\pi}{4}\right) \delta(t-1) \mathrm{d} t= 0 ∫−30sin(t−4π)δ(t−1)dt=0
积分区间不包含1
∫ − 1 1 2 τ δ ( τ − t ) d τ = { 2 t , − 1 < t < 1 0 , 其它 \int_{-1}^{1} 2 \tau \delta(\tau-t) \mathrm{d} \tau=\left\{\begin{array}{lc}2 t, & -1<t<1 \\0, & \text { 其它 }\end{array}\right. ∫−112τδ(τ−t)dτ={2t,0,−1<t<1 其它
积分变量是 τ \tau τ,当 − 1 < t < 1 -1\lt t\lt 1 −1<t<1 时, δ ( τ − t ) \delta(\tau-t) δ(τ−t)才在 [ − 1 , 1 ] [-1,1] [−1,1]区间里。
∫ − 1 t ( τ − 1 ) 2 δ ( τ ) d τ = ε ( t ) \int_{-1}^{t}(\tau-1)^{2} \delta(\tau) \mathrm{d} \tau= \varepsilon(t) ∫−1t(τ−1)2δ(τ)dτ=ε(t)
当 t < 0 t<0 t<0时, δ ( τ ) \delta(\tau) δ(τ)积分等于0
1.2.5 冲激函数的导数
1.2.5.1 δ ’ ( t ) δ’(t) δ’(t) (也称冲激偶)
冲激函数的导数:瞬间冲上去,又冲下来。
f ( t ) δ ′ ( t ) = f ( 0 ) δ ′ ( t ) − f ′ ( 0 ) δ ( t ) f(t) \delta^{\prime}(t)=f(0) \delta^{\prime}(t)-f^{\prime}(0) \delta(t) f(t)δ′(t)=f(0)δ′(t)−f′(0)δ(t)
广义函数形式的定义:
∫ − ∞ ∞ δ ′ ( t ) f ( t ) d t = − f ′ ( 0 ) \int_{-\infty}^{\infty} \delta^{\prime}(t) f(t)\mathrm{d} t=-f^{\prime}(0) ∫−∞∞δ′(t)f(t)dt=−f′(0)
推广:
∫ − ∞ ∞ δ ′ ( t − a ) f ( t ) d t = − f ′ ( a ) \int_{-\infty}^{\infty}\delta^{\prime}(t-a) f(t) \mathrm{d} t=-f^{\prime}(a) ∫−∞∞δ′(t−a)f(t)dt=−f′(a)
例子:
∫ − ∞ ∞ ( t − 2 ) 2 δ ′ ( t ) d t = − d d t [ ( t − 2 ) 2 ] ∣ t = 0 = − 2 ( t − 2 ) ∣ t = 0 = 4 \int_{-\infty}^{\infty}(t-2)^{2} \delta^{\prime}(t) \mathrm{d} t=-\left.\frac{\mathrm{d}}{\mathrm{d} t}\left[(t-2)^{2}\right]\right|_{t=0}=-\left.2(t-2)\right|_{t=0}=4 ∫−∞∞(t−2)2δ′(t)dt=−dtd[(t−2)2]∣∣∣∣t=0=−2(t−2)∣t=0=4
∫ − ∞ ∞ ( t − 2 ) 2 δ ′ ( t − 1 ) d t = − d d t [ ( t − 2 ) 2 ] ∣ t = 1 = − 2 ( t − 2 ) ∣ t = 1 = 2 \int_{-\infty}^{\infty}(t-2)^{2} \delta^{\prime}(t-1) \mathrm{d} t=-\left.\frac{\mathrm{d}}{\mathrm{d} t}\left[(t-2)^{2}\right]\right|_{t=1}=-\left.2(t-2)\right|_{t=1}=2 ∫−∞∞(t−2)2δ′(t−1)dt=−dtd[(t−2)2]∣∣∣∣t=1=−2(t−2)∣t=1=2
1.2.5.2 δ ( n ) ( t ) δ^{(n)}(t) δ(n)(t)
∫ − ∞ ∞ f ( t ) δ ( n ) ( t ) d t = ( − 1 ) n f ( n ) ( 0 ) \int_{-\infty}^{\infty} f(t) \delta^{(n)}(t) \mathrm{d} t=(-1)^{n} f^{(n)}(0) ∫−∞∞f(t)δ(n)(t)dt=(−1)nf(n)(0)
1.2.6 冲激函数的尺度变化
1.2.6.1 δ ( a t ) δ(at) δ(at) 的定义
δ n ( a t ) = 1 ∣ a ∣ 1 a n δ n ( t ) \delta^{n}(a t)=\frac{1}{|a|} \frac{1}{a^{n}} \delta^{n}(t) δn(at)=∣a∣1an1δn(t)
特例:
δ ( a t ) = 1 ∣ a ∣ δ ( t ) \delta(a t)=\frac{1}{|a|} \delta(t) δ(at)=∣a∣1δ(t)
1.2.6.2 推广结论
(1) δ ( a t − t 0 ) = δ [ a ( t − t 0 a ) ] = 1 ∣ a ∣ δ ( t − t 0 a ) \delta\left(a t-t_{0}\right)=\delta\left[a\left(t-\frac{t_{0}}{a}\right)\right]=\frac{1}{|a|} \delta\left(t-\frac{t_{0}}{a}\right) δ(at−t0)=δ[a(t−at0)]=∣a∣1δ(t−at0)
(2)当 a = − 1 a=-1 a=−1时, δ ( n ) ( − t ) = ( − 1 ) n δ ( n ) ( t ) \delta^{(n)}(-t)=(-1)^{n} \delta^{(n)}(t) δ(n)(−t)=(−1)nδ(n)(t)
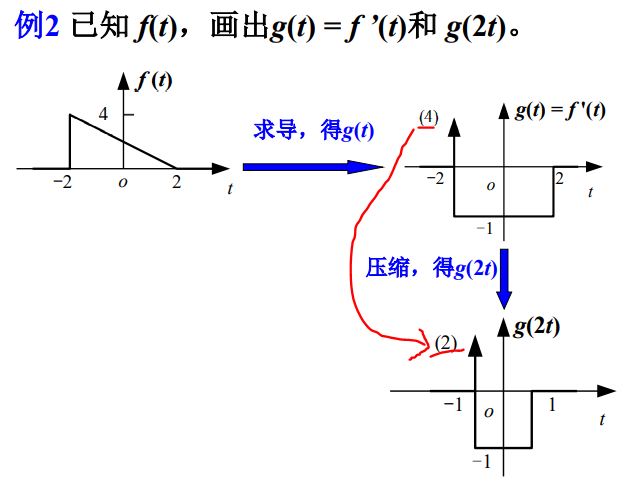
δ ( − t ) = δ ( t ) \delta(-t)=\delta(t) δ(−t)=δ(t), δ ( t ) \delta(t) δ(t)为偶函数。
δ ′ ( − t ) = δ ′ ( t ) \delta'(-t)=\delta'(t) δ′(−t)=δ′(t), δ ′ ( t ) \delta'(t) δ′(t)为奇函数。
 |  |
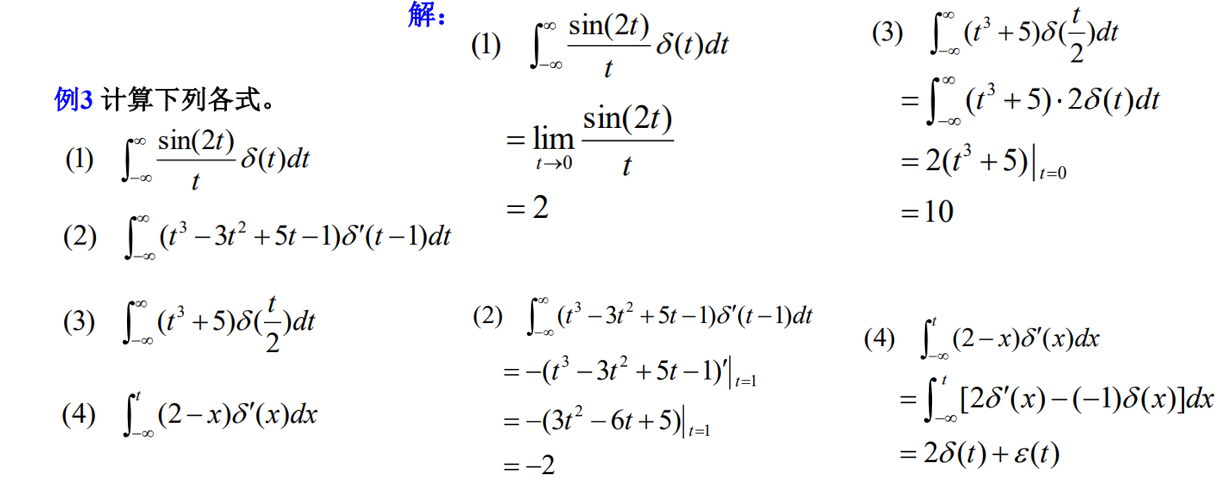
(3)由 ( t 3 + 5 ) ⋅ 2 δ ( t ) = ( 0 + 5 ) ⋅ 2 δ ( t ) (t^3+5)\cdot 2\delta(t)=(0+5)\cdot 2\delta(t) (t3+5)⋅2δ(t)=(0+5)⋅2δ(t)
得到 ∫ − ∞ ∞ ( 0 + 5 ) ⋅ 2 δ ( t ) d t = 10 \int_{-\infty}^{\infty}(0+5)\cdot 2\delta(t)dt=10 ∫−∞∞(0+5)⋅2δ(t)dt=10
(4)由 f ( t ) δ ′ ( t ) = f ( 0 ) δ ′ ( t ) − f ′ ( 0 ) δ ( t ) f(t) \delta^{\prime}(t)=f(0) \delta^{\prime}(t)-f^{\prime}(0) \delta(t) f(t)δ′(t)=f(0)δ′(t)−f′(0)δ(t)
得到 − x ⋅ δ ′ ( x ) = 0 ⋅ δ ′ ( x ) − 1 δ ( x ) -x\cdot\delta'(x)=0\cdot\delta'(x)-1\delta(x) −x⋅δ′(x)=0⋅δ′(x)−1δ(x)
1.2.7 单位脉冲序列与单位阶跃序列
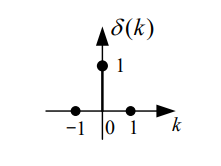
1.2.7.1 单位脉冲序列 δ ( k ) δ(k) δ(k)
对应冲激函数。
δ ( k ) = { 1 , k = 0 0 , k ≠ 0 \delta(k)=\left\{\begin{array}{ll}1, & k=0 \\0, & k \neq 0\end{array}\right. δ(k)={1,0,k=0k=0
取样性质:
f ( k ) δ ( k ) = f ( 0 ) δ ( k ) f(k) \delta(k)=f(0) \delta(k) f(k)δ(k)=f(0)δ(k)
f ( k ) δ ( k − k 0 ) = f ( k 0 ) δ ( k − k 0 ) f(k) \delta\left(k-k_{0}\right)=f\left(k_{0}\right) \delta\left(k-k_{0}\right) f(k)δ(k−k0)=f(k0)δ(k−k0)
∑ k = − ∞ ∞ f ( k ) δ ( k ) = f ( 0 ) \sum_{k=-\infty}^{\infty} f(k) \delta(k)=f(0) k=−∞∑∞f(k)δ(k)=f(0)
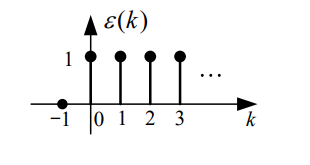
1.2.7.2 单位阶跃序列 ε ( k ) ε(k) ε(k)
ε ( k ) = { 1 k ≥ 0 0 , k < 0 \varepsilon(k)=\left\{\begin{array}{ll}1 & k \geq 0 \\0, & k<0\end{array}\right. ε(k)={10,k≥0k<0
1.2.7.3 ε ( k ) ε(k) ε(k)与 δ ( k ) δ(k) δ(k)的关系
δ ( k ) = ε ( k ) − ε ( k − 1 ) \delta(k)=\varepsilon(k)-\varepsilon(k-1) δ(k)=ε(k)−ε(k−1)
ε ( k ) = ∑ i = − ∞ k δ ( i ) \varepsilon(k)=\sum_{i=-\infty}^{k} \delta(i) ε(k)=i=−∞∑kδ(i)
或
ε ( k ) = ∑ j = 0 ∞ δ ( k − j ) = δ ( k ) + δ ( k − 1 ) + … \varepsilon(k)=\sum_{j=0}^{\infty} \delta(k-j)=\delta(k)+\delta(k-1)+\ldots ε(k)=j=0∑∞δ(k−j)=δ(k)+δ(k−1)+…
《工程信号与系统》作者:郭宝龙等
国家精品课程:信号与系统 ,中国大学MOOC,郭宝龙,朱娟娟