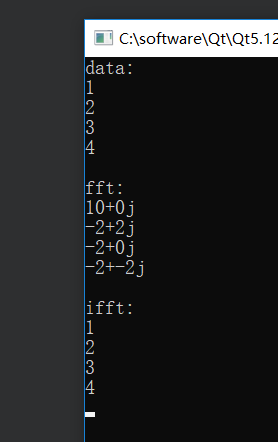
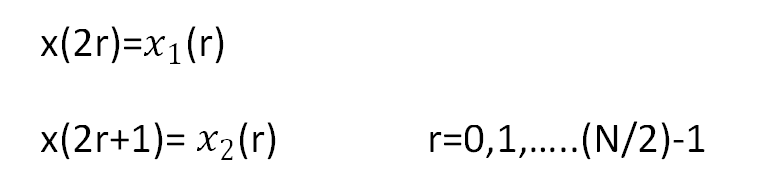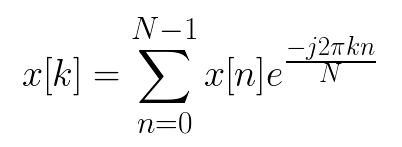FFT算法实现

厚

2.1实验目的

I、加深对快速傅里叶变换的理解。
II、掌握 FFT 算法及其程序的编写。
III、掌握算法性能评测的方法。
IV、熟悉MatLab编程。

2.2实验原理

一个连续信号Xa(t)的频谱可以用它的傅里叶变换表示为：

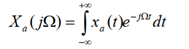
如果对该信号进行理想采样，可以得到采样序列：

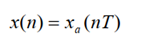
同样可以对该序列进行z变换，其中T为采样周期：

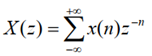
当z=e^jω的时候，我们就得到了序列的傅里叶变换：

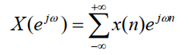
其中w称为数字频率，它和模拟域频域的关系为：

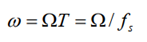
其中fs是采样频率。上式说明数字频率是模拟频率对采样率 fs 的归一化。同模拟域的情况相似，数字频率代表了序列值变化的速率，而序列的傅立叶变换称为序列的频谱。序列的傅立叶变换和对应的采样信号频谱具有下式的对应关系。

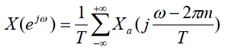
即序列的频谱是采样信号频谱的周期延拓。从上式可以看出，只要分析采样序列的频谱，就可以得到相应的连续信号的频谱。
在各种信号序列中，有限长序列在数字信号处理中占有很重要的地位。无限长的序列也往往可以用有限长序列来逼近。对于有限长的序列我们可以使用离散傅立叶（DFT），这一变换可以很好地反应序列的频域特性，并且容易利用快速算法在计算机上实现当序列的长度是 N 时，我们定义离散傅立叶变换为：

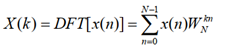
其中W_N=e^(-2Πj/N)，它的反变换定义为：

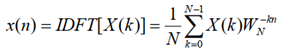
若直接计算DFT变换，整个DFT运算需要4N^2次实数相乘和2N(2N-1)次实数相加。
所以直接计算乘法次数与加法次数都和N^2成正比。例如N=10点的DFT，需要100次复数相乘，而N=1024时则需要1,048,576即一百多万次复数乘法运算。这对于实时性要求很强的信号处理来说，必将对计算速度有十分严苛的要求。为此，FFT作为对DFT的改进诞生。
快速傅里叶变换FFT并不是与DFT不相同的另一种变换，而是在DFT计算规律上建立的一种减少运算次数的快速算法。常用FFT是以基-2的，长度N=2^M。运算效率高，程序简单，使用方便。本实验就使用以2为基实现FFT。算法流程图可以用蝶形算法来表示，以8点的基2-FFT算法为例：

每个蝶形运算为：

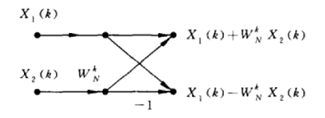
可以看到，每个蝶形运算都可原位运算。
当需要进行变换的序列长度不是2 的整数次方的时候，为了使用以 2 为基的 FFT，可以用末尾补零的方法，使其长度延长至 2 的整数次方。IFFT一般可以通过 FFT 程序来完成，只要对 X(k)取共轭，进行 FFT 运算，然后再取共轭，并乘以因子 1/N，就可以完成 IFFT。

2.3实验内容

1、算法实现
以对高斯序列进行FFT代码为例：

①、使用bitrevorder()函数对待变换信号顺序进行调整，存入x1中。例如M=8时
原顺序：000(0)，001(1)，010(2)，011(3)，100(4)，101(5)，110(6)，111(7)

对二进制翻转之后为：

新顺序：000(0)，100(4)，010(2)，110(6)，001(1)，101(5)，011(3)，111(7)

对比实验原理中M=8的FFT输入序列发现两者顺序一致。
②、n=1:m1表示一共有m1层运算，比如M=8时有3层。
k=1:M/(2^n)表示第n层分为k部分，比如M=8的第一层分为4个单独蝶形运算，第二层分为2个两两蝶形运算，第三部分为1个四四蝶形运算。
m表示第k部分的第m个蝶形运算。
③、因为蝶形运算是原位运算，就不需要另外开辟空间，计算结果仍然存在原位置。
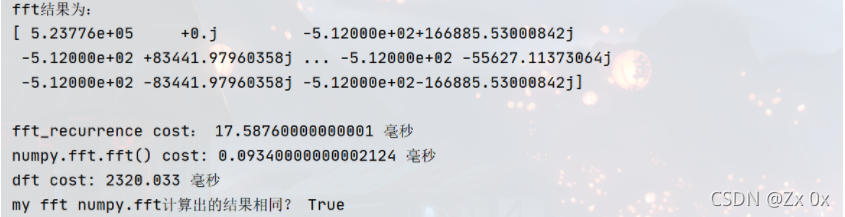
④、绘出编写的FFT计算结果与MATLAB的FFT计算结果，以及两者的差。
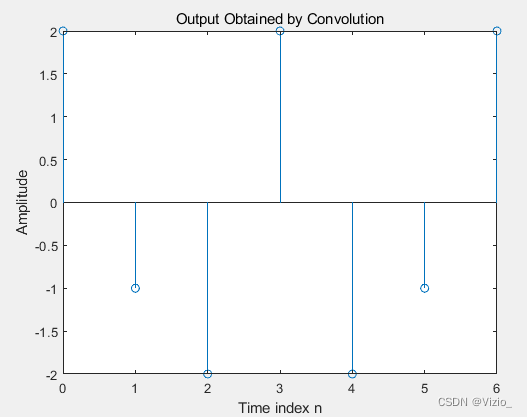
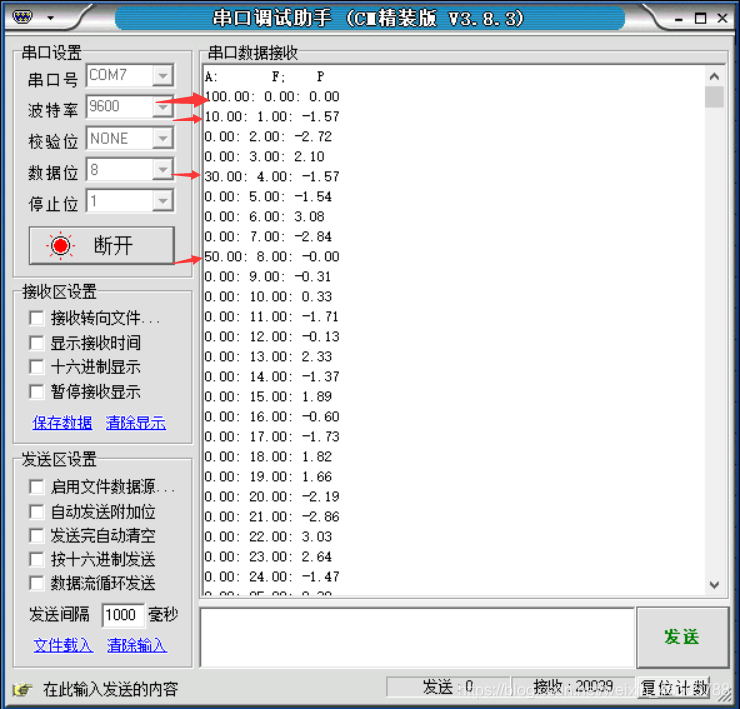
2、选取实验 1 中的典型信号序列验证算法的有效性
I、三角波

II、反三角波

III、高斯序列

IV、衰减正弦序列

V、单位脉冲序列

VI、矩形窗序列

VII、理想采样序列

注意每个序列自己编写的FFT计算结果和MATLAB的FFT计算结果，两者相差数量级
在10^(-16)到10(-14)。说明编写的FFT算法正确性没有问题。

3、对所编制的FFT算法进行性能评估
算法的评估首先是其正确性，是否能够完成预期功能决定了该算法是否有意义，
上一部分已经通过典型信号序列验证了编写的FFT算法的有效性。
这里接下来主要从时间复杂度和空间复杂度两方面来进行评价。空间复杂度是指该算法运行过程需要占用多少内存空间，随着半导体产业的发展，内存空间变得越来越廉价，空间复杂度对算法性能的影响也越来越小。人们往往根据时间复杂度来评价一个算法的性能。而时间复杂度主要依赖于算法的计算次数。已知基2-FFT算法的复数乘法次数为1/2 〖Nlog〗_2 N。相比于加法，乘法在运算中要复杂得多，占用资源也更多，所以时间复杂度主要依赖乘法次数。从理论复杂度来看，FFT显然比DFT的N^2更优。在MARLAB中查看程序运算时间有以下办法：

①、tic和toc命令组合
tic；
operation；
toc；
tic用来保存当前时间，也就是operation开始运行时间，toc用来记录程序完成时间。MATLAB会自动计算时间差并显示（以秒为单位但能精确到小数点后6位，即us）。

②、etime(t1,t2)和clock配合
t1=clock；
operation；
t2=clock；
etime(t1,t2);
通过调用windows系统时钟进行时间差计算得到运行时间，t1和t2之间的时间差。

③cputime函数
t1=cputime；
operation；
t2=cputime-t1；
使用cpu主频计算运行时间差，得到程序运行时间。

tic/toc是MATLAB自身计数器，精度要高于后两者。而且，如②调用系统时钟计算时间差，这段时间中系统可能还有其他后台程序。
MATLAB官方推荐使用tic/toc组合，When timing the duration of an event,use the tic and toc functions instead of clock or etime.所以接下来的评估程序运行时间，本实验使用tic/toc命令。此外，程序运行时间和计算机本身的计算能力有着直接关系，以下数据都是在个人笔记本电脑测得。由于电脑属于商务本，计算能力很有限，时间相对会稍长一些。
以上主要说明了FFT算法评估方法和侧重点，具体评估数据在下面的dofft与DFT、dofft与MATLAB-FFT的性能比较中给出。

2.4实验报告要求

1、总结自己实现的FFT算法时采用了哪些方法减少了运算量。
1）使用matlab的bitrevorder()函数实现二进制翻转，由于matlab的函数是基于更底层的的c语言编写的，有很专业的优化，执行速度肯定更快。
2）尽量使用小循环套大循环，因为执行的跳转原因，大循环单次执行时间优于小循环。
3）利用蝶形运算的原位性，使用同一个地址空间存储变换前序列和变换后序列。
4）每相邻计算的蝶形运算数据在地址上尽量连续，减少寻址时间。
2、给出自己的FFT算法与实验1中的DFT算法性能比较结果。
为避免运算时间过短不利于记录，使用20次循环。dofft程序见2.3，其余程序如下
DFT程序：

dofft测试程序：

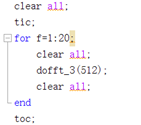
DFT测试程序：

运行时间记录如下：
N
算法 8 32 256 512 1024 2048
dofft 1.524102 1.563602 1.820989 1.984634 2.814433 3.088558
DFT 0.367555 0.375953 0.945036 4.491770 22.746014 107.771205
作图：

测试序列为理想采样序列。为避免循环运行时，MATLAB程序在前一循环已在内存中开辟空间和留有数据，测试程序中使用了clear all命令来清除内存中的数据。这样测得的时间更加准确。从记录的运行时间中可以看到，当N比较小的时候，DFT运行时间比dofft时间更小，这是因为DFT算法使用的是向量运算，而dofft中使用了循环。MATLAB本身对于向量计算的速度快于循环的计算速度。所以如果进一步优化dofft算法，可以改用向量运算，避免循环。当N趋于更大时,DFT运行时间迅速上升，很快 和dofft运行时间不在一个数量级。这和DFT、FFT两算法的理论时间复杂度一致。
3、给出自己的FFT算法和MATLAB中fft算法性能比较结果。
采用与2中相同的测试方法，同样使用20次循环。

fft程序：

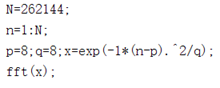
fft测试程序：

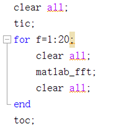
运行时间记录如下：
N
算法 512 1024 2048 4096 8192
dofft 1.984634 2.814433 3.088558 3.579388 5.438975
FFT 0.349001 0.369433 0.365632 0.403413 0.334651
N
算法 16384 32768 65536 131072 262144
dofft 13.307104 18.961649 28.585727 61.441558 125.271445
FFT 0.350225 0.431561 0.430717 0.445077 0.530932
作图：

自己编写的dofft在进行变换长度的横坐标下近似线性增长。而MATLAB本身的FFT基本上随着N的增大，运行时间基本上没有变化。显然dofft性能比fft性能差。想必MATLAB中的fft函数进行了更多技巧和优化。

4、总结实验中根据实验现象得到的其他结论。

①实验中测运行时间，当前后两个程序运行时间相差不大时，可能时间大小有波动。比如MATLAB中的fft函数在做2048点计算时所用时间比1024点计算时间稍小，这与MATLAB当前占CPU和电脑状态相关。也会出现同一个程序在不同时刻测运行时间大小稍有差异，多测几次时间取平均时间长。
②DFT在N较小时运行时间小于dofft，说明MATLAB更优于计算向量。所以编写MATLAB程序时应尽量把for循环改为矩阵运算，尽量向量化。
③同样的算法，基于不同的编程，在运行速度上仍然会有很大的不同，比如在MATLAB中使用for循环编写，MATLAB本身的FFT，和用C语言编写的FFT在运行速度上都会有很大不同。所以提高编程技巧，了解程序具体流水线、地址开辟、循环嵌套等等如何对优化程序有很大意义。
④MATLAB带有众多功能强大，高优化水平的函数，在编写程序时，尽可能查询MATLAB有无相关函数，充分利用，以提高编写的程序的执行效率，比如dofft中的bitreorder。
⑤测量运行时间的时候要把绘图的函数注释掉，否者会占用程序大量运行时间。