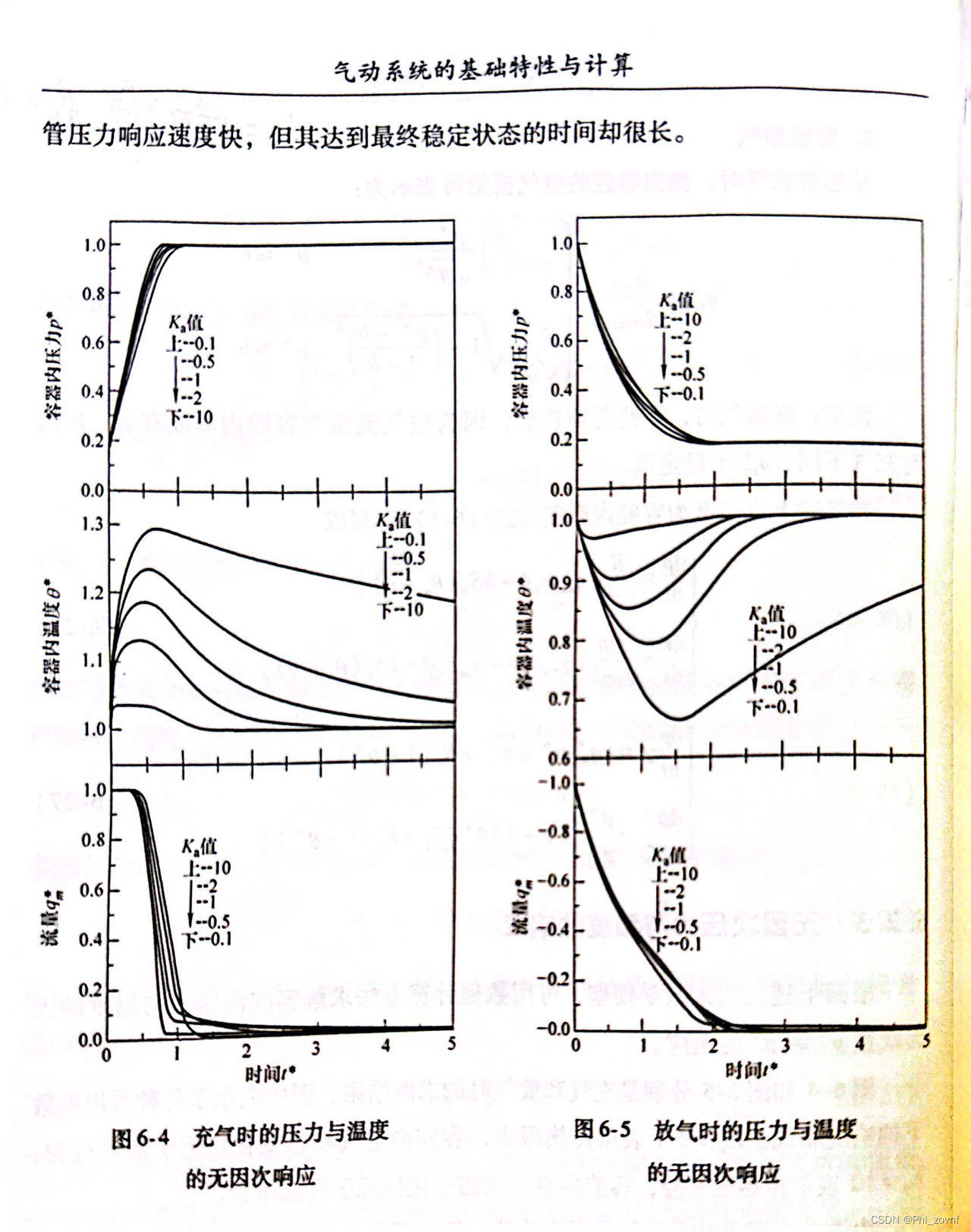
问题描述

两个n次多项式相乘，其时间复杂度为$O(n^2)$,通过FFT来减小其问题的复杂度。

分析过程

1. FFT的基本思路是：我知道一个多项式表达式可以根据其表达式算出结果，同理我们也可以根据其结果算出表达式。
2. 对于A，B两个n次多项式，一共所有又2n+1个参数需要求解，我们至少需要2n+1个表达式。
   FFT基本步骤：
3. 选择：选择至少2n+1个点。
4. 计算：分别计算出$A(x_0),A(x_1),......,A(x_{2n+1})$和$B(x_0),B(x_1),......,B(x_{2n+1})$,再通过$C(x_k) = A(x_k)B(x_k)$算出对应的C值。
5. 通过这些多项式等式求解C相应的系数。
   通过对上面的分析:可以发现第4步的时间复杂度为$O(n^2)$，所以得想办法减少其时间复杂度。所以我们对第4步的计算采取分而治之的策略。如下图所示：
   
   原本需要两个$O(n)$的时间复杂度，现在一个就可以了。我们要如何构造x值，使得计算复杂度变为$nlogn$。

数学准备

1. 一个复数可以表示成$z = a + bi$（这是笛卡尔的坐标表示），变形可以得到 z