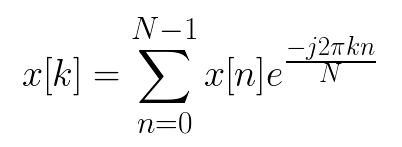关注、星标公众号，精彩内容每日送达

来源：网络素材

　随着数字技术的快速发展，数字信号处理已深入到各个学科领域。在数字信号处理中，许多算法如相关、滤波、谱估计、卷积等都可通过转化为离散傅立叶变换(DFT)实现，从而为离散信号分析从理论上提供了变换工具。但DFT计算量大，实现困难。快速傅立叶(FFT)的提出，大大减少了计算量，从根本上改变了傅立叶变换的地位，成为数字信号处理中的技术之一，广泛应用于雷达、观测、跟踪、高速图像处理、保密无线通信和数字通信等领域。
　　目前，硬件实现FFT算法的方案主要有：通用数字信号处理器(DSP)、FFT专用器件和现场可编程门阵列(FPGA)。DSP具有纯软件实现的灵活性，适用于流程复杂的算法，如通信系统中信道的编译码、QAM映射等算法。DSP完成FFT运算需占用大量DSP的运算时间，使整个系统的数据吞吐率降低，同时也无法发挥DSP软件实现的灵活性。采用FFT专用器件，速度虽能够达到要求。但其外围电路复杂，可扩展性差，成本昂贵。随着FPGA发展，其资源丰富，易于组织流水和并行结构，将FFT实时性要求与FPGA器件设计的灵活性相结合，实现并行算法与硬件结构的优化配置，不仅可以提高处理速度，并且具有灵活性高。开发费用低、开发周期短、升级简单的特点。针对某OFDM系统中FFT运算的实际需要，提出了基于FPGA的设计来实现FFT算法，并以16位长数据，64点FFT为例，在QuartusⅡ软件上通过综合和仿真。
　　2 FFT原理及算法结构
　　FFT是离散傅立叶变换(DFT)的快速算法。对于N点离散的有限长时问序列x(n)，其傅里叶变换为：
　

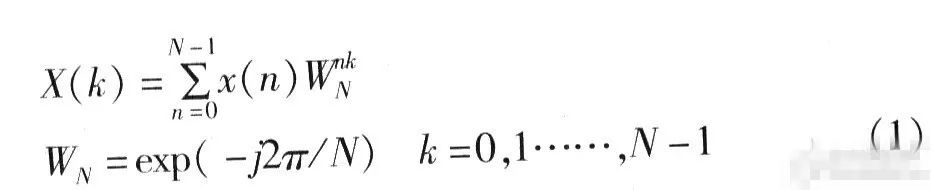
　　完成N点的DFT需要N2次复数乘法和N(N-1)次复数加法。点数大时，计算量也大，所以难以实现信号的实时处理。FFT的基本思想是利用旋转因子WN的周期性、对称性、特殊性以及周期N的可互换性，将长度为N点的序列DFT运算逐次分为较短序列的DFT运算，合并相同项，大大减少了计算量。
　　FFT算法分为两大类：一类是针对N=2的整数次幂的算法，如基2算法、基4算法、实因子算法和分裂算法等：另一类是N≠2的整数次幂算法，以winograd为代表的一类算法。硬件实现时，不仅要考虑算法运算量的大小，而且要考虑算法的复杂性和模块化。控制简单、实现规整的算法在硬件系统中要优于仅降低运算量的算法。现有FFT算法的FPGA设计方案基本上都是针对于类算法，而第二类算法尽管有其重要的理论价值，但硬件不易实现。由于该设计点数不是太多，综合考虑FFT处理器的面积和成本。所以采用按时间抽取的基2快速傅立叶算法(基2DIT-FFT)。
　　对于长度为N=2m的序列x(n)，其中m是整数，将x(n)按奇偶分成两组，即令：n=2r和n=2r+1，而r=0，1，…，N/2-1，于是：
　　

　　所以A(k)和B(k)可完整表示X(k)。依次类推，可一直向前追溯到2点的FFT，这样整个N点的FFT算法分解成log 2N级运算，每级有N／2个基2碟形运算。图1是N=8的DIT-FFT运算流图。
　

　　3 FFT处理器的结构设计
　　FFT实现的设计方案有顺序处理、级联处理、并行处理和阵列处理。顺序处理每次运算仅用一个蝶形单元,处理方式简单，运算速度较慢。级联处理、并行处理和阵列处理的速度较快，但占用资源较多。考虑到该设计运算点数较少，因此采用改进的顺序处理方案，在原有顺序处理的基础上对FFT处理过程中数据传输进行控制。使得该结构在继承原有顺序处理电路简单、占用资源较少优点同时又兼有级联处理运算速度较快的优点。采用自顶向下的方法对处理器模块化，其结构框图如图2所示。
　　

　　4 模块设计与综合仿真
　　整个FFT处理器是由存储器、蝶形运算单元、旋转因子单元、控制单元和数据控制单元组成，各个单元通过控制单元产生的控制和使能信号进行工作。
　　4．1 蝶形运算单元
　　蝶形运算单元是整个FFT处理单元的重要部分，直接影响整个FFT单元性能。基2时间抽取的蝶形信号流程图如图3所示，p和q为数据序号，xm(p))和xm(q)是第m级蝶形运算的输入，xm+1(p)和xm+1(q)是该蝶形运算的输出，WrN为相应的旋转因子。
　

　　采用FPGA实现FFT算法
　　由上式看出，一个基2蝶形运算要进行1次复乘、2次复加。为了提高运算速度采用并行运算，采用4个实数乘法器、3个实数加法器和3个实数减法器组成。设输入数据：x1=x1_r+jx1＿im，x2=2＿r+jx2＿im，旋转因子为WrN=c-jd，则输出y1=y1_r+jy1_im和y2=y2_r+jy2＿im。实现蝶型运算单元如图4所示。
　

　　数据格式选择定点16位二进制补码。设计时必须考虑乘法器速度，将会直接影响整个FFT处理单元的运算速度,该设计的乘法器利用QuartusⅡ开发软件中所提供的宏单元生成。乘法器的两输入均为16位，输出32位。因为乘法器中带有旋转因子项．所以乘法运算后不应改变输入的幅值即乘法器的输出仍为16位，因此要对输出数据进行截取，截取其中16位作为加(减)法器的输入。
　　4．2 存储单元
　　在FFT处理单元中存储器是必不可少的单元，蝶形运算数据的输入输出和中间结果的存储都要经过存储器，因此它们的频繁读写操作对整个FFT处理速度影响较大。图2中存储器A和存储器B由RAM和状态机组成，各自分别具有数据总线、地址总线和触发时钟。存储器A接收外部输入数据，存储器B是中间结果单元，除级蝶形运算外每级数据的输入输出均经过该存储器。在两块存储器和蝶形运算模块之间加入两个数据控制器配合工作，可以在写入上一组中间结果的同时读取下一组蝶形运算数据，从而提高FFT的处理速度。
　　4．3 旋转因子单元
　　旋转因子单元是用于存储FFT运算所需的旋转因子WrN=exp(-j2πr／N)。在Matlab中旋转因子分为实部和虚部产生，由于它们是小于1的小数，故在设计中需将其定点化。其过程是将旋转因子扩大214倍。取整数部分转化为16位定点数，以．hex文件格式保存，利用QuartusⅡ软件的Megawizard工具设计。ROM，并将．hex文件同化在其中。根据旋转因子的对称性和周期性，在利用ROM存储旋转因子时，可以只存储旋转因子表的一部分，通过地址的改变查询出每级蝶形运算所需的旋转因子。
　　4．4 控制单元
　　控制单元用于协调驱动各模块，在FFT运算中具有关键作用。存储器A、旋转因子单元及数据控制器的读信号，存储器B的读写信号都是由控制单元产生。控制单元通过一个有限状态机(FSM)实现，使用两个内部计数器控制状态机的翻转。控制单元具有单独的输入时钟，可产生相应的控制信号。
　　4．5 综合仿真
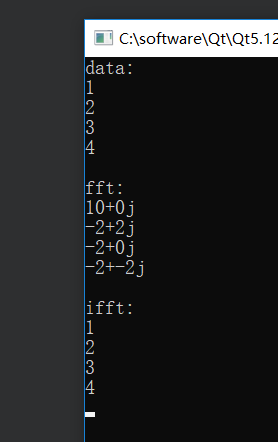
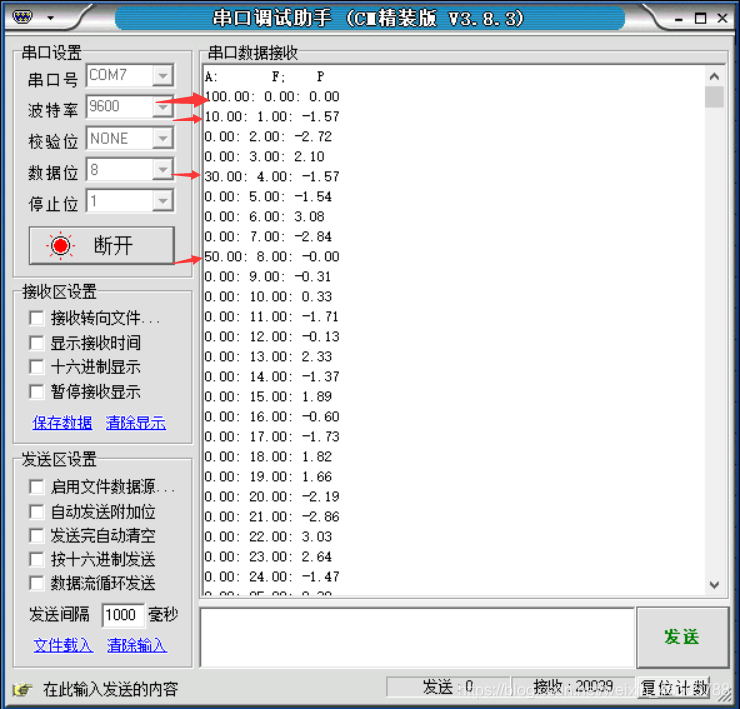
　　选用Altera公司的QuartusⅡ软件作为开发平台，以Stratix系列中的EP1S25型FPGA为器件，采用白顶向下的设计思路和VHDL语言，实现对各个模块单元的设计、综合和仿真。为了简化设计，只在数据输入时钟下输入了一组64个复数，其余输入设为0，并且实部和虚部都限定在±l，±2，±3，±4，e5之内。为防止溢出先将输入数据乘以一定比例因子2-9，再乘以2 15转化为十六进制数。输出的结果如图5所示。需要注意的是：仿真结果乘以2 -6后才是实际结果。将仿真结果与Matlab计算的结果相比较，数据基本一致，说明了设计正确，其误差主要于数据的截取和旋转因子的近似。
　

　　5 结束语
　　FFT算法是数字信号处理中一种重要运算，广泛应用于雷达、观测、跟踪、高速图像处理、保密无线通信和数字通信等领域。这里讨论了一种基于FPGA的64点FFT处理器的设计方案，输入数据的实部和虚部均以16位二进制数表示，采用基2DIT-FFT算法，以Altera公司的QuartusⅡ软件为开发平台对处理器各个的模块进行设计，在StraTIx系列中的EP1S25型FPGA通过了综合和仿真，运算结果正确。采用FPGA实现FFT算法在体积、速度、灵活性等方面都具有优越性。