前言

人生如逆旅，我亦是行人。

一、FFT

FFT（Fast Fourier Transformation），中文名快速傅里叶变换，用来 加速多项式乘法 ，就是用来降低算法的时间复杂度的，将时间复杂度由原来的 O(n^2) 变为了O(nlog2n)。

二、多项式的表示法

FFT 是一个用 O(nlog2n) 的时间将一个用 系数表示法 表示的多项式转换成用 点值表示法 表示的算法设计过程；
多项式的 系数表示 和 点值表示 可以互相转换；

系数表示法 转换成 点值表示法，结果相乘：为 求值 过程（DFT）
点值表示法 转换成 系数表示法：为 插值 过程（IDFT）

1、系数表示法

一个 n-1 次的 n 项多项式 f(x) 可以表示为：
也可以用 每一项的系数 来表示 f(x) ，即

$f(x) = { a0，a1，a2，…，an }$
是这个多项式每一项的系数

2、点值表示法

把多项式放到平面直角坐标系里面，看成一个函数；
把 n 个不同的 x 代入，会得出 n 个不同的 y ，在坐标系内就是 n 个不同的点；
点值表示
$A(x) = (x_0,f[x_0]),(x_1,f[x_1]),…, (x_n,f[x_n])$

三、高精度乘法下两种多项式表示法的区别

对于两个用系数表示的多项式

我们把它们相乘设两个多项式分别为 A ( x ) , B ( x ) ，我们要枚举 A 每一位的系数与 B 每一位的系数相乘

那么系数表示法做多项式乘法：时间复杂度 O（n^2）
点值表示法

只需要 O ( n ) 的时间

设两个点值多项式分别为：

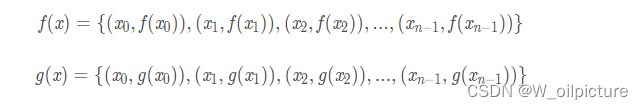
他们的乘积：

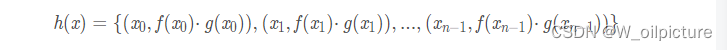
所以这里的时间复杂度只有一个枚举的 O（n）
- 但是朴素的系数表示法转点值表示法的算法还是 O（n^2）
- 朴素系数转点值的算法叫DFT（离散傅里叶变换） ，点值转系数叫 IDFT（离散傅里叶逆变换）

四、单位根的性质（！！！）

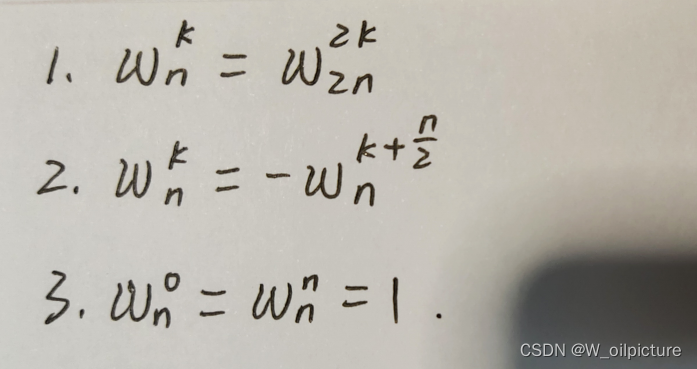
在这里插入图片描述

五、DFT（离散傅里叶变换）

一定注意从这里开始所有的 n 都默认为 2 的整数次幂

对于任意系数多项式转点值，当然可以随便取任意 n 个 x 值代入计算，但时间复杂度依然是 O(n^2)

其实可以代入一组神奇的 x ，代入以后不用做那么多的次方运算

这些 x 当然不是乱取的，而且取这些 x 值应该就是傅里叶的主意了。
规定点值中表示 n 个 x 为 n 个模长为 1 的复数，这 n 个复数不是随机的，而是 单位根。

六、FFT（快速傅里叶变换）

虽然 DFT 能把多项式转换成点值，但是它仍然是暴力代入 n 个数，并没有改变其时间复杂度，其时间复杂度仍是 O(n^2)，
因此我们可以考虑利用 单位根的性质 ，加速我们的运算，这就是 快速傅里叶变换（FFT）算法 的提出。

下面是一些步骤：（字写的一般，但写的东西很重要）

在这里插入图片描述

通过上面的步骤，我们就可以知道：
此时的时间复杂度为 O(n)

在这里插入图片描述

注：因为这一过程一定要求每层都可以分为两个大小相等的部分，所以多项式最高次项一定是 2 的幂数，不是的直接在最高次项补 0 即可。所以实际上的时间复杂度为 O(nlog2n) 。

A0(x) 和 A1(x) 都是规模缩小了一半的子问题，不断向下递归分治。

当 n = 1 时，表示只有一个常数项，直接 return ；

七、IFFT（快速傅里叶逆变换）

将两个多项式从系数表示法转化成点值表示法相乘后，还要将结果从点值表示法转化为系数表示法，也就是 IFFT（快速傅里叶逆变换） 。

重要：

把一个多项式 A(x) 的离散傅里叶变换结果（点值）作为另一个多项式 B(x) 的系数，然后再取 单位根的倒数（就是单位根的共轭复数） 作为 x 代入 B(x) 中，得到的每一项再除以 n ，最后的结果就是 A(x) 的各项系数。
这就是 傅里叶变换的逆变换 ，相当于在 FFT 的基础上在进行一次 FFT 。

八、最后的优化（迭代FFT）

在进行FFT时，我们要把各个系数不断分组并放到两侧，一个系数原来的位置和最终的位置的规律如下：
在这里插入图片描述

将每个位置用二进制表现出来，位置 x 上的数，最后所在的位置为：x 二进制翻转后得到的数字；
例如：
4（100）最后所在位置为：1（001）；
5（101）最后所在位置为：5（101），不变；
3（011）最后所在位置为：6（110）。
所以我们先把每个数放到最后的位置上，然后不断向上还原，同时求出点值表示就可以啦。
迭代版的 FFT 比之前的递归版本的更快了，真：O(nlog2n) 。

九、代码实现 FFT（C++）：

#include <bits/stdc++.h>
using namespace std;
// complex是stl自带的定义复数的容器
typedef complex<double> cp;
#define N 2097153
// pie表示圆周率π
const double pie = acos(-1);
int n;
cp a[N], b[N];
int rev[N], ans[N];
char s1[N], s2[N];
//读入优化
int read()
{int sum = 0, f = 1;char ch = getchar();while (ch > '9' || ch < '0'){if (ch == '-')f = -1;ch = getchar();}while (ch >= '0' && ch <= '9'){sum = (sum << 3) + (sum << 1) + ch - '0';ch = getchar();}return sum * f;
}
//初始化每个位置最终到达的位置
void init(int k)
{int len = 1 << k;for (int i = 0; i < len; i++)rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (k - 1));
}
// a表示要操作的系数，n表示序列长度
//若flag为1，则表示FFT，为-1则为IFFT(需要求倒数）
void fft(cp *a, int n, int flag)
{for (int i = 0; i < n; i++){// i小于rev[i]时才交换，防止同一个元素交换两次，回到它原来的位置。if (i < rev[i])swap(a[i], a[rev[i]]);}for (int h = 1; h < n; h *= 2) // h是准备合并序列的长度的二分之一{cp wn = exp(cp(0, flag * pie / h)); //求单位根w_n^1for (int j = 0; j < n; j += h * 2)  // j表示合并到了哪一位{cp w(1, 0);for (int k = j; k < j + h; k++) //只扫左半部分，得到右半部分的答案{cp x = a[k];cp y = w * a[k + h];a[k] = x + y; //这两步是蝴蝶变换a[k + h] = x - y;w *= wn; //求w_n^k}}}//判断是否是FFT还是IFFTif (flag == -1)for (int i = 0; i < n; i++)a[i] /= n;
}
int main()
{n = read();scanf("%s%s", s1, s2);//读入的数的每一位看成多项式的一项，保存在复数的实部for (int i = 0; i < n; i++)a[i] = (double)(s1[n - i - 1] - '0');for (int i = 0; i < n; i++)b[i] = (double)(s2[n - i - 1] - '0');// k表示转化成二进制的位数int k = 1, s = 2;while ((1 << k) < 2 * n - 1)k++, s <<= 1;init(k);// FFT 把a的系数表示转化为点值表示fft(a, s, 1);// FFT 把b的系数表示转化为点值表示fft(b, s, 1);// FFT 两个多项式的点值表示相乘for (int i = 0; i < s; i++)a[i] *= b[i];// IFFT 把这个点值表示转化为系数表示fft(a, s, -1);//保存答案的每一位(注意进位）for (int i = 0; i < s; i++){//取实数四舍五入，此时虚数部分应当为0或由于浮点误差接近0ans[i] += (int)(a[i].real() + 0.5);ans[i + 1] += ans[i] / 10;ans[i] %= 10;}while (!ans[s] && s > -1)s--;if (s == -1)printf("0");elsefor (int i = s; i >= 0; i--)printf("%d", ans[i]);return 0;
}