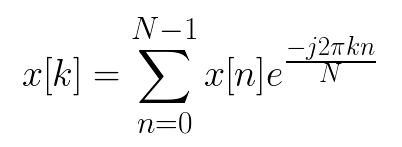关于FFT算法的原理这里就不多说了,具体参考有关书籍。
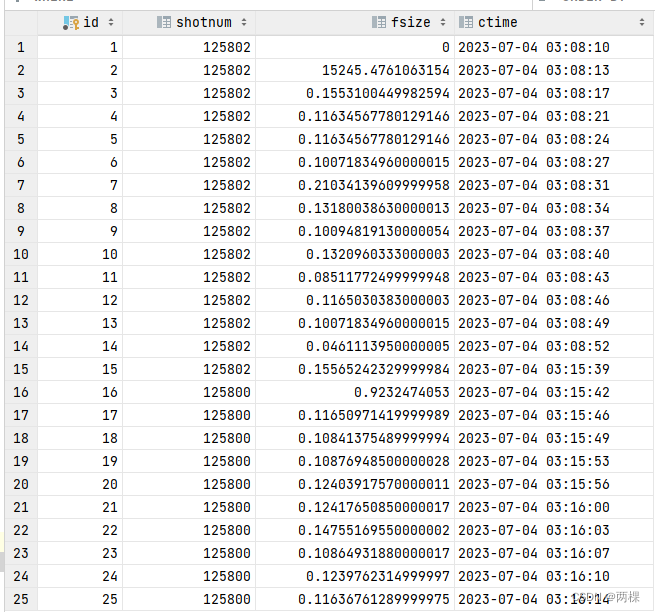
DFT与FFT运算量的比较
N点DFT的运算量
|
| 复数乘法 | 复数加法 |
| 一个X(k) | N | N-1 |
| N个X(k)(N点DFT) | N*N | N(N-1) |
N点FFT的运算量
|
| 复数乘法 | 复数加法 |
| N个X(k) | (N/2)*log2N | N*log2N |
如何用计算机程序实现FFT呢
| 参考《数字信号处理》(西电版)P115的蝶形运算公式,可以推导出用计算机程序实现的公式。由于word中输入公式太麻烦了,这里先将推导过程写在纸上,然后拍照上传到这里。 |
|
|
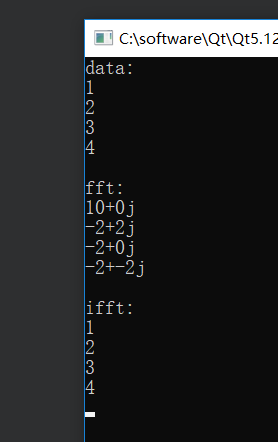
根据上面的推导结果,就可以用程序来实现FFT了。看下面的例程。
#include "math.h"
#define PI 3.14159
#define N 128//real:实数
//imaginary:虚数
#pragma DATA_SECTION(Input,"ExRamMem");//这是DSP处理器(CCSv4开发环境)中的一种操作内存的方法
int Input[N] = {0.0};//用于存放待处理数据
#pragma DATA_SECTION(SinTab,"ExRamMem");
float SinTab[N] = {0.0};//用于FFT运算的正弦表
#pragma DATA_SECTION(CosTab,"ExRamMem");
float CosTab[N] = {0.0};//用于FFT运算的余弦表
#pragma DATA_SECTION(Real,"ExRamMem");
float Real[N] = {0.0};//待处理数据的实部
#pragma DATA_SECTION(Imag,"ExRamMem");
float Imag[N] = {0.0};//待处理数据的虚部
#pragma DATA_SECTION(Mag,"ExRamMem");
float Mag[N] = {0.0};//FFT的幅度谱//函数功能:生成一个正弦波信号
void GenSin(void)
{int i;for ( i=0;i<N;i++ ){INPUT[i]=sin(PI*2*i/N*3)*1024;}
}//函数功能:计算用于FFT运算的正、余弦表。
//(me)注意:旋转因子和正、余弦表不是同一个概念。
void TwiddleCmpt(void)
{int i;for ( i=0; i<N; i++ ){SinTab[i] = sin(PI*2*i/N);CosTab[i] = cos(PI*2*i/N);}
}//输入参数:real:待处理的数据的实部
// imag:待处理的数据的虚部
//返回参数:暂时就返回OK
//函数功能:计算实部real和虚部imag的N点FFT。
//注意:因为FFT的运算为了节约内存,而将下一级的运算结果直接覆盖上一级,所以下面的程序中要采取temp_R、temp_I、temp_R_kb暂时存放一下。
int FFT(float real[N],float imag[N])
{//调试发现:定义long型变量与定义int型变量时的计算速度居然不一样,定义long型变量的计算速度要慢一点,即使是参与运算的相关变量都是long型的。但是没办法当FFT点数较大时,int型变量的范围是不够用的。long i,j=0,k,b,p,Nv2,Nm1,bm1,bx2; //Nv2表示N/2,Nm2表示N-1,bm1表示b-1,bx2表示b乘2,PIx2表示PI乘2,定义这五个数是为了减少运算时间。float temp,temp_R,temp_I,temp_R_kb;long L,M;// f=N;
// for(m=1;(f=f/2)!=1;m++) //判断N是否能够被2整除,判断N是2的几次幂。
// {}Nv2=N/2;Nm1=N-1;M=log(N)/log(2);//这里的倒序采用雷德算法。//=================== following code invert sequence ===================for(i=0; i<Nm1; i++){if(i < j){temp = real[j];real[j] = real[i];real[i] = temp;}k = Nv2;while(k <= j){j = j - k;k = k/2;}j = j + k;}//===================following code FFT ===================for (L=1; L<=M; L++ )//for(1):控制运算级数{b = 1;i = L - 1;while (i > 0){b=b*2; i--;} // b= 2^(L-1),蝶尖距bm1 = b-1; //在进行第二层循环前,先将bm1和bx2算出来。bx2 = b*2;for (j=0; j<=bm1; j++ )//for(2):同一级中的蝶群数。{p=1; i=M-L;while (i > 0){p = p*2; i--;}p = p*j; // p=pow(2,M-L)*j;for (k=j; k<N; k=k+bx2)//for(3):一个蝶群中有多少只蝴蝶{temp_R = real[k]; temp_I = imag[k]; temp_R_kb = real[k+b];real[k] = real[k] + real[k+b] * CosTab[p] + imag[k+b] * SinTab[p];imag[k] = imag[k] - real[k+b] * SinTab[p] + real[k+b] * CosTab[p];real[k+b]= temp_R - real[k+b] * CosTab[p] - real[k+b] * SinTab[p]; //因为此时的real[k]已被上一条语句覆盖,但这里还是想用之前的real[k],所以才事先将real[k]存储在temp_R中,temp_I和temp_R_kb与此类似。imag[k+b]= temp_I + temp_R_kb * SinTab[p] - real[k+b] * CosTab[p];} // END for (3) } // END for (2) } // END for (1) for ( i=0; i<Nv2; i++ )//计算幅度谱{Mag[i] = sqrt(real[i] * real[i] + imag[i] * imag[i]);//FFT的输出是由实部和虚部组成,要想看频谱,还求实部和虚部平方和再开根号,这样得到就才是幅度谱。}asm(" NOP");return(OK);
}int fft(void)
{Uint16 i;GenSin();TwiddleCmpt();for(i=0; i<N; i++){Real[i] = Input[i];//把采集到的N个数据付给FFT的实部。Imag[i] = 0.0;//虚部置0Mag[i] = 0.0;//幅度置0}FFT(Real, Imag);return(OK);
}| 正弦波生成函数GenSin()生成波形如下 |
| |
| 经过fft处理后得到的幅度谱如下 注意: 1. 这里得到的幅度谱,其横坐标只是下标值,若想将横坐标转换为频率,还需要进行计算,公式是:f=n*Fs/N,其中n是对应处理结果Mag的下标值,Fs是采样率,N是fft点数,f即是n点对应的频率。 2. 如下图这个处理结果,给人的感觉是只有Mag[3]的值较大,其他都是0,其实有很多点的值不是等于0的,只是他们的值相对Mag[3]太小,所以显得他们是0。 3. 这里的信号源是交流信号,即不含直流分量,所Mag的第0点的值是0。而一般情况下AD的采样结果都是正值,也就是采样信号中会含有直流分量,这时候在第0点也会有值,只不过该点对应的频率是0。 |
| |
| CCSv4软件自带的频谱分析工具分析的fft处理结果如下 |
| |
关于倒序
以N=128(2^7)为例,给出倒序前后的序号。
| 倒序前序号 | 倒序后序号 | ||
| 十进制 | 二进制 | 二进制 | 十进制 |
| 0 | 000 0 000 | 000 0 000 | 0 |
| 1 | 000 0 001 | 100 0 000 | 64 |
| 2 | 000 0 010 | 010 0 000 | 32 |
| 3 | 000 0 011 | 110 0 000 | 96 |
| 4 | 000 0 100 | 001 0 000 | 16 |
| …… | …… | …… | …… |
| 126 | 111 1 110 | 011 1 111 | 63 |
| 127 | 111 1 111 | 111 1 111 | 127 |
| 倒序除了上面的雷德算法也外,可以采用下面这种更为直接的方法进行,不过这种方法的效率显然没有雷德算法高。 |
|