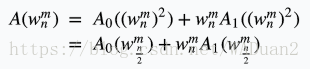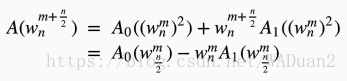FFT——快速傅里叶变换
这块不写东西空荡荡的,我决定还是把FFT的定义给贴上吧
FFT(Fast Fourier Transformation)是离散傅氏变换(DFT)的快速算法。即为快速傅氏变换。它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。
这三段话其实一点用也没有
FFT是干什么的
FFT在算法竞赛中就有一个用途:加速多项式乘法(暴言)
简单来说,形如 a 0 X 0 + a 1 X 1 + a 2 X 2 + ⋯ + a n X n a_0X^0+a_1X^1+a_2X^2+⋯+a_nX^n a0X0+a1X1+a2X2+⋯+anXn 的代数表达式叫做多项式,可以记作 f ( X ) = a 0 X 0 + a 1 X 1 + a 2 X 2 + ⋯ + a n X n f(X)=a_0X^0+a_1X^1+a_2X^2+⋯+a_nX^n f(X)=a0X0+a1X1+a2X2+⋯+anXn,其中 a 0 , a 1 , ⋯ , a n a_0,a_1,⋯,a_n a0,a1,⋯,an叫做多项式的系数, X X X是一个不定元(就是不可以合并),不表示任何值,不定元在多项式中最大项的次数称作多项式的次数
如果我们当前有两个多项式 f ( X ) , g ( X ) f(X),g(X) f(X),g(X),现在要把他们乘起来(求卷积),最朴素的做法就是
∑ i = 0 2 n − 1 ( ∑ j = 0 i a j ∗ b i − j ) ∗ x i \sum \limits _{i=0}^{2n-1} (\sum \limits _{j=0} ^{i} a_j*b_{i-j})*x^i i=0∑2n−1(j=0∑iaj∗bi−j)∗xi
这样的复杂度是 Θ ( n 2 ) \varTheta(n^2) Θ(n2)的,十分不美观,FFT就是要将这个过程优化为 Θ ( n log n ) \varTheta(n \log n) Θ(nlogn)
前置技能
多项式
见上文
复数
复数形如 a + b i a+bi a+bi,其中 i = − 1 i=\sqrt {-1} i=−1
a a a叫作复数的实部, b i bi bi叫做复数的虚部
复数 ( a 1 + b 1 i ) ∗ ( a 2 + b 2 i ) (a_1+b_1i)*(a_2+b_2i) (a1+b1i)∗(a2+b2i)相乘的值,即 a 1 a 2 − b 1 b 2 + ( a 1 b 2 + a 2 b 1 ) i a_1a_2-b_1b_2+(a_1b_2+a_2b_1)i a1a2−b1b2+(a1b2+a2b1)i也是一个复数,同时我们也得到了复数的乘法法则
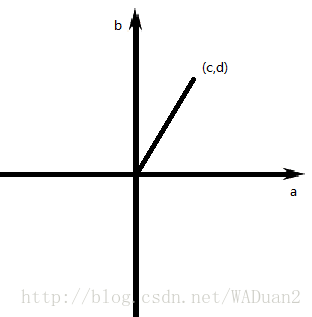
复数 c + d i c+di c+di可以用这种方式表示出来
复数乘法的在复平面中表现为辐角相加,模长相乘
单位根
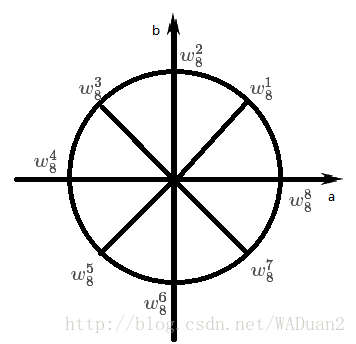
复数 w w w满足 w n = 1 w^n=1 wn=1称作 w w w是 n n n次单位根,下图包含了所有的 8 8 8次单位根(图中圆的半径是1)
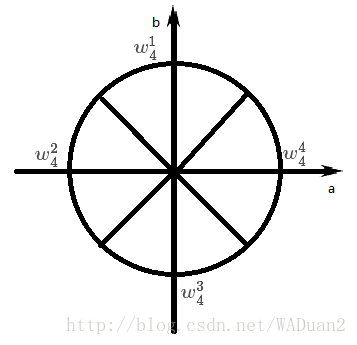
同样的,下图是所有的4次单位根
聪明的你也许已经发现了单位根的些许性质,即
w 2 n 2 m = w n m w_{2n}^{2m}=w_{n}^{m} w2n2m=wnm
w n m = − w n m + n 2 w_n^m=-w_n^{m+\frac{n}{2}} wnm=−wnm+2n
这两个要记住,一会很有用
多项式的系数表达法
我们有多项式 f ( X ) = a 0 X 0 + a 1 X 1 + a 2 X 2 + ⋯ + a n X n f(X)=a_0X^0+a_1X^1+a_2X^2+⋯+a_nX^n f(X)=a0X0+a1X1+a2X2+⋯+anXn,令 a ⃗ = ( a 0 , a 1 , a 2 , . . . , a n ) \vec{a}=(a_0,a_1,a_2,...,a_n) a=(a0,a1,a2,...,an),则称 A ( X ) A(X) A(X)为多项式 f ( X ) f(X) f(X)的系数表示法
在系数表示法下,计算多项式乘法是 Θ ( n 2 ) \varTheta (n^2) Θ(n2)的
多项式的点值表达法
任取 n + 1 n+1 n+1个互不相同的 S = { p 1 , p 2 , . . . , p n + 1 } S=\{p_1,p_2,...,p_{n+1}\} S={p1,p2,...,pn+1},对 f ( X ) f(X) f(X)分别求值得到 f ( p 1 ) , f ( p 2 ) , . . . , f ( p n + 1 ) f(p_1),f(p_2),...,f(p_{n+1}) f(p1),f(p2),...,f(pn+1),那么称 A ( X ) = { ( p 1 , f ( p 1 ) ) , ( p 2 , f ( p 2 ) ) , . . . , ( p n + 1 , f ( p n + 1 ) ) } A(X)=\{(p_1,f(p_1)),(p_2,f(p_2)),...,(p_{n+1},f(p_{n+1}))\} A(X)={(p1,f(p1)),(p2,f(p2)),...,(pn+1,f(pn+1))}为多项式 f ( X ) f(X) f(X)在 S S S下的点值表示法
可以把多项式想象成一个 n n n次函数,点值表示法就是取 S S S下每一个横坐标时对应的点,因为 n n n次函数可以由 n + 1 n+1 n+1个点确定下来(可以将每一个点列一个 n n n次方程),所以 n n n维点值与 n n n维系数一一对应
更重要的一点,点值表示法下的乘法运算获得了简化
两个多项式 P P P, Q Q Q分别取点 ( x , y 1 ) (x,y_1) (x,y1)和 ( x , y 2 ) (x,y_2) (x,y2), P ∗ Q P*Q P∗Q就会取到点 ( x , y 1 ∗ y 2 ) (x,y_1*y_2) (x,y1∗y2);
令 C = P ∗ Q C=P*Q C=P∗Q,因为 C ( X ) = P ( X ) ∗ Q ( X ) C(X)=P(X)*Q(X) C(X)=P(X)∗Q(X),所以 C ( x ) = P ( x ) ∗ Q ( x ) C(x)=P(x)*Q(x) C(x)=P(x)∗Q(x),即 C ( x ) = y 1 ∗ y 2 C(x)=y_1*y_2 C(x)=y1∗y2
所以在点值表示法下,计算多项式乘法是 Θ ( n ) \varTheta(n) Θ(n)的
FFT的具体过程
FFT就是将系数表示法转化成点值表示法相乘,再由点值表示法转化为系数表示法的过程,第一个过程叫做求值(DFT),第二个过程叫做插值(IDFT)
求值
还记得我们之前提到的单位根吗?再回顾一下:
w 2 n 2 m = w n m w_{2n}^{2m}=w_{n}^{m} w2n2m=wnm
w n m = − w n m + n 2 w_n^m=-w_n^{m+\frac{n}{2}} wnm=−wnm+2n
想要求出一个多项式的点值表示法,需要选出 n + 1 n+1 n+1个数分别带入到多项式里面,带入一个数的复杂度是 Θ ( n ) \varTheta(n) Θ(n)的,那么总复杂度就是 Θ ( n 2 ) \varTheta(n^2) Θ(n2)的,因为单位根有上面两个优美的性质,所以我们尝试可以取 n n n次单位根组成 S S S,看看能不能加速我们的运算
设 A 0 ( X ) A_0(X) A0(X)为 A ( X ) A(X) A(X)偶次项的和,设 A 1 ( X ) A_1(X) A1(X)为 A ( X ) A(X) A(X)奇次项的和,即
A 0 ( X ) = a 0 x 0 + a 2 x 1 + . . . + a n − 1 x n / 2 A_0(X)=a_0x^0+a_2x^1+...+a_{n-1}x^{n/2} A0(X)=a0x0+a2x1+...+an−1xn/2
A 1 ( X ) = a 1 x 0 + a 3 x 1 + . . . + a n − 2 x n / 2 A_1(X)=a_1x^0+a_3x^1+...+a_{n-2}x^{n/2} A1(X)=a1x0+a3x1+...+an−2xn/2
因为 A ( w n m ) = a 0 w n 0 + a 1 w n m + a 2 w n 2 m + a 3 w n 3 m + . . . + a n − 1 w n ( n − 1 ) ∗ m + a n w n n m A(w_n^m)=a_0w_n^0+a_1w_n^m+a_2w_n^{2m}+a_3w_n^{3m}+...+a_{n-1}w_n^{(n-1)*m}+a_nw_n^{nm} A(wnm)=a0wn0+a1wnm+a2wn2m+a3wn3m+...+an−1wn(n−1)∗m+anwnnm
所以有
也就是说,只要有了 A 0 ( X ) A_0(X) A0(X)和 A 1 ( X ) A_1(X) A1(X)的点值表示,就能在 Θ ( n ) \varTheta(n) Θ(n)时间算出 A ( X ) A(X) A(X)的点值表示,对于当前层确定的位置 i i i,就可以用下一层的两个值更新当前的值,我们称这个操作为“蝴蝶变换”
因为这个过程一定要求每层都可以分成两大小相等的部分,所以多项式最高次项一定是 2 p 2^p 2p( p ∈ N p\in N p∈N)次方,如果不是的话,直接在最高次项补零就可以啦
于是我们有了递归的写法:
void FFT(Complex* a,int len){if(len==1) return;Complex* a0=new Complex[len/2];Complex* a1=new Complex[len/2];for(int i=0;i<len;i+=2){a0[i/2]=a[i];a1[i/2]=a[i+1];}FFT(a0,len/2);FFT(a1,len/2);Complex wn(cos(2*Pi/len),sin(2*Pi/len));Complex w(1,0);for(int i=0;i<(len/2);i++){a[i]=a0[i]+w*a1[i];a[i+len/2]=a0[i]-w*a1[i];w=w*wn;}return;
}
但递归版的FFT常数巨大,实现起来比较复杂,于是又有了迭代的写法
重新考虑下递归FFT的过程,在第 i i i次求解中,我们将所有元素二进制 i i i位为 0 0 0的放在了左面, i i i位为 1 1 1的放在了右面,事实上,每个元素最终到的是他二进制颠倒过来的位置
再拿一张别人的图
迭代写法:
inline void DFT(Complex a[]){for(int i=0;i<len;i++)///pos[i]代表反转后的位置if(i<pos[i])swap(a[i],a[pos[i]]);for(int i=2,mid=1;i<=len;i<<=1,mid<<=1){///len代表多项式最高次项///第一层i是枚举合并到了哪一层。Complex wm(cos(2.0*pi/i),sin(2.0*pi/i));for(int j=0;j<len;j+=i){///第二层j是枚举合并区间。Complex w(1,0);for(int k=j;k<j+mid;k++,w=w*wm){///第三层k是枚举区间内的下标。Complex l=a[k],r=w*a[k+mid];a[k]=l+r;a[k+mid]=l-r;}}}return;
}
插值
有人证出来插值只要将所有 w n m w_n^m wnm换成 w n m + n 2 w_n^{m+\frac{n}{2}} wnm+2n,也就是所有的虚部取相反数,再将最终结果除以 l e n len len,就是插值的过程了
究竟为什么?我觉得人生一定要有点遗憾可以参考这里,我就不多说了
支持插值的迭代写法:
const double DFT=2.0,IDFT=-2.0;///进行求值,第二个参数传DFT,插值传IDFT
inline void FFT(Complex a[],double mode){for(int i=0;i<len;i++)if(i<pos[i])swap(a[i],a[pos[i]]);for(int i=2,mid=1;i<=len;i<<=1,mid<<=1){Complex wm(cos(2.0*pi/i),sin(mode*pi/i));for(int j=0;j<len;j+=i){Complex w(1,0);for(int k=j;k<j+mid;k++,w=w*wm){Complex l=a[k],r=w*a[k+mid];a[k]=l+r;a[k+mid]=l-r;}}}if(mode==IDFT)for(int i=0;i<len;i++)a[i].x/=len;return;
}
现在,你已经会写FFT了!
生成函数
小 A A A有 a i a_i ai个价值为 A i A_i Ai的物品,小 B B B有 b i b_i bi个价值为 A i A_i Ai的物品,求用两个组成价值为 c i c_i ci的方案数
生成函数可以解决上面的这个问题,构造两个多项式,第 i i i项表示价值为 i i i的物品有多少个,对两个人分别构造,乘在一起的多项式就代表所有的方案数了
NTT——快速数论变换
当FFT需要取模时,复数的存在就特别尴尬了,有没有什么东西可以代替单位根呢?
原根性质:假设 g g g是素数 p p p的一个原根,则 g 1 , g 2 , . . . , g ( p − 1 ) g^1,g^2,...,g^{(p-1)} g1,g2,...,g(p−1)在模 p p p意义下两两不同,且结果恰好为 1 1 1~ p − 1 p-1 p−1
w n n ≡ g ( p − 1 ) ≡ 1 ( m o d p ) w_n^n≡g^{(p-1)}≡1(mod\ p) wnn≡g(p−1)≡1(mod p)(中间那个是费马小定理)
所以可以把 g ( p − 1 ) / n g^{(p-1)/n} g(p−1)/n看成 w n 1 w_n^1 wn1的等价。
但这种质数必须是NTT质数(费马质数),即 ( p − 1 ) (p-1) (p−1)有超过序列长度的2的正整数幂因子的质数
具体证明还是看这里吧
参考资料:
Pick’s blog
Fenghr的博客
Miskcoo’s Space