使用python手写FFT算法

article/2025/10/18 22:09:49

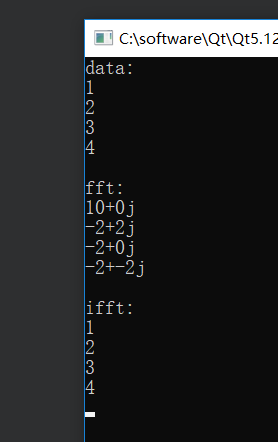
FFT(Fast Fourier Transform) 是 DFT(Discrete Fourier Transform)的快读实现，它在机理上没有改变DFT的算法，只是在实现上采用的巧妙的实现。使 $O(N^2)$ 的实现变成了 $O(Nlog_2N)$ 的实现，优化算法的复杂度。

DFT 公式

DFT的公式我们先简单回忆一下：

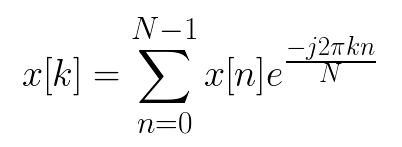
DFT公式

DFT的python实现

def dft(x):x = np.asarray(x, dtype=float)N = x.shape[0]n = np.arange(N)k = n.reshape((N, 1))M = np.exp(-2j * np.pi * k * n / N)return np.dot(M, x)x = np.random.random(1024)
np.allclose(dft(x), np.fft.fft(x))

FFT的思想其实分而治之，将整个DFT安装奇偶来分开计算

FFT之奇偶分治

首先根据DFT公式，将x分为odd(奇数),下标用2r+1表示；和even(偶数)下标用2r表示
$X_k = \sum_{n=0}^{N-1} x_n e^{\frac{-j2{\pi}kn}{N}} \newline = \sum_{n=0}^{\frac{N}{2}-1} x_{2r+1} e^{\frac{-j2{\pi}k(2r+1)}{N}} + \sum_{n=0}^{\frac{N}{2}-1} x_{2r} e^{\frac{-j2{\pi}k(2r)}{N}} \newline = \sum_{n=0}^{\frac{N}{2}-1} x_{2r+1} e^{\frac{-j4{\pi}kr}{N}} e^{\frac{-j2{\pi}k}{N}} + \sum_{n=0}^{\frac{N}{2}-1} x_{2r} e^{\frac{-j4{\pi}kr}{N}} \newline = \sum_{n=0}^{\frac{N}{2}-1} x_{2r+1} e^{\frac{-j2{\pi}kr}{N/2}} e^{\frac{-j2{\pi}k}{N}} + \sum_{n=0}^{\frac{N}{2}-1} x_{2r} e^{\frac{-j{2\pi}kr}{N/2}} \newline = e^{\frac{-j2{\pi}k}{N}} X_{odd} + X_{even}$

python实现

1. 根据奇偶分治和迭代的方式实现

def fft(x):x = np.asarray(x, dtype=float)N = x.shape[0]if N % 2 > 0:raise ValueError("must be a power of 2")elif N <= 2:return dft(x)else:X_even = fft(x[::2])X_odd = fft(x[1::2])terms = np.exp(-2j * np.pi * np.arange(N) / N)return np.concatenate([X_even + terms[:int(N/2)] * X_odd,X_even + terms[int(N/2):] * X_odd])
x = np.random.random(1024)
np.allclose(fft(x), np.fft.fft(x))

2. 使用矩阵运算加速

def fft_v(x):x = np.asarray(x, dtype=float)N = x.shape[0]if np.log2(N) % 1 > 0:raise ValueError("must be a power of 2")N_min = min(N, 2)n = np.arange(N_min)k = n[:, None]M = np.exp(-2j * np.pi * n * k / N_min)X = np.dot(M, x.reshape((N_min, -1)))while X.shape[0] < N:X_even = X[:, :int(X.shape[1] / 2)]X_odd = X[:, int(X.shape[1] / 2):]terms = np.exp(-1j * np.pi * np.arange(X.shape[0])/ X.shape[0])[:, None]X = np.vstack([X_even + terms * X_odd,X_even - terms * X_odd])
return X.ravel()