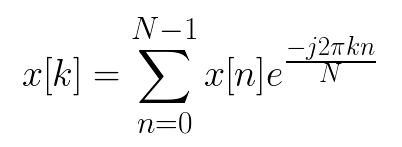FFT算法实践报告

FFT基本原理

代码链接: link.

DFT

在讨论FFT之前，我们需要先了解以下DFT。所谓的DFT其实就是两个矩阵做点乘。
多项式可以有两种表示方法，一种是系数表示法，另一种是点值表示法。
这两种表示法之间是可以转换的，系数表示法到点值表示法非常简单，就是随便取几个点带入求值，而点值表示法到系数表示法就需要用到插值法，关于插值法又不在本文的讨论范围之内了。
所谓的点值表示法，设A(x)是一个n阶的多项式，那么至少可以用n+1对(x0,A(x0)),(x1,A(x1))…这样的点对来表示，也就是说确定了这n+1个点，就可以唯一的确定一个多项式，形如a0+a1x+a2x²+…这种。证明的方法利用到了幼儿园级别的线性代数知识。
当两个多项式相乘时，我们可以很自然的想到将对应的点值相乘，这样就得到了结果的点值表示法。
假设现在有两个n阶的多项式相乘，那么利用点值表示法，我们需要将对应的n个点分别相乘，也就是要做n*n次乘法运算，这个时间复杂度是O(n²),与我们直接将系数表示下的多项式相乘复杂度一致。

这已经是离散傅里叶变化的思想了。
所谓离散傅里叶变换就是

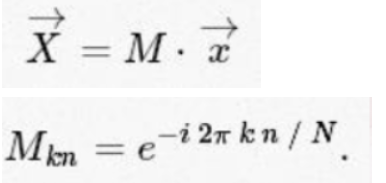
其本质就是M矩阵和X向量做点乘。

FFT

我们想要找到突破口就需要在将多项式转化为点值表示这一步做一点小操作。这一点操作就是利用对称性，减少计算量。
我们注意到一个n阶多项式A(x) = a0+a1x²+a2x³+…其奇数项是奇函数，偶数项是偶函数。而奇数项又可以分离成x乘一个偶函数。
因此，我们利用偶函数的性质可以减少很多计算量。

比方现在有一个多项式x+x²+x³，那么我们应该至少需要4对点才可以求得该多项式的点值表示法，我可以找x1,x2,-x1,-x2这样的正负对，所以只需要找2对即可，因为另一半的值就无非就是符号不同。
但是只是这样的一次对称只能减少一半的计算量，只能让原本O(n²)的算法变为O(n²/2)，其提升不是很大。如果可以一直利用这种对称性就好了，这种对称性建立的前提是正负对的存在，但是显然在实数域我们无法做到这一点，所以必须要在复数域讨论。
所以Fourier提出，对于一个n-1阶的多项式，我们不妨直接用n个复数w0,w1,w2…wn代替原来的x0,x1,x2…xn，这样得到一种特殊的点值表示法就是被成为离散傅里叶变化(DFT)。而这n个复数不是随便选取的，而是在复平面将单位圆等分n分后对应的点。

单位根的性质复平面上的单位根有这样一个性质

于是正负对出现了。
我们的程序就可以按照这个框架来写了。

python实现

DFT

#DFT，本质就是两个矩阵相乘
def DFT(x):x = np.asarray(x,dtype=float)N = x.shape[0]M = [[j for i in range(N)]for j in range(N)]M = np.asarray(M,dtype=complex)w = np.exp(-2j*np.pi/N)for i in range(N):for j in range(N):M[i][j] = np.power(w,i*j)return np.dot(M,x)

FFT

递归

#递归FFT，利用分治思想的dft
def fft_recurrence(x):x = np.asarray(x,dtype=float)N = x.shape[0]if N<2:return DFT(x)x_even = fft_recurrence(x[0::2])x_odd = fft_recurrence(x[1::2])factor = np.exp(-2j * np.pi * np.arange(N) / N)return np.concatenate([x_even + factor[:int(N / 2)] * x_odd,x_even + factor[int(N / 2):] * x_odd])

非递归

上面那种FFT是最基础的，同时因为递归的原因执行速度很慢，所以提出了非递归的优化方法。
观察 n =4时候的子序列位置变换情况

我们发现子序列最终的位置其实就是初始位置的二进制翻转后结果，如3(11)变为了3(11)，而1(01)变为了2(10)。

Java实现

Complex复数类

首先创建一个复数类，定义一系列的加减乘除操作。

package fft;public class Complex {private double realPart;private double imaginaryPart;public Complex() {this.realPart =0;this.imaginaryPart =0;}public Complex(double realPart,double imaginaryPart) {this.realPart = realPart;this.imaginaryPart = imaginaryPart;}/*** 加法运算* @param w* @return*/public Complex add(Complex w) {if (w ==null) {return new Complex();}return new Complex(this.realPart+w.getRealPart(),this.imaginaryPart+w.getImaginaryPart());}/*** 减法运算* @param w* @return*/public Complex subt(Complex w) {if (w ==null) {return new Complex();}return new Complex(this.realPart-w.getRealPart(),this.imaginaryPart-w.getImaginaryPart());}/***乘法 * @param w* @return*/public Complex mult(Complex w) {if (w ==null) {return new Complex();}return new Complex(this.realPart*w.getRealPart()-this.imaginaryPart*w.getImaginaryPart(),this.realPart*w.getImaginaryPart()+this.imaginaryPart*w.getRealPart());}/*** 除法* @param w* @return*/public Complex divide(Complex w) {if (w ==null) {return new Complex();}double W = w.getImaginaryPart()*w.getImaginaryPart() - w.getRealPart()*w.getRealPart();return new Complex((this.realPart*w.getRealPart()+this.imaginaryPart*w.getImaginaryPart())/W,(this.imaginaryPart*w.getRealPart()-this.realPart*w.getImaginaryPart())/W);}@Overridepublic String toString() {// TODO Auto-generated method stubString s = (this.imaginaryPart>=0)? "+":"";return this.realPart+s+this.imaginaryPart+"i";}/*** @return the realPart*/public double getRealPart() {return realPart;}/*** @param realPart the realPart to set*/public void setRealPart(double realPart) {this.realPart = realPart;}/*** @return the imaginaryPart*/public double getImaginaryPart() {return imaginaryPart;}/*** @param imaginaryPart the imaginaryPart to set*/public void setImaginaryPart(double imaginaryPart) {this.imaginaryPart = imaginaryPart;}}

Matrix复数矩阵类

Matrix类是一个复数矩阵类，定义了一系列我们要用到的矩阵操作

package fft;/**复数矩阵* @author zhangx**/
public class Matrix {/**** 对矩阵进行切片，只能切列向量* @param a* @param x1 begin* @param x2 end* @return*/public static Complex[][] subMatrix(Complex[][] a,int x1,int x2){int n = a.length;int m = a[0].length;int l = x2-x1;Complex[][] b = new Complex[l][m];for(int i =0;i<l;)for(int j =0;j<n;j++)if(j>=x1&&j<x2)b[i++] = a[j];return b;}/*** 矩阵切片升级版，可以切任意矩形形状* @param a* @param x1* @param x2* @param y1* @param y2* @return*/public static Complex[][] subMatrix(Complex[][] a,int x1,int x2,int y1,int y2){int n = a.length;int m = a[0].length;int l = x2-x1;int d = y2-y1;Complex[][] b = new Complex[l][d];for(int i =0;i<l;) {for(int k=0;k<n;k++) {if(k>=x1&&k<x2) {for(int j=0;j<d;) {for(int p =0;p<m;p++) {if(p>=y1&&p<y2) {b[i][j] = a[k][p];j++;}}}i++;}}}return b;}/**** 返回偶数序列* @param a* @return*/public static Complex[][] evenMatrix(Complex[][] a){int n =a.length;int m = a[0].length;int l = n/2;Complex[][] b = new Complex[l][m];for(int i =0;i<l;i++)b[i] = a[2*i];return b;}/**** 返回奇数序列* @param a* @return*/public static Complex[][] oddMatrix(Complex[][] a){int n =a.length;int m = a[0].length;int l = n/2;Complex[][] b = new Complex[l][m];for(int i =0;i<l;i++)b[i] = a[2*i+1];return b;}/*** 粘结矩阵* @param a* @param b* @return*/public static Complex[][] concatenate(Complex[][] a,Complex[][] b){int na = a.length;int ma = a[0].length;int nb = b.length;int mb = b[0].length;//维度不同不可以粘接if(ma!=mb)return null;Complex[][] c = new Complex[na+nb][ma];for(int i =0;i<c.length;i++)c[i] = (i>=na)? b[i-na]:a[i];return c;}/*** 打印矩阵* @param a*/public static void show(Complex[][] a) {for (int i =0;i<a.length;i++) {for (Complex j:a[i]) {System.out.print(j.toString()+" ");}System.out.println();}}/*** 矩阵相加* @param a* @param b* @return*/public static Complex[][] mAdd(Complex[][] a,Complex[][] b){int na = a.length;int ma = a[0].length;int nb = b.length;int mb = b[0].length;//维度不同不可想加if(na!=nb||ma!=mb)return null;Complex[][] c = new Complex[na][ma];for(int i =0;i<na;i++)for(int j =0;j<ma;j++) c[i][j] = a[i][j].add(b[i][j]);return c;}/*** 按位置相乘矩阵* @param a* @param b* @return*/public static Complex[][] lMult(Complex[][] a ,Complex[][] b){int n = a.length;int m =b.length;if(n!=m)return null;Complex[][] c = new Complex[n][a[0].length];for(int i =0;i<n;i++)for(int j=0;j<a[0].length;j++) {c[i][j] = a[i][j].mult(b[i][j]);}return c;}/*** 复数矩阵乘法* @param a* @param b* @return*/public static Complex[][] mMult(Complex[][] a,Complex[][] b) {//当a的列数与矩阵b的行数不相等时，不能进行点乘，返回nullif (a[0].length != b.length)return null;//c矩阵的行数y，与列数xint y = a.length;int x = b[0].length;Complex c[][] = new Complex[y][x];//初始化c矩阵for (int i =0;i<c.length;i++)for (int j=0;j<c[0].length;j++) {c[i][j] = new Complex(0,0);}//运算主体部分for (int i = 0; i < y; i++)for (int j = 0; j < x; j++)//c矩阵的第i行第j列所对应的数值，等于a矩阵的第i行分别乘以b矩阵的第j列之和for (int k = 0; k < b.length; k++)c[i][j] =c[i][j].add(a[i][k].mult(b[k][j]));return c;}public static void main(String[] args) {Complex[][] a =new Complex[4][3];Complex[][] b =new Complex[4][3];for (int i =0;i<a.length;i++)for (int j =0;j<a[0].length;j++) {a[i][j] = new Complex(i,j);}for (int i =0;i<b.length;i++)for (int j =0;j<b[0].length;j++) {b[i][j] = new Complex(i,0);}Complex[][] c = new Complex[a.length][b[0].length];for (int i =0;i<c.length;i++)for (int j=0;j<c[0].length;j++) {c[i][j] = new Complex(0,0);}
//		c = Matrix.subMatrix(a, 2, 4);
//		c = Matrix.oddMatrix(a);Matrix.show(a);Complex[][] d = Matrix.subMatrix(a, 1, 3, 1, 2);System.out.println();Matrix.show(d);//		c = Matrix.mMult(a, b);
//		
//		Matrix.show(a);
//		System.out.println();
//		Matrix.show(b);
//		System.out.println();
//		Matrix.show(c);}
}

FFT类

主要定义FFT递归版，以及DFT操作，因为我们要求的n必须是2的幂，所以如果给定的向量不满足，则会调用genArray()生成一个满足条件的向量将给定向量末尾补上0。

package fft;public class FFT {/*** 生成w* @param n* @param k* @return*/Complex omega(int n,int k) {return new Complex((Math.cos(2*Math.PI*k/n)),(-Math.sin(2*Math.PI*k/n)));}/*** 找到最小的比n大的2的幂* @param n* @return*/int genN(int n) {int s  =2;while(s<n) {s *=2;}return s;}/*** DFT* @param x* @return*/Complex[][] DFT(Complex[][] x) {int n = x.length;Complex[][] M = new Complex[n][n];for (int i=0;i<n;i++) {for (int j=0;j<n;j++) {M[i][j] = omega(n, i*j);}}return Matrix.mMult(M, x);}/*** FFT递归版本* @param x* @return*/Complex[][] FFT_recurrence(Complex[][] x){int n = x.length;if (n<32)return DFT(x);Complex[][] x_even = FFT_recurrence(Matrix.evenMatrix(x)); Complex[][] x_odd = FFT_recurrence(Matrix.oddMatrix(x));Complex[][] factor = new Complex[n][1];for(int i =0;i<n;i++)factor[i][0] = omega(n, i);Complex[][] a1 = Matrix.subMatrix(factor, 0, n/2);Complex[][] a2 = Matrix.subMatrix(factor, n/2, n);Complex[][] a3 = Matrix.lMult(a1, x_odd);Complex[][] a4 = Matrix.lMult(a2, x_odd);Complex[][] a5 = Matrix.mAdd(a3, x_even);Complex[][] a6 = Matrix.mAdd(a4, x_even);Complex[][] ret = Matrix.concatenate(a5, a6);return ret;}public Complex[][] genArray(Complex[][] x,int n) {int m = x.length;Complex[][] X = new Complex[n][1];for(int i =0;i<n;i++) {if(i<m) X[i][0] = x[i][0];elseX[i][0] = new Complex(0,0);}	return X;}}

测试类

package fft;/**用于测试以及展示用法* @author zhangx**/
public class Main {/*** @param args*/public static void main(String[] args) {int n = 1024;FFT fft = new FFT();//随机生成一个列向量，该向量的每一个元素都是随机的复数Complex[][] x = new Complex[n][1];for (int i =0;i<n;i++)x[i][0] = new Complex(Math.random()%10,Math.random()%10);//因为n可能不是2的幂，所以需要额外生成一个比n大的2次幂维度的向量，用于装xComplex[][] X = fft.genArray(x, fft.genN(n));System.out.println("Matrix X:");Matrix.show(X);System.out.println("************************************");//记录消耗时间long s1 = System.currentTimeMillis();X = fft.FFT_recurrence(X);long s2 = System.currentTimeMillis();System.out.println("Matrix X after FFT:");Matrix.show(X);System.out.println("FFT递归版本耗时："+(s2-s1)+"毫秒");long s3 = System.currentTimeMillis();fft.DFT(X);long s4 = System.currentTimeMillis();System.out.println("DFT耗时："+(s4-s3)+"毫秒");}}

测试结果

python

运行代码

if __name__ == '__main__':#随机生成 维度为1024的列向量x = np.random.random(1024)print('x矩阵为:')print(x)print('fft结果为：')print(fft_recurrence(x))print('')#打印不同方法的fft耗时对比start_1 = time.perf_counter()fft_recurrence(x)end_1 = time.perf_counter()print("fft_recurrence cost：",(end_1-start_1)*1000,'毫秒')start_2 = time.perf_counter()np.fft.fft(x)end_2 = time.perf_counter()print('numpy.fft.fft() cost:', (end_2 - start_2)*1000,'毫秒')start_3 = time.perf_counter()DFT(x)end_3 = time.perf_counter()print('dft cost:', (end_3 - start_3)*1000,'毫秒')# 用numpy.fft的结果和我的fft对比，返回True则两者相同result = np.allclose(fft_recurrence(x),np.fft.fft(x))print('my fft numpy.fft计算出的结果相同？',result)

OUTPUT

我们调用了numpy.fft用于验证我们的FFT是否正确，可以看到python实现的FFT得到的结果是正确的。
现在我们对代码进行一点修改来测验java的FFT是否正确。
替换了x向量为

    x = []for i in range(16):x.append(i)

打印结果为

Java

同样生成16维的向量，[0,1,2…15]

		int n = 16;FFT fft = new FFT();//随机生成一个列向量，该向量的每一个元素都是随机的复数Complex[][] x = new Complex[n][1];for (int i =0;i<n;i++)
//			x[i][0] = new Complex(Math.random()%10,Math.random()%10);x[i][0] = new Complex(i,0);

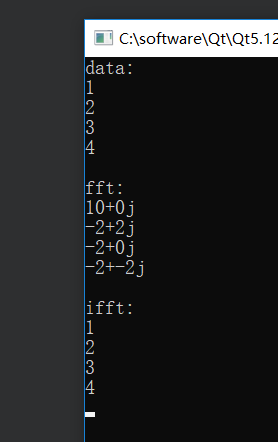
OUTPUT

这里显示0毫秒是因为取的时间是long，长整型，而花费时间小于1毫秒所以显示为0

对比

我们不妨让python版和Java版同时计算一个大向量来看看结果。
现在我们将n变为1024，

java耗时

python耗时

可以看到同样的递归版本，Java耗时比python要少了一半多。这还是在没有进行优化的情况下。