SIR传播模型的科普和预测

article/2025/9/26 8:27:48

>关注公众号：大数据技术派，回复`资料`，领取`1024G`资料。

注：本文仅是个人对于几个疾病模型做的一些概念性描述（科普），并进行了简单的编程实现。切勿当做现实的行动指导。因为文章内容原因，必然会引入现实中的数据，但模型结果与个人倾向无任何关系，本人对结果不持任何立场。

1. 物理模型与机器学习模型

在尝试分析数据的过程中通常会有两种常见的思路： - 物理建模方法 - 机器学习方法

有人说这两种方法是相辅相成的，研究过程的确如此。机器学习方法是在数据量较多，物理机制不明确的情况下的一种妥协之举。举个例子来说：有机器学习专家（专家说法存疑）说使用机器学习方法预测天气，那么天气学家该下岗。这话有两个前提：第一是天气历史数据累积较多；第二做全球范围的天气模拟属于流体力学问题，边界条件复杂，物理模拟困难。现在为止天气预报实际上依然是基于物理建模的，因为其可解释。可解释性对很多问题来说是至关重要的。比如为何会形成飓风，这是物理问题就应该使用物理方式建模。 提到的疾病传播问题，实际上我们很难获取较多训练数据，此时第一个机器学习所需的数据基础便不存在。第二我们更关心疾病是如何传播的，并且如何进行有效的控制。这是模型的可解释性的问题。从这两个维度来看，使用物理模型可能更加合适。

2. SIR模型模拟

2.1 模型描述

SIR模型是属于疾病的动力学模型的一种，属于物理模型（从另一个角度来看也是经验性的总结）。下面来看下这个模型的构建过程。 在描述问题之前先定义几个参数：

  •  当前环境总人口数；

  • 易感染人数  ;

  • 感染人数  ;

  • 恢复人数  。易感染者指的是尚未患病但缺乏免疫力与感染者接触容易受到感染的人群。感染者指的是已经受到疾病感染的人群，并且可以传播给易感染者。恢复者指的是死亡或因为病愈而具有免疫力的人。其中  。

  • 在单位时间内，每个感染者感染的人数与易感染者成正比。比例系数为  为感染强度，单位时间感染者感染人数为  ;

  • 在单位时间内，恢复人数与感染者成正比，比例为  为恢复强度。因此单位时间恢复人数为  。

由此构建微分方程组：

  • 易感人变化：

  • 感染人变化：

  • 恢复人变化： 

2.2 线性微分方程求解

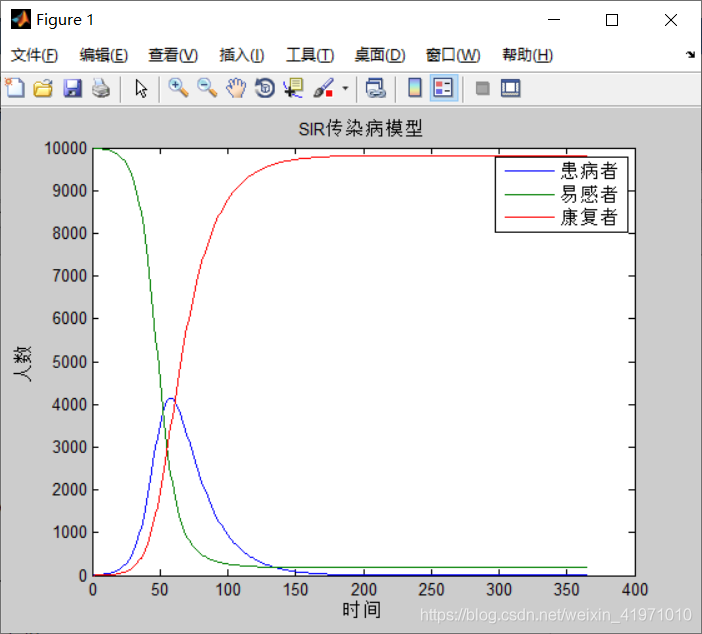
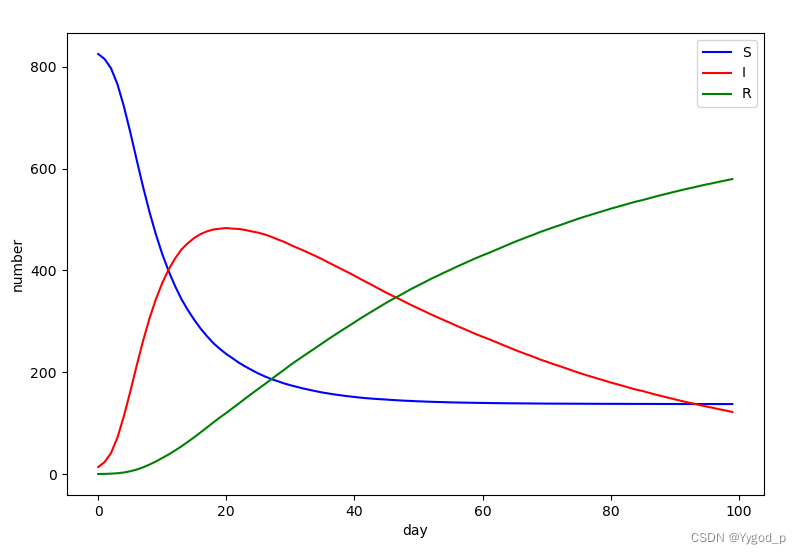
使用有限差分方法求解，在 Python 中的 SciPy 中有求解所需的函数 odeint。 使用的初始值为：易感染人数  人，感染人  ，恢复人  ，感染强度  ，恢复强度  。 得出的结果如图

求解程序为：

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
def SIR(sir, t, beta, gamma):"SIR模型的微分方程"S, I, R = sirdsdt = - beta * S * Ididt = beta * S * I - gamma * Idrdt = gamma * Ireturn [dsdt, didt, drdt]
# 定义时间
t = np.linspace(0, 20, 5000)
# 定义初始情况，易感染人数1000人，感染人1，恢复人0
S0, I0, R0 = 1000, 1, 0
# 感染比例与恢复比分别为
beta, gamma = 0.004, 0.25
# 求解时序变化
result = odeint(SIR, [S0, I0, R0], t, args=(beta, gamma))
St, It, Rt = result[:, 0], result[:, 1], result[:, 2]
# 绘图
plt.plot(t, St, c="g", label="易感染人数变化")
plt.plot(t, It, c="r", label="感染人数变化")
plt.plot(t, Rt, c="b", label="恢复人数变化")
plt.title("SIR模型", fontsize=18)
plt.xlabel("天数", fontsize=18)
plt.ylabel("人数", fontsize=18)
plt.legend(fontsize=18)
plt.grid(True)
plt.show()

2.3 使用SIR模型不负责任的预测

预测问题实际上是预测参数 $\beta, \gamma$。两个参数是可求导的。但是这里使用无需求导的粒子群优化算法（Mathmatica过期了，手算能力又堪忧，所以使用的懒人算法）进行参数估计。这里使用人民日报的数据

以1月24日的为初始值进行曲线拟合。易感染人数设置为10万。并迭代优化

# coding: utf-8
import numpy as np
import random
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# 人群感染数据
data = np.array([23214, 17205, 14380, 11791, 9692,7711, 5974, 4515, 2744, 1975, 1287])[::-1]
# 定义初始情况，易感染人数1000万人，感染人1，恢复人0
S0, I0, R0 = 100000, 1287, 0
# 定义11天
t = np.linspace(0, 10, 11)
def SIR(sir, t, beta, gamma):"SIR模型的微分方程"S, I, R = sirdsdt = - beta * S * Ididt = beta * S * I - gamma * Idrdt = gamma * Ireturn [dsdt, didt, drdt]def f(beta, gamma):# 求解时序变化corr = []for a, b in zip(beta, gamma):result = odeint(SIR, [S0, I0, R0], t, args=(a, b))St, It, Rt = result[:, 0], result[:, 1], result[:, 2]corr.append(np.mean((It-data)**2))return np.array(corr)
# 定义粒子个数
N = 20
# 定义惯性因子
w = 0.1
# 定义C1，C2
c1, c2 = 2, 2
# 初始化位置
x = np.random.uniform(0, 1, [N, 2])
x[:, 0] *= 0.04
x[:, 1] *= 0.25
# 初始化速度
v = np.random.uniform(0, 1, [N, 2])
v[:, 0] *= 0.04 * 0.03
v[:, 1] *= 0.25 * 0.03
# 个体最佳位置
p_best = np.copy(x)fitness = f(x[:, 0], x[:, 1])
fitness = np.expand_dims(fitness, 1)
# 群体最佳位置
g_best = p_best[np.argmin(fitness)]
N_step = 100
store = np.zeros([N, N_step, 2])
for step in range(N_step):# 计算速度vstore[:, step, :] = xr1, r2 = np.random.random([N, 1]), np.random.random([N, 1])v = w * v + (1-w)*(c1 * r1 * (p_best - x) + c2 * r2 * (g_best - x))# 更新位置x = x + vx = np.clip(x, 0, 0.5)# 计算适应度fitness_new = f(x[:, 0], x[:, 1])fitness_new = np.expand_dims(fitness_new, 1)fit = np.concatenate([fitness, fitness_new], 1)fitness = fitness_new# 计算个体最优解p_best_for_sel = np.concatenate([np.expand_dims(x, 1),np.expand_dims(p_best, 1)], 1)p_best = p_best_for_sel[[i for i in range(N)], np.argmin(fit, 1), :]fit_p = f(p_best[:, 0], p_best[:, 1])# 计算全局最优解g_best = x[np.argmin(fitness[:, 0])]print(g_best)
a, b = g_best
dt = np.linspace(0, 30, 1000)
result = odeint(SIR, [S0, I0, R0], dt, args=(a, b))
St, It, Rt = result[:, 0], result[:, 1], result[:, 2]# 绘图
fig, ax1 = plt.subplots()
ax1.plot(t, data, c="g", label="真实感染人数")
ax1.plot(dt, It, c="r", linestyle="--", label="预测感染人数")ax2 = ax1.twinx()
ax2.plot(dt[1:], It[1:]-It[:-1], c="b", label="增长人数")
ax2.legend()
ax2.set_ylabel("增长人数", fontsize=18)
ax1.set_title("SIR模型拟合", fontsize=18)
ax1.set_xlabel("天数", fontsize=18)ax1.set_ylabel("人数", fontsize=18)
ax1.legend(fontsize=18)
plt.grid(True)
time = np.linspace(0, 30, 31)
name = [f"1-{itr}" for itr in range(24, 32)]+[f"2-{itr}" for itr in range(1, 23)]
plt.xticks(time, name)
plt.show()

最终得到的结果如图所示

可以看到，大概在2月6日或7日达到峰值。也就是快结束了。 当然这个模型并不准确，初始值选择、实际模型契合度、易感染人群数都是不确定的，同时易感染人数也应当是可训练的，这里仅作拟合使用，其他读者可以自行填写代码进行修改。

3. 其他模型

在疾病传播的模型中还有其他模型可以使用比如 SEIR 模型等，这些模型与 SIR 模型大同小异，仅添加了多个求解函数而已。从另外一个角度来看这些模型，当前状态可以完全决定未来数据趋势，因此是一个马尔科夫过程。这类模型问题在于仅是一个统计特征（有点像机器学习）。无法复现现代社会传播的复杂性。现代社会是一个复杂的关系网络，如图 Twitter 关网络：

在这个关系网络上的 SIR 模型更加符合社会规律：

比如武汉作为交通枢纽连接了多个城市交通中心，而这个交通中心又向各个县城等节点输送感染者。这使得感染模型映射于一个巨大的社会网络上。使用这个模型可以更加细致的进行传播分析。 然而最终模拟的结果可能表现出与 SIR 模型相近的统计特征。这似乎又回到了原点，但这个过程中却了解了疾病传播的根本原理。这才是科学研究的过程，此个过程中机器学习方法可作为辅助。

4. 总结

第三部分写的简略了一些，因为程序尚未编写完成。当然也不一定有时间去完成，因为写这些东西仅仅是兴趣，本身研究方向并不在此。 本文目的仅仅是对于疾病传播模型的一点点科普。在行文过程中参考了很多 $CSDN$ 的文章（其实并没有，并且其很讨厌）。 最后任何困难都会过去的。

参考文献

  1. 徐宝春. 基于SIR模型的SARS传染病研究[D]. 山东大学

  2. Vespignani, Alessandro. Modelling dynamical processes in complex socio-technical systems[J]. Nature Physics, 2011, 8(1):32-39.

  3. Tolić D, Kleineberg K K, Antulov-Fantulin N. Simulating SIR processes on networks using weighted shortest paths[J]. Scientific reports, 2018, 8(1): 1-10.

  4. 其他乱起八糟的科普文章。

知乎原文链接

https://zhuanlan.zhihu.com/p/105027022?utm_source=wechat_session

猜你喜欢

  • 贝叶斯定理的通俗理解

  • 用户画像构建（理论篇）

  • 常见的几种最优化方法

  • 微信抢红包背后的数学算法


http://chatgpt.dhexx.cn/article/gchEeBt5.shtml

相关文章

6.复杂网络实验六：SIR病毒传播模型（matlab）

6.复杂网络实验六：SIR病毒传播模型（matlab）

一、SIR模型简介 在典型的传染病模型中，种群（Population）内的N个个体的状态可分为如下几类： (1)、易染状态S(Susceptible),即健康状态，可被感染的个体。 (2)、感染状态I(Infected),处于感染状态的个体还能够感染将康…
阅读更多...
传染病SIR传播模型（搬运，含带MATLAB代码）

传染病SIR传播模型（搬运，含带MATLAB代码）

学习笔记之SIR传染病模型TOC 本文主要是对此篇文章代码部分的详解 function ysir(~,x)a0.8; %感染率0.8b0.2; %治愈率0.2y[-a*x(1)*x(2),a*x(1)*x(2)-b*x(2),b*x(2)]; end %t 为持续时间，%x为三维矩阵，其中x(1)为易感染者，x(2)为传染者&…
阅读更多...
传染病模型（4）——SIRS模型和SIER模型及matlab具体程序

传染病模型（4）——SIRS模型和SIER模型及matlab具体程序

前言 常见的传染病模型按照具体的传染病的特点可分为 SI、SIS、SIR、SIRS、SEIR 模型。其中“S”“E”“I”“R”的现实含义如下： S (Susceptible)，易感者，指缺乏免疫能力健康人，与感染者接触后容易受到感染； E (Ex…
阅读更多...
信息传播模型——SIR的Python实现

信息传播模型——SIR的Python实现

本文通过Python语言实现SIR模型，并进行可视化，所用例子为足球俱乐部数据集。 author：xiao黄 缓慢而坚定的生长 我之前还写过SI和IC模型的Python实现及可视化，请点击传送门查看，希望对你们有帮助。 SIR模型是传染病模型…
阅读更多...
疫情模拟中的SIR模型与扩展的SIRD模型

疫情模拟中的SIR模型与扩展的SIRD模型

一.SIR模型 SIR模型起源于流行病学的研究，是模拟传染病动力学的经典模型。至今仍在流行病学中占据中心位置，核心在于微分方程。 SIR模型描述了流行病下三大人群：易感者 susceptible、感染者 infectious、痊愈者 recovered之间的关系。 SIR模…
阅读更多...
基于SIR模型的疫情预测 matlab

基于SIR模型的疫情预测 matlab

基于SIR模型的疫情预测 庚子年 庚辰月 丁丑日，疫情从爆发到今天，已经有100多万人感染，而我国有一群这样的逆行者他们以自己的生命筑起了我国的防疫长城，鲁迅先生曾说“我们从古以来，就有埋头苦干的人，有拼…
阅读更多...
python实现SI、SIS、SIR、SIRS、SEIR、SEIRS模型

python实现SI、SIS、SIR、SIRS、SEIR、SEIRS模型

传染病传播模型 SISISSIRSIRSSEIR（相比较贴合新冠状病毒）SEIRS 在家闲着无事，搜了一些关于传染病模型的知识，在此做个总结。 SI 最简单的SI模型首先把人群分为2种，一种是易感者(Susceptibles)，易感者是健康…
阅读更多...
流行病模型(SIR Model)

流行病模型(SIR Model)

流行病模型(SIR Model) by : ZhuoFei, Zhou 首先定义一个函数bernoulli(p) #以概率p判断是否会被感染或恢复 function bernoulli(p::Number)if rand(1)[1] < preturn trueelsereturn falseend endbernoulli (generic function with 1 method)恢复所需的时间函数recovery_…
阅读更多...
SIR模型与R模拟

SIR模型与R模拟

SIR病毒模型R模拟 文章目录 SIR病毒模型R模拟[toc]1.SIR病毒模型2.R模拟 1.SIR病毒模型 SIR病毒模型的的三个字母分别为病毒传播过程中的三种状态&#xff0c;其中 S&#xff0c;表示易感染者&#xff0c;即没有被感染病毒的人群I&#xff0c;表示已感染者&#xff0c;即被感…
阅读更多...
【python】SIR模型实现

【python】SIR模型实现

SIR模型python实现 SIR模型是传染病模型中最经典的模型&#xff0c;其中S表示易感者&#xff0c;I表示感染者&#xff0c;R表示恢复者。SIR模型中&#xff0c;染病人群为传染的源头,他通过一定的几率把传染病传给易感人群,他自己也有一定的几率/可以被治愈并免疫,或者死亡;易感…
阅读更多...
传染病模型（3）——SIR模型及matlab运行结果

传染病模型（3）——SIR模型及matlab运行结果

前言 常见的传染病模型按照具体的传染病的特点可分为 SI、SIS、SIR、SIRS、SEIR 模型。其中“S”“E”“I”“R”的现实含义如下&#xff1a; S (Susceptible)&#xff0c;易感者&#xff0c;指缺乏免疫能力健康人&#xff0c;与感染者接触后容易受到感染&#xff1b; E (Exp…
阅读更多...
关于SIR模型性质的进一步摘录

关于SIR模型性质的进一步摘录

1 SIR模型的性质 又是成为SIR搬运工的一天。以下内容来自陈卫老师在《大数据网络传播模型和算法》。纯纯自我记录&#xff0c;不够美观不够细致&#xff0c;不喜欢看出门左拐。 1.1 SIR模型中的basic reproduction rate&#xff08;基础再生数&#xff09; R 0 R_0 R0​ 它是…
阅读更多...
SIR模型II

SIR模型II

SIR II (Epidemic modeling) by Zhuofei(fregoticloud.com) jupyter notebook link 在这个模型中&#xff0c;考虑一个在一定空间内的流行病模型。人只能与附近的人交互作用&#xff0c;所以给人在一定的空间里随机运动。 首先&#xff0c;在一个2维平面&#xff0c;随机游走&…
阅读更多...
SIR信息传播模型

SIR信息传播模型

SIR信息传播模型 SIR模型及python复现SIR模型SIR数学模型传播动力学方程python实现 模拟社交网络中SIR模型的信息传播过程 SIR模型及python复现 SIR模型 SIR模型是传染病模型中的经典模型&#xff0c;可以用在传染病过程中的模拟预测&#xff0c;也可以用作抽象表达社交网络中…
阅读更多...
SIR模型 matlab模拟

SIR模型 matlab模拟

需要一个单独的m文件&#xff1a; %即写上三个微分方程 function ySIRModel(t,x,lambda,mu) y[-lambda*x(1)*x(2),lambda*x(1)*x(2)-mu*x(2),mu*x(2)]; 再进行作图 >> ts0:1:100; >> lambda0.00001; >> mu1/14; >> x0[45400,2100,2500]; >> […
阅读更多...
SIR及SEIR建模的简单示例

SIR及SEIR建模的简单示例

目录 概述1.一些定义1.1 一些名词1.2 一些符号1.3 一些定义 2.方法论2.1 SIR2.2 SEIR2.3 代际传播2.3.1 传播矩阵 3 模型实现3.1 参数设定3.2 SIR&#xff08;1&#xff09;模型&#xff08;2&#xff09;参数&#xff08;3&#xff09;计算&#xff08;4&#xff09;绘图 3.3 …
阅读更多...
SIR模型python实现

SIR模型python实现

python新手&#xff0c;代码不规范之处敬请见谅&#xff0c;第一次发帖排版也不太懂&#xff0c;各位将就看。 参考&#xff1a; SIR模型和Python实现_阿丢是丢心心的博客-CSDN博客_sir模型 【保姆级教程】使用python实现SIR模型&#xff08;包含数据集的制作与导入及最终结…
阅读更多...
SI，SIS，SIR，SEIRD模型

SI，SIS，SIR，SEIRD模型

SI&#xff0c;SIS&#xff0c;SIR&#xff0c;SEIRD模型 因为个人工作需要系统地整理SI&#xff0c;SIR以及SEIR模型&#xff0c;故对三个模型进行原理介绍以及对比。文中关于SI&#xff0c;SIS&#xff0c;SIR的所有的截图都来自西工大肖华勇老师在慕课上的分享&#xff0c;…
阅读更多...
【数学建模】传染病SIR模型

【数学建模】传染病SIR模型

SIR模型 经典的SIR模型是一种发明于上个世纪早期的经典传染病模型&#xff0c;此模型能够较为粗略地展示出一种传染病的发病到结束的过程&#xff0c;其核心在于微分方程&#xff0c;其中三个主要量S是易感人群&#xff0c;I是感染人群&#xff0c;R是恢复人群 这三个量都是跟…
阅读更多...
SIR模型简单了解（Susceptible Infected Recovered Model）

SIR模型简单了解（Susceptible Infected Recovered Model）

SIR模型定义 SIR模型是一种传播模型&#xff0c;是信息传播过程的抽象描述。 SIR模型是传染病模型中最经典的模型&#xff0c;其中S表示易感者&#xff0c;I表示感染者&#xff0c;R表示移除者。 S&#xff1a;Susceptible&#xff0c;易感者 I&#xff1a;Infective&#xf…
阅读更多...
推荐文章

Copyright @ 2022~2023