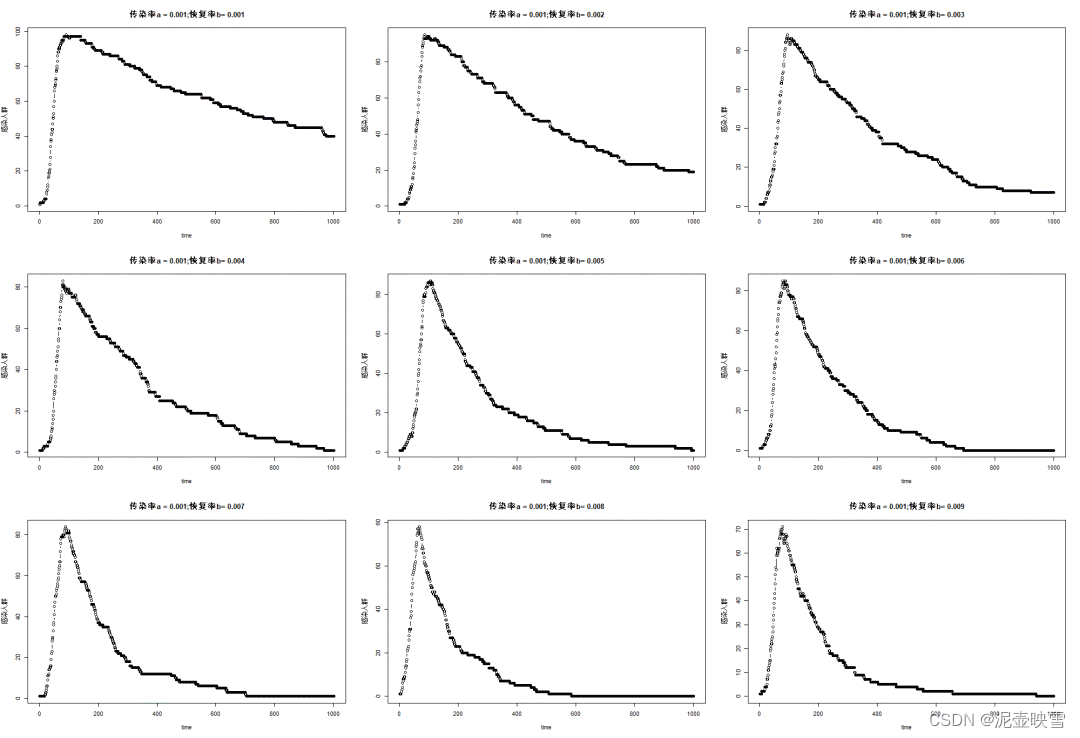
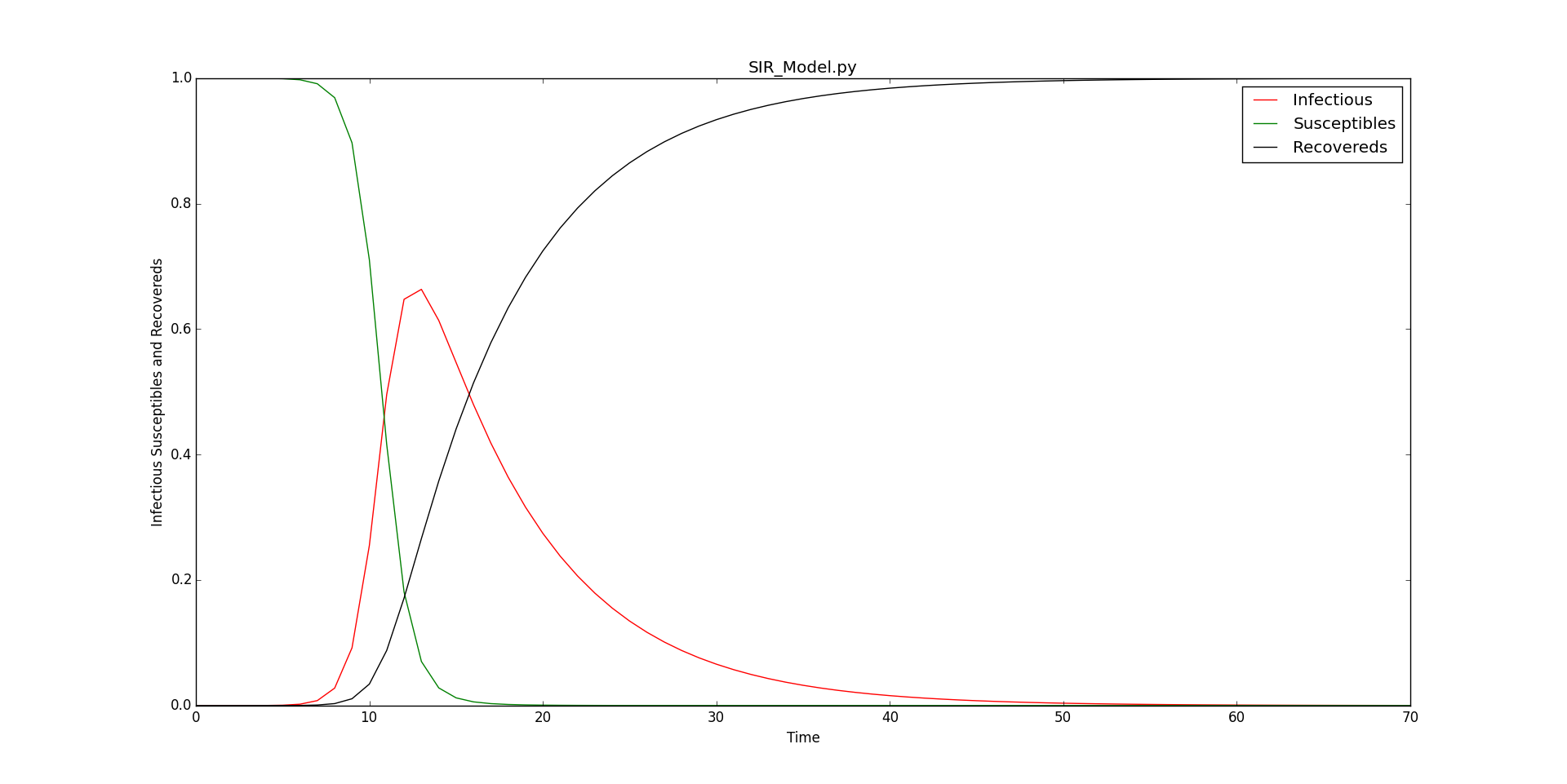
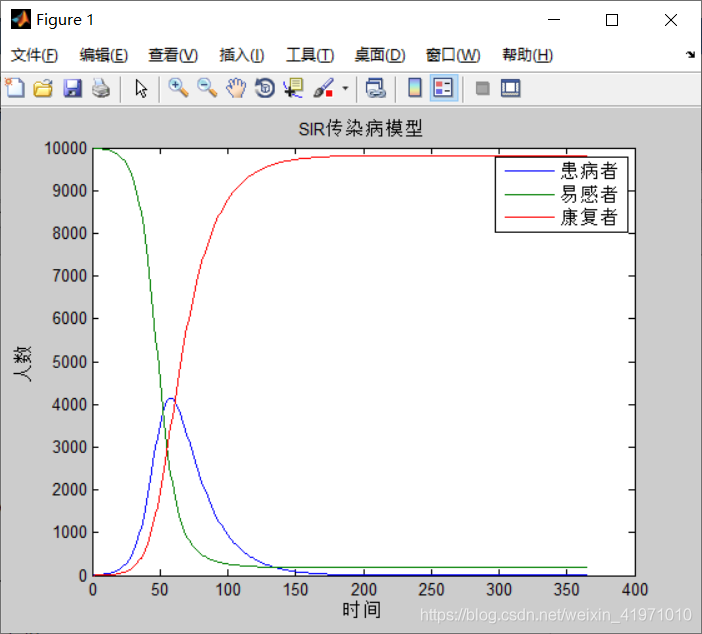
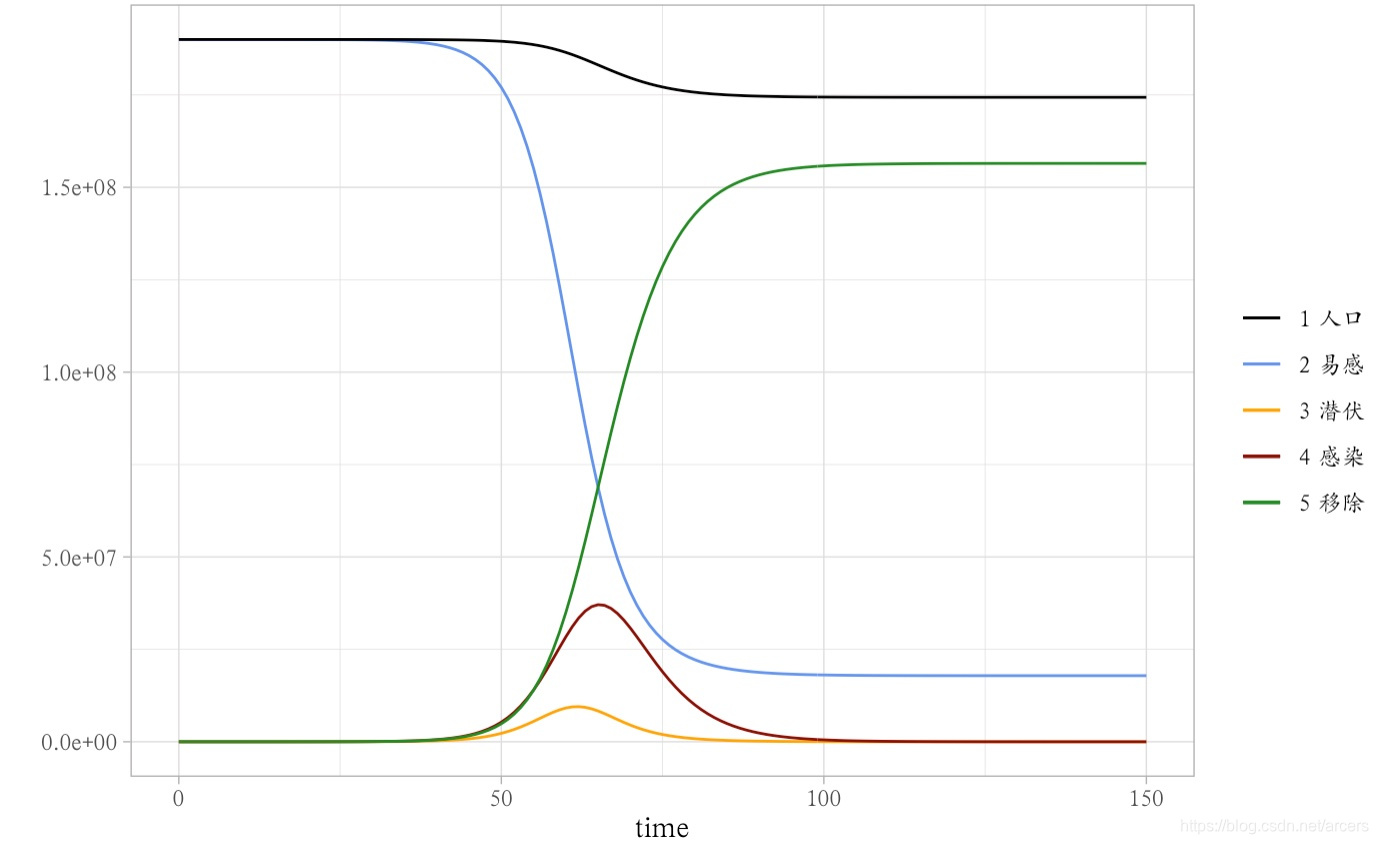
传染病传播模型
- SI
- SIS
- SIR
- SIRS
- SEIR(相比较贴合新冠状病毒)
- SEIRS
在家闲着无事,搜了一些关于传染病模型的知识,在此做个总结。
SI
最简单的SI模型首先把人群分为2种,一种是易感者(Susceptibles),易感者是健康的人群,用S表示其人数,另外一种是感染者(The Infected),人数用 I来表示。
假设:
1、在疾病传播期间总人数N不变,N=S+I
2、每个病人每天接触人数为定值
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0
# I_0为感染者的初始人数
I_0 = 1
# S_0为易感者的初始人数
S_0 = N - I_0
# 感染者每天接触人数
P = 1
# T为传播时间
T = 150# INI为初始状态下的数组
INI = (S_0,I_0)def funcSI(inivalue,_):Y = np.zeros(2)X = inivalue# 易感个体变化Y[0] = - (P * beta * X[0] * X[1]) / N + gamma * X[1]# 感染个体变化Y[1] = (P * beta * X[0] * X[1]) / N - gamma * X[1]return YT_range = np.arange(0,T + 1)RES = spi.odeint(funcSI,INI,T_range)plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.')
plt.title('SI Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()

SIS
在SI模型基础上加入康复的概率
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0.05
# I_0为感染者的初始人数
I_0 = 1
# S_0为易感者的初始人数
S_0 = N - I_0
# T为传播时间
T = 150# INI为初始状态下的数组
INI = (S_0,I_0)def funcSIS(inivalue,_):Y = np.zeros(2)X = inivalue# 易感个体变化Y[0] = - (beta * X[0]) / N * X[1] + gamma * X[1]# 感染个体变化Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]return YT_range = np.arange(0,T + 1)RES = spi.odeint(funcSIS,INI,T_range)plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.')
plt.title('SIS Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()

SIR
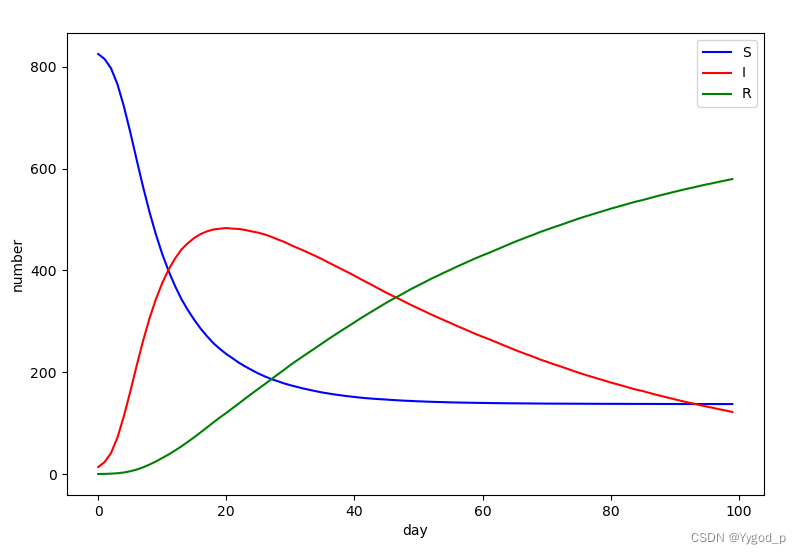
SIR是三个单词首字母的缩写,其中S是Susceptible的缩写,表示易感者;I是Infective的缩写,表示感染者;R是Removal的缩写,表示移除者。这个模型本身是在研究这三者的关系。在病毒最开始的时候,所有人都是易感者,也就是所有人都有可能中病毒;当一部分人在接触到病毒以后中病毒了,变成了感染者;感染者会接受各种治疗,最后变成了移除者。
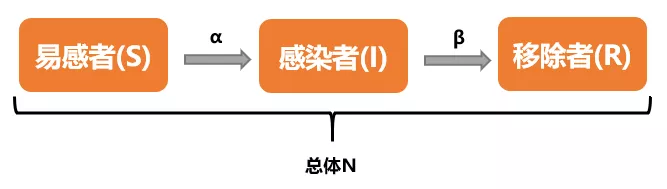
该模型有两个假设条件
1.一段时间内总人数N是不变的,也就是不考虑新生以及自然死亡的人数
2.从S到I的变化速度α、从I到R的变化速度β也是保持不变的
3.移除者不再被感染
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0.05
# I_0为感染者的初始人数
I_0 = 1
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - R_0
# T为传播时间
T = 150# INI为初始状态下的数组
INI = (S_0,I_0,R_0)def funcSIR(inivalue,_):Y = np.zeros(3)X = inivalue# 易感个体变化Y[0] = - (beta * X[0] * X[1]) / N# 感染个体变化Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]# 治愈个体变化Y[2] = gamma * X[1]return YT_range = np.arange(0,T + 1)RES = spi.odeint(funcSIR,INI,T_range)plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.')
plt.plot(RES[:,2],color = 'green',label = 'Recovery',marker = '.')
plt.title('SIR Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()

SIRS
与SIR不同在于,康复者的免疫力是暂时的,康复者会转化为易感者
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0.05
# Ts为抗体持续时间
Ts = 7
# I_0为感染者的初始人数
I_0 = 1
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - R_0
# T为传播时间
T = 150# INI为初始状态下的数组
INI = (S_0,I_0,R_0)def funcSIRS(inivalue,_):Y = np.zeros(3)X = inivalue# 易感个体变化Y[0] = - (beta * X[0] * X[1]) / N + X[2] / Ts# 感染个体变化Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]# 治愈个体变化Y[2] = gamma * X[1] - X[2] / Tsreturn YT_range = np.arange(0,T + 1)RES = spi.odeint(funcSIRS,INI,T_range)plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'red',label = 'Infection',marker = '.')
plt.plot(RES[:,2],color = 'green',label = 'Recovery',marker = '.')
plt.title('SIRS Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()

SEIR(相比较贴合新冠状病毒)
在其他模型的基础上,加入传染病潜伏期的存在,更贴合这次的新冠状病毒
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt# N为人群总数
N = 10000
# β为传染率系数
beta = 0.6
# gamma为恢复率系数
gamma = 0.1
# Te为疾病潜伏期
Te = 14
# I_0为感染者的初始人数
I_0 = 1
# E_0为潜伏者的初始人数
E_0 = 0
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - E_0 - R_0
# T为传播时间
T = 150# INI为初始状态下的数组
INI = (S_0,E_0,I_0,R_0)def funcSEIR(inivalue,_):Y = np.zeros(4)X = inivalue# 易感个体变化Y[0] = - (beta * X[0] * X[2]) / N# 潜伏个体变化(每日有一部分转为感染者)Y[1] = (beta * X[0] * X[2]) / N - X[1] / Te# 感染个体变化Y[2] = X[1] / Te - gamma * X[2]# 治愈个体变化Y[3] = gamma * X[2]return YT_range = np.arange(0,T + 1)RES = spi.odeint(funcSEIR,INI,T_range)plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'orange',label = 'Exposed',marker = '.')
plt.plot(RES[:,2],color = 'red',label = 'Infection',marker = '.')
plt.plot(RES[:,3],color = 'green',label = 'Recovery',marker = '.')plt.title('SEIR Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()

SEIRS
同时有潜伏期且免疫暂时的条件
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt# N为人群总数
N = 10000
# β为传染率系数
beta = 0.6
# gamma为恢复率系数
gamma = 0.1
# Ts为抗体持续时间
Ts = 7
# Te为疾病潜伏期
Te = 14
# I_0为感染者的初始人数
I_0 = 1
# E_0为潜伏者的初始人数
E_0 = 0
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - E_0 - R_0
# T为传播时间
T = 150# INI为初始状态下的数组
INI = (S_0,E_0,I_0,R_0)def funcSEIRS(inivalue,_):Y = np.zeros(4)X = inivalue# 易感个体变化Y[0] = - (beta * X[0] * X[2]) / N + X[3] / Ts# 潜伏个体变化Y[1] = (beta * X[0] * X[2]) / N - X[1] / Te# 感染个体变化Y[2] = X[1] / Te - gamma * X[2]# 治愈个体变化Y[3] = gamma * X[2] - X[3] / Tsreturn YT_range = np.arange(0,T + 1)RES = spi.odeint(funcSEIRS,INI,T_range)plt.plot(RES[:,0],color = 'darkblue',label = 'Susceptible',marker = '.')
plt.plot(RES[:,1],color = 'orange',label = 'Exposed',marker = '.')
plt.plot(RES[:,2],color = 'red',label = 'Infection',marker = '.')
plt.plot(RES[:,3],color = 'green',label = 'Recovery',marker = '.')plt.title('SEIRS Model')
plt.legend()
plt.xlabel('Day')
plt.ylabel('Number')
plt.show()