SIR病毒模型R模拟

文章目录

• SIR病毒模型R模拟
• • @[toc]
  • 1.SIR病毒模型
  • 2.R模拟

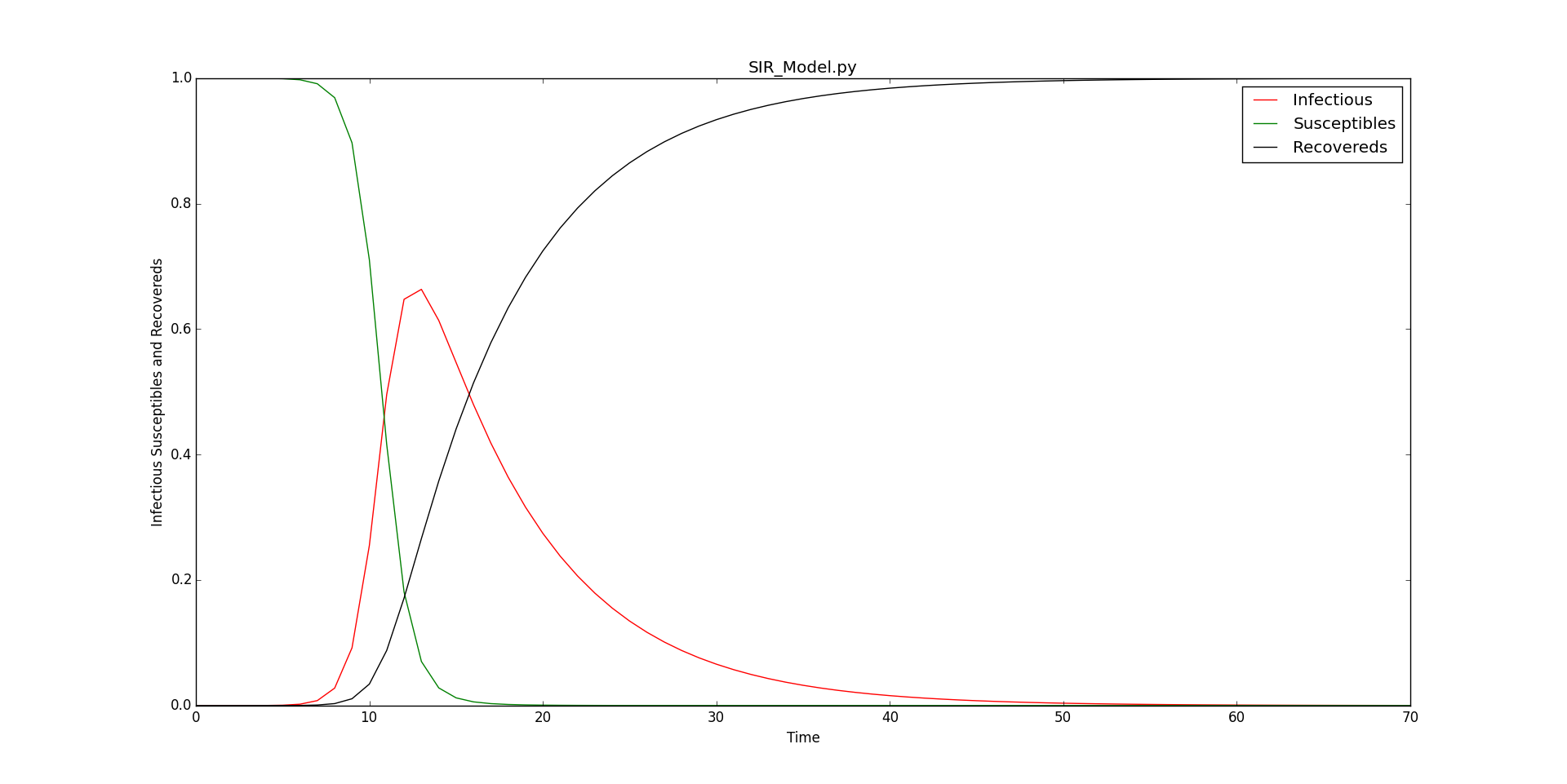
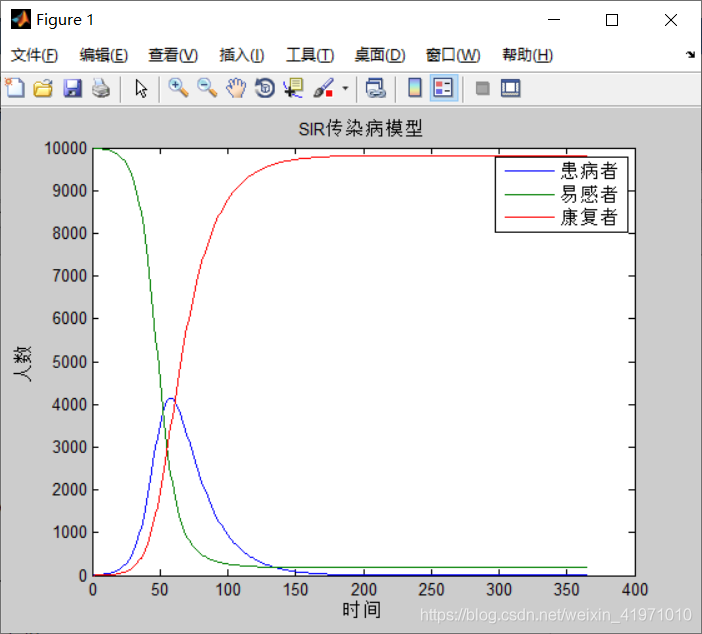
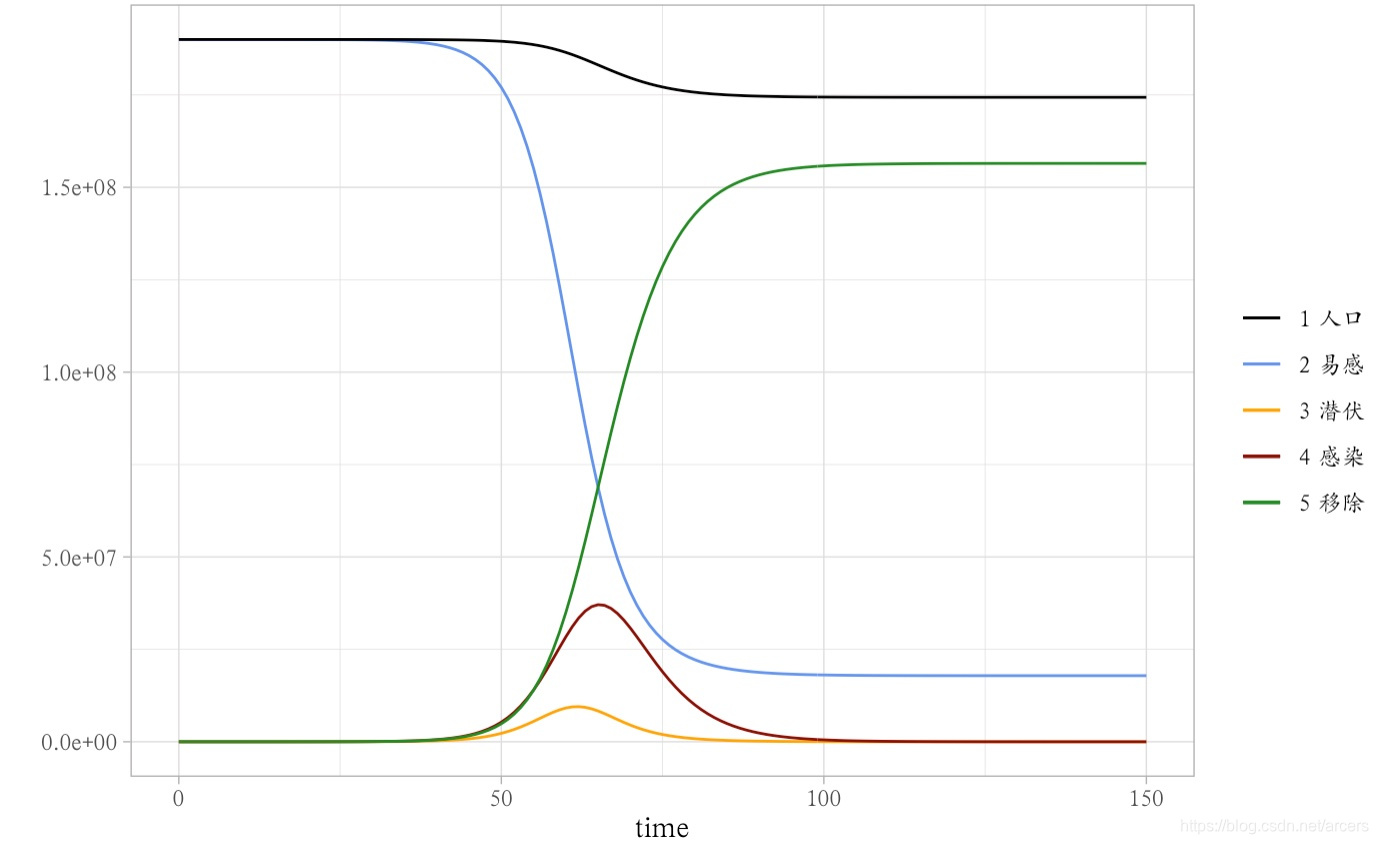
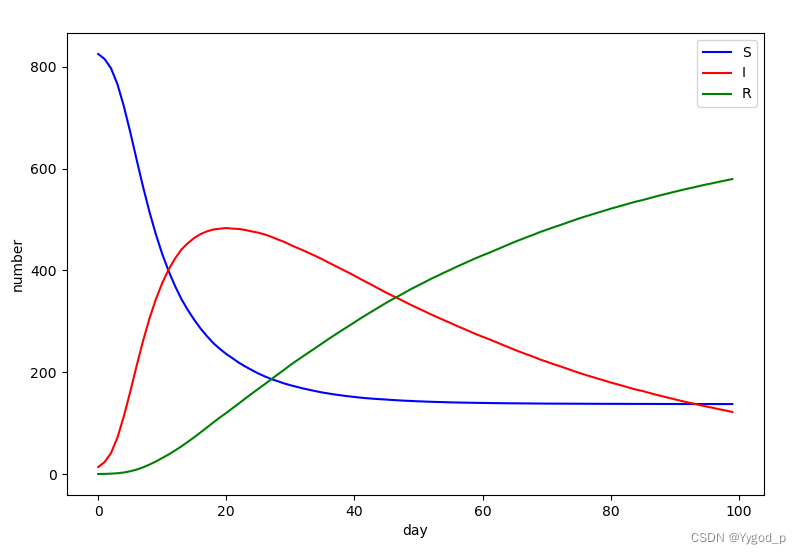
1.SIR病毒模型

SIR病毒模型的的三个字母分别为病毒传播过程中的三种状态，其中

• S，表示易感染者，即没有被感染病毒的人群
• I，表示已感染者，即被感染病毒的人群
• R，表示感染后恢复者，即感染后恢复人群

设总人口为$N+1$,初始感染人群$I(1)=1$,易感染人群$S(1)=N$，恢复人群$R(0)=0$。在任意时刻$t$每个感染者以概率$\alpha$使易感染者染病，感染者以概率$\beta$解除或恢复。在时刻$t$，易感染者未被感染的概率为$(1-\alpha {)}^{I(t)}$ 于是得到递归公式
$$\{\begin{array}{l}S(t)+I(t)+R(t)=N+1\\ S(t+1)\sim binom(S(t),(1-\alpha {)}^{I(t)})\\ R(t+1)\sim R(t)+binom(I(t),\beta )\\ I(t+1)\sim N+1-S(t+1)-R(t+1)\\ S(1)=N;R(0)=0;I(1)=1\end{array}$$

---

2.R模拟

下面是R模拟代码

#------------SIR病毒模型模拟-----------------
# SIR函数定义
SIR <- function(a,b,N,T){# SIR病毒扩散模型# 参数a为感染率# 参数b为移除率# N人口总数# t考察时间S <- rep(0,T+1) # 易感染着I <- rep(0,T+1) # 感染者R <- rep(0,T+1) # 移除者S[1] <- NI[1] <- 1R[1] <- 0for(i in 1:T){S[i+1] <- rbinom(1,S[i],(1-a)^I[i]) R[i+1] <- R[i] + rbinom(1,I[i],b)I[i+1] <- N + 1 - R[i+1] - S[i+1]}return(matrix(c(S,I,R),ncol = 3))
}# 比较静态模拟
T = 1000 # 考察时间1000(天)
a = 0.001 # 感染率
N = 100 # 人口总数
par(mfrow = c(3,3))
L <- c(0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9)/100
for(b in L){M <- SIR(a,b,N,T)time <- seq(1,nrow(M),1)plot(time,M[,2],ylab = "I",type = "b",main = paste("传染率a = 0.001;恢复率b=",b)) # 感染人群
}

输出结果

---

-END-