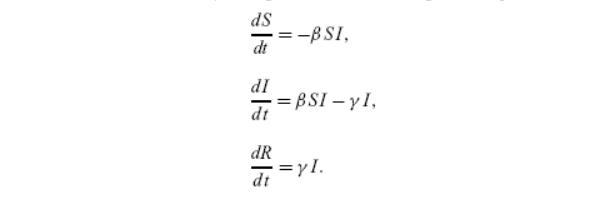SIR模型python实现
SIR模型是传染病模型中最经典的模型,其中S表示易感者,I表示感染者,R表示恢复者。SIR模型中,染病人群为传染的源头,他通过一定的几率把传染病传给易感人群,他自己也有一定的几率/可以被治愈并免疫,或者死亡;易感人群一旦被感染,就又成为了新的传染源。将人群划分为三类,易感染者、已感染者和已恢复者(recovered )。
可建立下面的三房室模型:
其中:
Parameters
| β | is the transmission rate and incorporates the encounter rate between susceptible and infectious individuals together with the probability of transmission. |
| γ | is called the removal or recovery rate, though often we are more interested in its reciprocal (1/γ) which determines the average infectious period. |
| S(0) | is the initial proportion of the population that are susceptible. |
| I(0) | is the initial proportion of the population that are infectious. |
pythonCode:
import scipy.integrate as spi
import numpy as np
import pylab as plbeta=1.4247
gamma=0.14286
TS=1.0
ND=70.0
S0=1-1e-6
I0=1e-6
INPUT = (S0, I0, 0.0)def diff_eqs(INP,t):'''The main set of equations'''Y=np.zeros((3))V = INPY[0] = - beta * V[0] * V[1]Y[1] = beta * V[0] * V[1] - gamma * V[1]Y[2] = gamma * V[1]return Y # For odeintt_start = 0.0; t_end = ND; t_inc = TS
t_range = np.arange(t_start, t_end+t_inc, t_inc)
RES = spi.odeint(diff_eqs,INPUT,t_range)print RES#Ploting
pl.subplot(111)
pl.plot(RES[:,1], '-r', label='Infectious')
pl.plot(RES[:,0], '-g', label='Susceptibles')
pl.plot(RES[:,2], '-k', label='Recovereds')
pl.legend(loc=0)
pl.title('SIR_Model.py')
pl.xlabel('Time')
pl.ylabel('Infectious Susceptibles and Recovereds')
pl.xlabel('Time')
pl.show()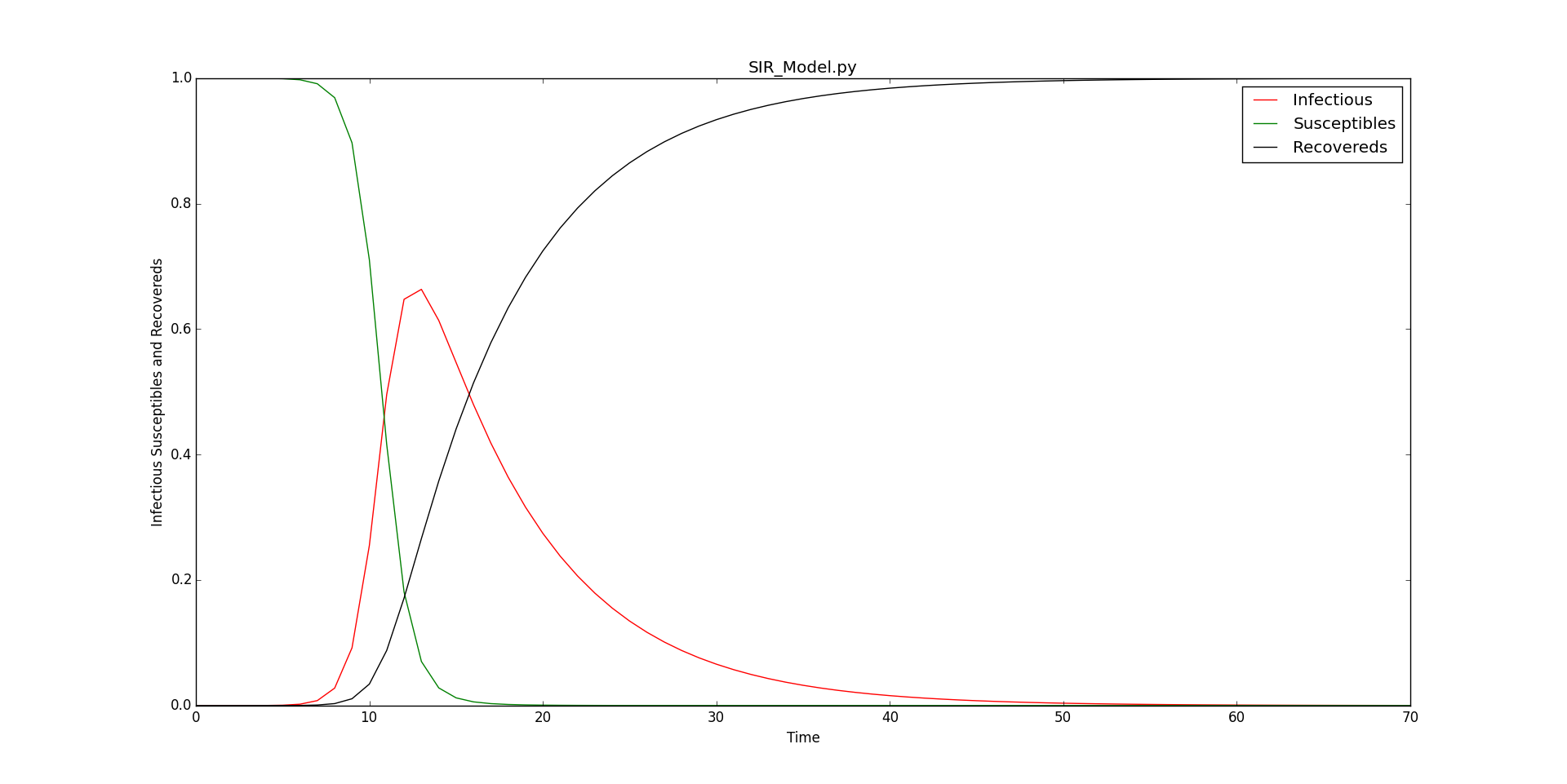
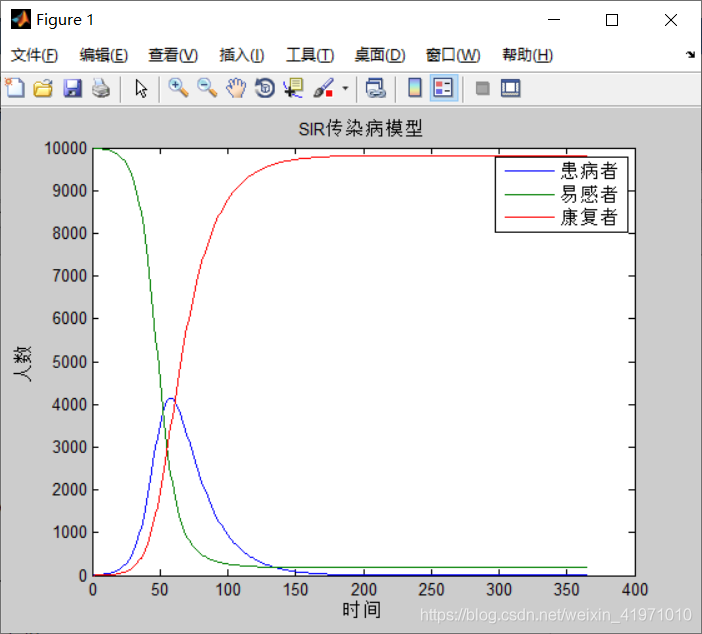
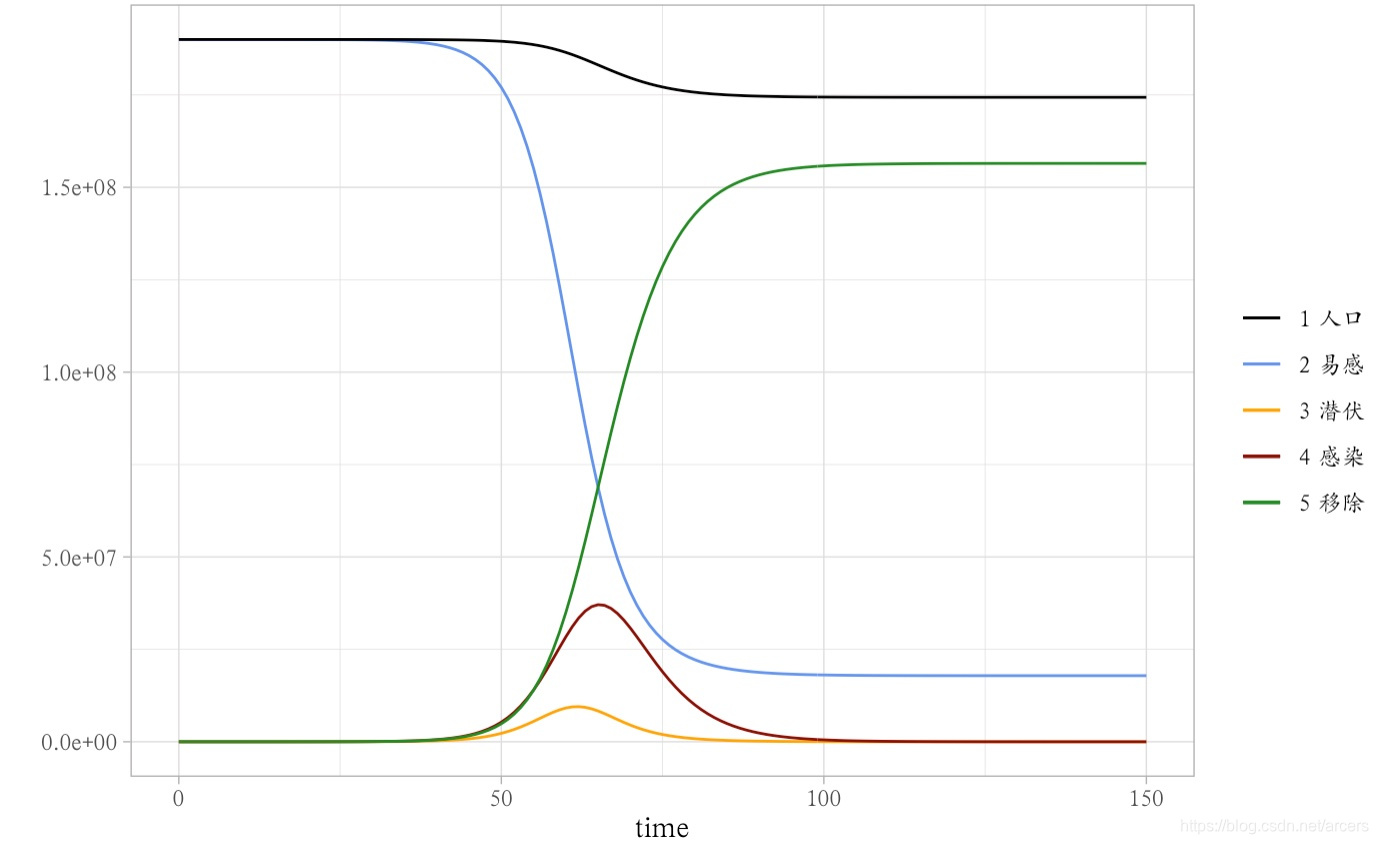
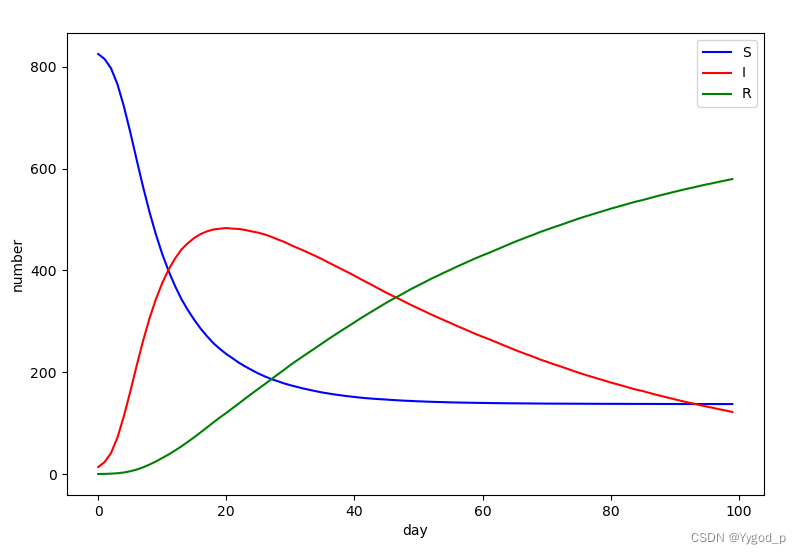
从图中可见,随着时间的推移传播者刚开始急速上升再缓慢下降。恢复者持续上升趋于稳定,易感染者持续下降趋于稳定。该模型是SIR中最基本模型,此外还有一些考虑出生率、死亡率等因素的模型变种。
参考链接:
SIR模型参考