基于SIR模型的疫情预测

庚子年庚辰月丁丑日，疫情从爆发到今天，已经有100多万人感染，而我国有一群这样的逆行者他们以自己的生命筑起了我国的防疫长城，鲁迅先生曾说“我们从古以来，就有埋头苦干的人，有拼命硬干的人，有为民请命的人，有舍身求法的人，……虽是等于为帝王将相作家谱的所谓"正史"，也往往掩不住他们的光耀，这就是中国的脊梁。”
愿逝者安息，山河无恙。

尘沉尘的第一篇博客

这是前一段时间，数学建模课的一道作业，一直想写一篇博客，但是想想真的拖了好久。

、

SIR
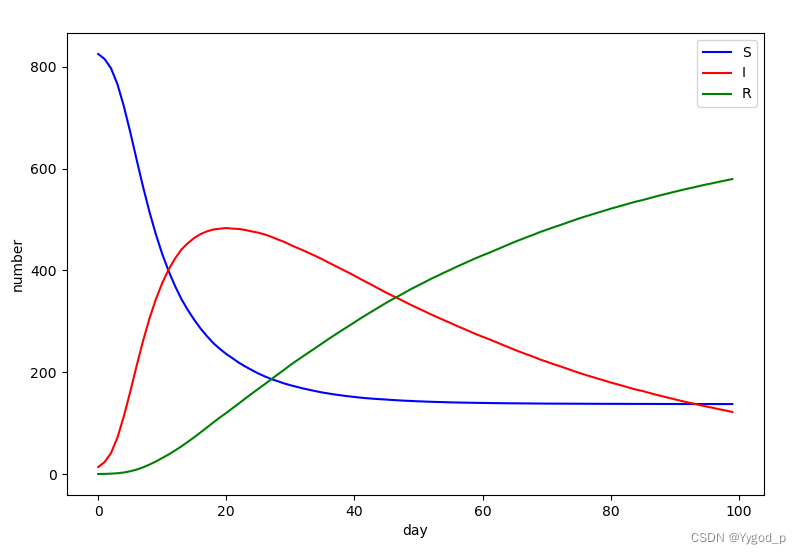
SIR模型是是一种传播模型，是信息传播过程的抽象描述。是传染病模型中最经典的模型，其中S表示易感者，I表示感染者，R表示移出者。

历史

传染病模型有着悠久的历史，一般认为始于1760年Daniel Bernoulli在他的一篇论文中对接种预防天花的研究。1927年Kermack与McKendrick在研究流行于伦敦的黑死病时提出了的SIR仓室模型，并于1932年继而建立了SIS模型，在对这些模型的研究基础上提出了传染病动力学中的阈值理论。

SIR模型的建立

基本假设
(1) 假设给定数据真实，不考虑人口的出生、死亡、流动等，该城市人口总数N是常数，即每年流入人口等于流出人口
(2) 假设人口当日所处的健康状态只分为健康人群、感染新型冠状病毒确诊病人和恢复者三类类;
(3) 假设人口不可流动，即无病人流入和流出该城市;
(4) 假设严格隔离的新型冠状病毒感染病人都不再传染他人;
符号说明
N——我们所研究区域的人口总数；
S——易感类，该类成员没有染上新型冠状病毒，也没有免疫能力，可以被传染上新型冠状病毒，设易感类人群t时刻在总人口中所占比例为s（t），S（t）=Ns（t）；
I——感染者，该类成员已经成为真正的新型冠状病毒患者，能够把病毒传染给S类成员，设该类人群t时刻在总人口中的比例为i（t），I（t）=Ni（t）；
R——免疫类，该类成员为新型冠状病毒康复者或因患病死亡，已经具有免疫力，不再对其他成员产生任何影响，设该类人群t时刻在总人口中的比例为r（t），R（t）=N*r（t）；
a——在t时刻单位时间内被所有病人传染的人数为aNs(t)i(t)；
b——在t时刻单位时间内恢复者数量为bNi(t)。
感染机制：
在这里插入图片描述
上面第一个式子表示感染者的总人数为原有感染者的人数I（j）加上原有易感者S（i）被感染产生的I（i），a是感染率
第二个式子表示新增的移出者

易感者患病到移出的过程可用如下微分方程表示：在这里插入图片描述

模型求解

数据选取
我选取了河南省一月二十一日到二月二十日的数据来进行模型的建立和验证
（全部的数据的和代码会放在附件里：）
要得到sir方程的解析解十分困难，可借助matlab解得其数值解进行分析和预测，预测的关键在于感染系数a与恢复系数b的取值。

%该部分用于计算移出率b
%data1 是河南省1,21到2.20的数据   data是2.1到2.20的数据
load data1
for n = 1:length(r)-1r0(n) = (r(n+1) - r(n))./i(n);
end
b = mean(r0)%b取data数据结果为0.035 取data1数据结果为0.024 故在以后的程序中b取0.03

求解恢复系数b
查阅资料可知在以往的模型中常取恢复天数的倒数作为恢复系数，但是就当下情况来看无法获取本次疫情确切的恢复天数，所以我们在n天的样本中使用（当天的移出人数r（n）减去第二天的移出人数r（n+1））/当天的确诊者人数i（n），以此循环n-1次求平均得到恢复系数b，但是考虑到疫情在河南开始初始，当地对于病毒的检测手段治愈方法都相对落后，有一些感染者未被及时发现，以及恢复时间偏长。所以我们使用1.21到2.20的数据算出b1，再使用2.1到2.20的数据算出b2，将b1，b2取平均值得到b，这样我们赋予了后二十天的数据两倍的权重，可以对冲掉一部分因为前十一天数据的精度而产生的误差。最终我们得到b的取值为0.03。查阅资料得到2003年非典疫情的恢复时间为22天，而两次疫情有着很大的相似性，所以可见所求的恢复系数b据有一定的可信度。

function [ y ] = sir(t,x)
%描述sir模型的微分方程
%数组x前三个值分别为s i r初值，后两个值存储感染系数a 恢复系数b
y=[-x(4)*x(1)*x(2),x(4)*x(1)*x(2)-x(5)*x(2),x(5)*x(2),0,0]'; %s增长率，i增长率，r增长率
end

%用最小二乘法估计s(t)初值和感染系数a
%data1 是河南省1,21到2.20的数据   data是2.1到2.20的数据
clc
clear
load data.mat
b=0.03;   % 由Nmub计算所得
%该部分用于计算a和s的初值 采用最小二乘法
s0 = 1500:10:30000;  % 估计s初值的取值范围
for n = 1:length(s0)s1 = s0(n) + i(1) - i(2) - r(2);m = (s0(n) - s1)./(s0(n).*i(1));t = 1:8;[T,Y] = ode45('sir',t,[s0(n),i(1),r(1),m,b]);for p = 1:8SE(p) = (Y(p,2) - i(p)).^2;endSEE(n) = sum(SE); %此时的残差平方和
end
[v,address] = min(SEE);
s = s0(address); %残差平方和最小的s(t)初值
s1 = s + i(1) - i(2) - r(2);
m = (s - s1)./(s.*i(1)); %残差平方和最小的感染系数a
tspan = 1:70;
[T,Y] = ode45('sir',tspan,[s,i(1),r(1),m,b]);
a=m*Y(1)
figure(1);
t = 1:length(i);
plot(t,i,'rx-');
hold on;
y = Y(1:length(i),2);
y = y';
plot(t,y,'bo-');
legend('真实值','预测值');
xlabel('日期');ylabel('感染人数');
figure(2);
R = Y(1:length(r),3);
R = R';
plot(t,r,'rx-');
hold on;
plot(t,R,'bo-');
legend('真实值','预测值');
xlabel('日期');ylabel('移出人数');
save finaldat

求解感染率a和初始易感人群s
对于易感人群初值s(0)和感染系数a的估计采用最小二乘估计的方法，最小二乘估计的基本思路是先估计s(0)和a的取值区间，然后寻找区间内计算得到预测值与真实值残差平方和最小的一组值作为估计值进行预测。本方案遍历的s(0)区间为[5000,30000]. 求得感染率a=0.1805 初始易感者s=1520；结果如图

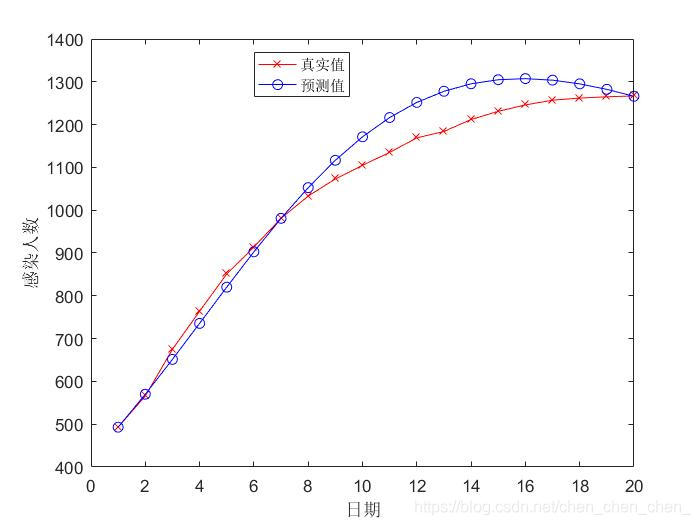
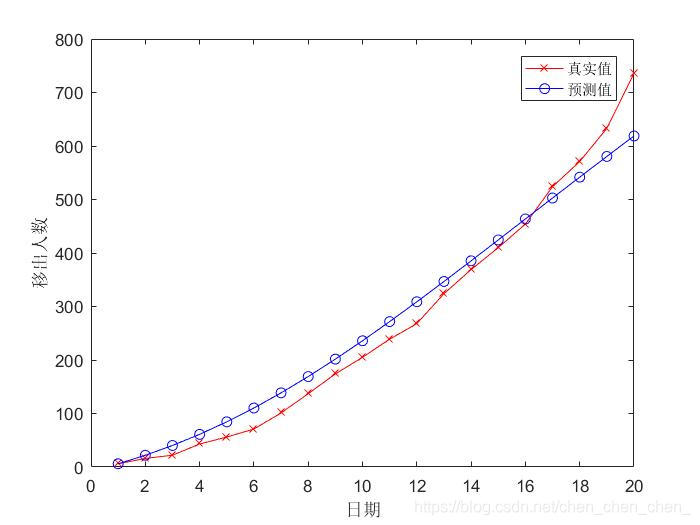在这里插入图片描述这个模型忽略掉了好多因素所以可以看出它把初始的易感人群作为了感染的人口上限，所以在预测的时候有包含峰值时候的数据会好一些

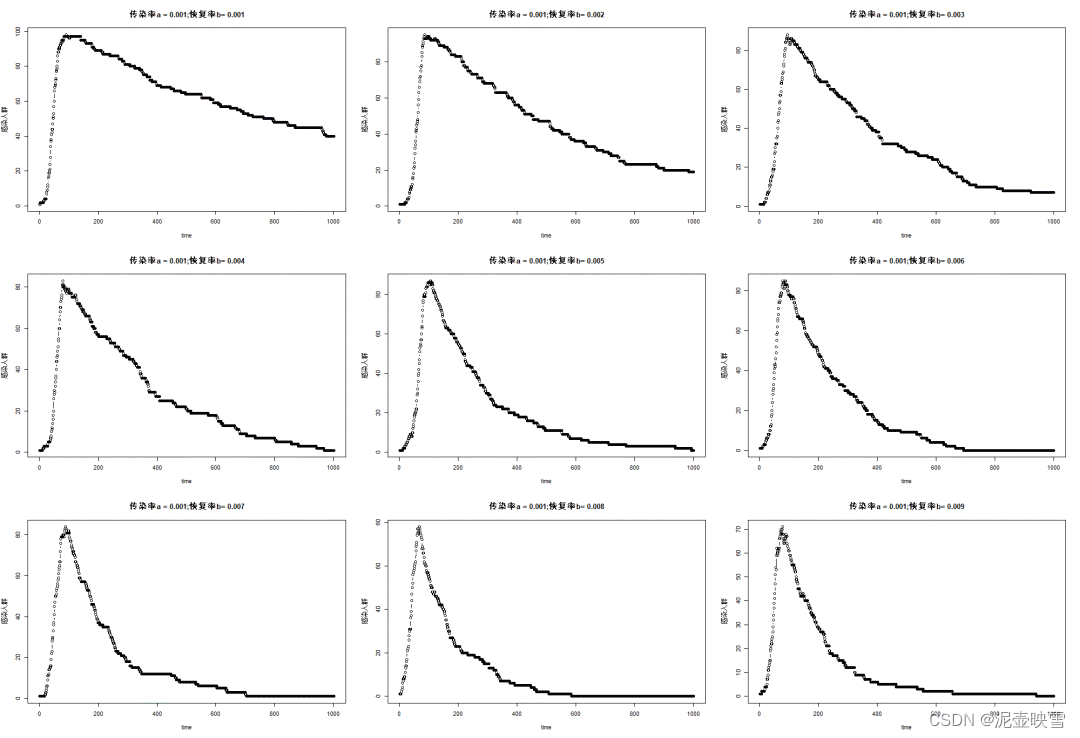
我认为感染率在疫情的发展过程中一直发生着变化，政府加强宣传，人们提高防护意识和卫生习惯，以及相应的隔离措施都可以使感染率减小，而感染率的变化对于疫情的发展有着极大的影响，下面我采用模型在仅感染率发生变化的情况下对于25天内的疫情发展做出预测。

%用最小二乘法估计s(t)初值和感染系数a
%data1 是河南省1,21到2.20的数据   data是2.1到2.20的数据
clc
clear
load data.mat
b=0.03;   % 由Nmub计算所得
%该部分用于计算a和s的初值 采用最小二乘法
s0 = 1500:10:30000;  % 估计s初值的取值范围
for n = 1:length(s0)s1 = s0(n) + i(1) - i(2) - r(2);a = (s0(n) - s1)./(s0(n).*i(1));t = 1:8;[T,Y] = ode45('sir',t,[s0(n),i(1),r(1),a,b]);for p = 1:8SE(p) = (Y(p,2) - i(p)).^2;endSEE(n) = sum(SE); %此时的残差平方和
end
[v,address] = min(SEE);
s = s0(address); %残差平方和最小的s(t)初值
s1 = s + i(1) - i(2) - r(2);
a = (s - s1)./(s.*i(1));%残差平方和最小的感染系数a
tspan = 1:30;
[T,Y] = ode45('sir',tspan,[s,i(1),r(1),a,b]);%a变为原来1/2
a = a/2;
tspan = 1:30;
[T1,Y1] = ode45('sir',tspan,[s,i(1),r(1),a,b]);%a变为原来2倍
a = a*4;
tspan = 1:30;
[T2,Y2] = ode45('sir',tspan,[s,i(1),r(1),a,b]);figure(1);
t = 1:25;
y = Y(1:25,2);
y = y';
plot(t,y,'bo-');
hold on;y1 = Y1(1:25,2);
y1 = y1';
plot(t,y1,'rx-');y2 = Y2(1:25,2);
y2 = y2';
plot(t,y2,'yx-');legend('原感染率','原感染率/2','原感染率*2');
xlabel('日期');ylabel('感染人数');
title('不同感染率下25天内疫情趋势预测')

在这里插入图片描述
如图可以看出随着感染率的增加，感染人数上升更快并且峰值更大，以上预测中在第十天时感染率为a，a/2，2*a的情况下感染人数分别为1171，756，1567。可见各种防疫措施对于疫情的发展的确意义重大。