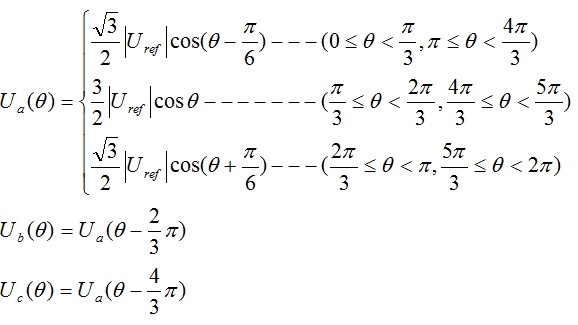小猫爪:PMSM之FOC控制04-SVPWM
- 1 SVPWM的引出
- 2 SVPWM的原理
- 3 SVPWM的推导
- 4 仿真
- END
1 SVPWM的引出
在Park变换那一节,说到了可以通过控制Eq(Iq)和Ed(Id)来控制电机。而电流我们并不能直接控制,只能简介通过控制输出电压来控制电流,这个时候就需要通过经典的反馈控制来实现了。当我们拿到转子的位置时,就可以根据转子位置对电机三相电流进行解耦,经过Clark和Park变换得到反馈信号Id_feedback和Iq_feedback,再通过PID控制器对Id_feedback和Iq_feedback进行分别控制来得到最佳的控制信号,即电压信号Ud和Uq。
根据上面我们就可以列出下面的foc控制的框图:

电流反馈信号经过Clark和Park变换变成Id_feedback和Iq_feedback后,再输入给PID控制器,再使用反Park变换把PID控制器输出的控制信号Ud和Uq变换成Uα和Uβ,然后再将Uα和Uβ送入SVMPWM中产生三相全桥逆变器控制信号控制逆变器产生控制电流。这就是FOC控制流程。
那么Uα和Uβ怎么最终怎么变成逆变器的PWM控制信号呢,这就需要SVPWM来完成了。即SVPWM模块的输入是Uα和Uβ,输出则是PWM信号。
2 SVPWM的原理
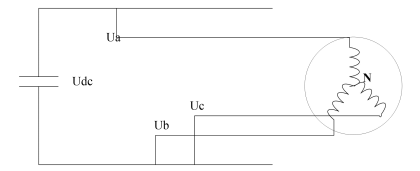
SVPWM 的理论基础是平均值等效原理, 即在一个开关周期内通过对基本电压矢量加以组合, 使其平均值与给定电压矢量相等。 下图为三相全桥逆变器拓扑:

由于逆变器三相桥臂共有 6 个开关管, 为了研究各相上下桥臂不同开关组合时逆变器输出
的空间电压矢量, 特定义开关函数 Sx ( x = a、 b、 c) 为:
S ( x ) = { 1 , 上桥臂导通 0 , 下桥臂导通 S(x)= \begin{cases} 1, & \text {上桥臂导通} \\ 0, & \text{下桥臂导通} \end{cases} S(x)={1,0,上桥臂导通下桥臂导通
(Sa、 Sb、 Sc)的全部可能组合共有八个, 包括 6 个非零矢量 Ul(001)、 U2(010)、 U3(011)、U4(100)、 U5(101)、 U6(110)、 和两个零矢量 U0(000)、U7(111),下面以其中一 种开关 组合为例分 析, 假设 Sx ( x= a、 b、 c)= (100),此时:
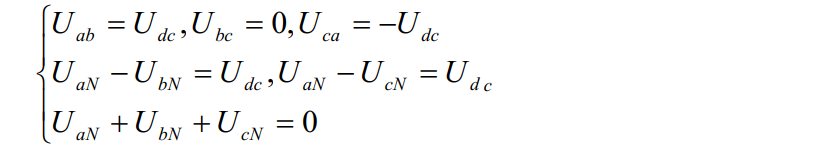
求解上述方程可得: Uan=2Udc/3、 UbN=-Udc/3、 UcN=-Udc/3。 同理可计算出其它各种组合下的空间电压矢量, 列表如下:
| Sa | Sb | Sc | 矢量符号 | Uab | Ubc | Uca | UaN | UbN | UcN |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | U0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | U4 | Udc | 0 | 0 | 2 3 U d c { \frac{2}{3} }Udc 32Udc | − 1 3 U d c {- \frac{1}{3} }Udc −31Udc | − 1 3 U d c {- \frac{1}{3} }Udc −31Udc |
| 1 | 1 | 0 | U6 | Udc | Udc | 0 | 1 3 U d c { \frac{1}{3} }Udc 31Udc | 1 3 U d c {\frac{1}{3} }Udc 31Udc | − 2 3 U d c {- \frac{2}{3} }Udc −32Udc |
| 0 | 1 | 0 | U2 | 0 | Udc | Udc | − 1 3 U d c { -\frac{1}{3} }Udc −31Udc | 2 3 U d c {\frac{2}{3} }Udc 32Udc | − 1 3 U d c {- \frac{1}{3} }Udc −31Udc |
| 0 | 1 | 1 | U3 | 0 | Udc | Udc | − 2 3 U d c {- \frac{2}{3} }Udc −32Udc | 1 3 U d c {\frac{1}{3} }Udc 31Udc | 1 3 U d c {\frac{1}{3} }Udc 31Udc |
| 0 | 0 | 1 | U1 | 0 | 0 | Udc | − 1 3 U d c {- \frac{1}{3} }Udc −31Udc | − 1 3 U d c {- \frac{1}{3} }Udc −31Udc | 2 3 U d c { \frac{2}{3} }Udc 32Udc |
| 1 | 0 | 1 | U5 | Udc | 0 | 0 | 1 3 U d c { \frac{1}{3} }Udc 31Udc | − 2 3 U d c {- \frac{2}{3} }Udc −32Udc | 1 3 U d c {\frac{1}{3} }Udc 31Udc |
| 1 | 1 | 1 | U7 | 0 | 0 | 0 | 0 | 0 | 0 |
| 然后根据这8个情况下分别计算电压合成矢量,则对应的基本电压矢量大小和方向: | |||||||||
 | |||||||||
| 其中非零矢量的幅值相同(模长为 2Udc/3), 相邻的矢量间隔 60° , 而两个零矢量幅值为零, 位于中心。 在每一个扇区, 选择相邻的两个电压矢量以及零矢量, 按照伏秒平衡的原则来合成每个扇区内的任意电压矢量, 即: | |||||||||
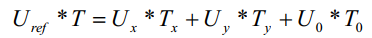 | |||||||||
| 其中, Uref 为期望电压矢量; T 为采样周期; Tx,Ty,T0 分别为对应两个非零电压矢量 Ux、 Uy 和零电压矢量 U 0 在一个采样周期的作用时间,即T=Tx+Ty+T0; 其中 U0 包括了 U0 和 U7 两个零矢量。 矢量 Uref 在 T 时间内所产生的积分效果值和 Ux、 Uy、 U0分别在时间 Tx,Ty,T0 内产生的积分效果相加总和值相同。 |
由于三相正弦波电压在电压空间向量中合成一个等效的旋转电压, 其旋转速度是输入电源角频率, 等效旋转电压的轨迹将是上面所示的圆形。 所以要产生三相正弦波电压,可以利用以上电压向量合成的技术, 在电压空间向量上, 将设定的电压向量由 U4(100)位置开始, 每一次增加一个小增量, 每一个小增量设定电压向量可以用该区中相邻的两个基本非零向量与零电压向量予以合成, 如此所得到的设定电压向量就等效于一个在电压空间向量平面上平滑旋转的电压空间向量, 从而达到电压空间向量脉宽调制的目的。
3 SVPWM的推导
上面说到,只需要算出 Tx,Ty,T0 ,就可以使用相联的两个电压矢量合成任何一个想要的电压状态,换句话说也就是说任何一组Uα和Uβ都可以使用两个相联的电压矢量合成。下面最重要的就是怎么算出 Tx,Ty,T0。
假设欲合成的电压向量 Uref 在第Ⅰ 区中第一个增量的位置, 如图 2-10 所示, 欲用 U4、U6、 U0 及 U7 合成, 用平均值等效可得: U refTz =U4T4 + U6*T6 :

如图可以列出等式:
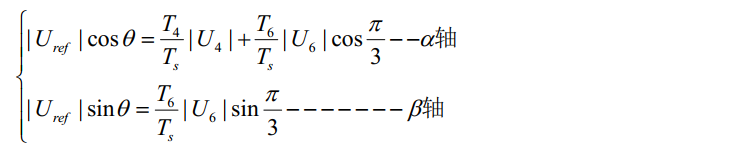
再加上:
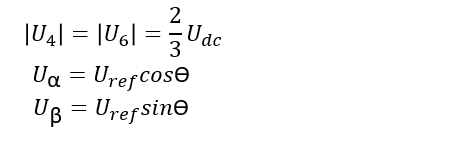
即可算出:
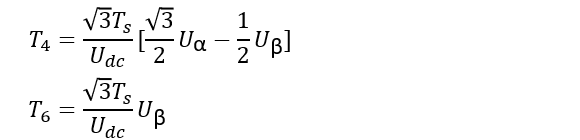
既然Tx,Ty已经求出,则T0=Ts-Tx-Ty。同理即可得出其余六个扇区的值:
| 扇区 | Tx | Ty |
|---|---|---|
| 1 | 3 T S U d c ( 3 2 U α − 1 2 U β ) \frac{\sqrt{{ 3 }}T_S }{U_{dc}}(\frac{\sqrt{{ 3 }} }{2}U_{\alpha}-\frac{{1} }{2}U_{\beta}) Udc3TS(23Uα−21Uβ) | 3 T S U d c U β \frac{\sqrt{{ 3 }}T_S }{U_{dc}}U_{\beta} Udc3TSUβ |
| 2 | − 3 T S U d c ( 3 2 U α − 1 2 U β ) -\frac{\sqrt{{ 3 }}T_S }{U_{dc}}(\frac{\sqrt{{ 3 }} }{2}U_{\alpha}-\frac{{1} }{2}U_{\beta}) −Udc3TS(23Uα−21Uβ) | − 3 T S U d c ( − 3 2 U α − 1 2 U β ) -\frac{\sqrt{{ 3 }}T_S }{U_{dc}}(-\frac{\sqrt{{ 3 }} }{2}U_{\alpha}-\frac{{1} }{2}U_{\beta}) −Udc3TS(−23Uα−21Uβ) |
| 3 | 3 T S U d c U β \frac{\sqrt{{ 3 }}T_S }{U_{dc}}U_{\beta} Udc3TSUβ | 3 T S U d c ( − 3 2 U α − 1 2 U β ) \frac{\sqrt{{ 3 }}T_S }{U_{dc}}(-\frac{\sqrt{{ 3 }} }{2}U_{\alpha}-\frac{{1} }{2}U_{\beta}) Udc3TS(−23Uα−21Uβ) |
| 4 | − 3 T S U d c U β -\frac{\sqrt{{ 3 }}T_S }{U_{dc}}U_{\beta} −Udc3TSUβ | − 3 T S U d c ( 3 2 U α − 1 2 U β ) -\frac{\sqrt{{ 3 }}T_S }{U_{dc}}(\frac{\sqrt{{ 3 }} }{2}U_{\alpha}-\frac{{1} }{2}U_{\beta}) −Udc3TS(23Uα−21Uβ) |
| 5 | 3 T S U d c ( − 3 2 U α − 1 2 U β ) \frac{\sqrt{{ 3 }}T_S }{U_{dc}}(-\frac{\sqrt{{ 3 }} }{2}U_{\alpha}-\frac{{1} }{2}U_{\beta}) Udc3TS(−23Uα−21Uβ) | 3 T S U d c ( 3 2 U α − 1 2 U β ) \frac{\sqrt{{ 3 }}T_S }{U_{dc}}(\frac{\sqrt{{ 3 }} }{2}U_{\alpha}-\frac{{1} }{2}U_{\beta}) Udc3TS(23Uα−21Uβ) |
| 6 | − 3 T S U d c ( − 3 2 U α − 1 2 U β ) -\frac{\sqrt{{ 3 }}T_S }{U_{dc}}(-\frac{\sqrt{{ 3 }} }{2}U_{\alpha}-\frac{{1} }{2}U_{\beta}) −Udc3TS(−23Uα−21Uβ) | − 3 T S U d c U β -\frac{\sqrt{{ 3 }}T_S }{U_{dc}}U_{\beta} −Udc3TSUβ |
计算到这里,有一点非常重要,当两个零电压矢量作用时间为 0 时,此时的合成空间电压矢量幅值最大, 其幅值最大不会超过图中所示的正六边形边界。 而当合成矢量落在该边界之外 时, 将发生过调制, 逆变器输出电压波形将发生失真。 在 SVPWM 调制模式下, 逆变器能够输出的最大不失真圆形旋转电压矢量为下图所示虚线正六边形的内切圆,如下图所示:

如果发现了计算出的时间总和一旦大于单个周期,即Tx+Ty>Ts(六边形界限), Tx+Ty> 3 2 \frac{\sqrt{{ 3 }} }{2} 23Ts(内切圆界限),这个时候就需要进行等比缩小。让最终的Tx+Ty不大于Ts或者 3 2 \frac{\sqrt{{ 3 }} }{2} 23Ts。
每个扇区的时间根据Uα和Uβ都已经计算出来了,但是还有一个需要注意的是怎样通过Uα和Uβ算出当前处在哪个扇区区间内?
不妨再仔细看上表,发现了有三个元素出现频率非常高,分别是:

因为时间肯定是正的,所以让Tx>0, Ty>0,即可列出在每个扇区中保证时间是正的充分必要条件U1,U2,U3是否大于0。若 U1>0 , 则 A=1, 否则 A=0; 若 U 2>0 , 则 B=1, 否则 B=0; 若 U3>0 ,则 C=1, 否则 C=0。 令 N=4C+2B+A,则可以得出如下结论:
| 扇区号 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| N值 | 3 | 1 | 5 | 4 | 6 | 2 |
| 这样就通过Uα和Uβ计算出扇区,决定使用哪两个相连的电压矢量以及各自作用的时间,还有最后一个问题,怎么把时间变成我们想要的PWM波。 |
最常用的SVPWM调制方式有两种,7段式和5段式,顾名思义就是在一个扇区中,开关状态一共有7种状态或者5种状态,下面我们就以最常见的7段式作说明:
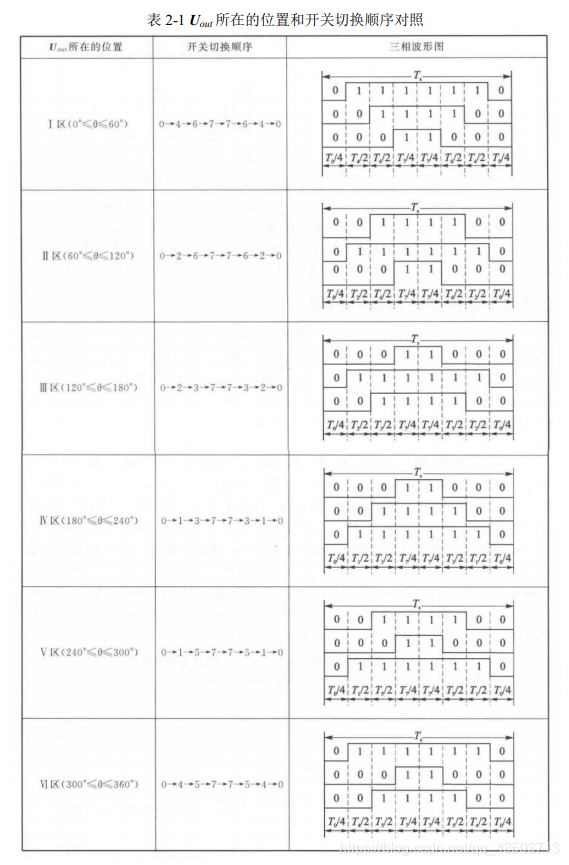
以减少开关次数为目标, 将基本矢量作用顺序的分配原则选定为: 在每次开关状态转换时, 只改变其中一相的 开关状态。 并且对零矢量在时间上进行了平均分配, 以使产生的 PWM 对称, 从而有效地降低 PWM 的谐波分量。
当 U4(100)切换至 U0(000)时, 只需改变 A 相上下一对切换开关, 若由 U4(100)切换至 U7(111)则需改变 B、 C 相上下两对切换开关, 增加了一倍的切换损失。 因此要改变电压向量 U4(100)、 U2(010)、 U1(001)的大小,需配合零电压向量 U0(000), 而要改变 U6(110)、 U3(011)、 U5(101), 需配合零电压向量U7(111)。 这样通过在不同区间内安排不同的开关切换顺序, 就可以获得对称的输出波形。
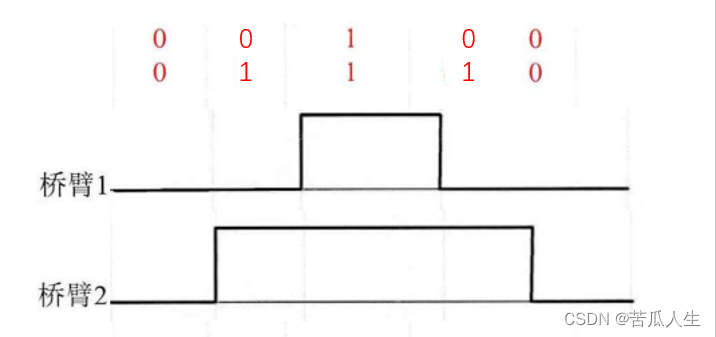
以第一个扇区为例:开关状态切换和PWM波形,以及每个开关状态相应的作用时间如下图:

可以看出在第一扇区中,一次经历了0-4-6-7-7-6-4-0这七种开关状态,两种开关状态之间的切换只改变了一组开关状态。依次类推,其他扇区也是这样的,这里就不多做什么,了解到7段式调制的原理,接下来就是怎样把算出的时间转换成MCU外设中的比较器值了,让MCU按照需求输出正确时间的PWM波形了。
这一般跟MCU的PWM生成模块相关,就以最常见的center-align举例吧。在 I 扇区时如下图:

三个PWM高电平时间值为:
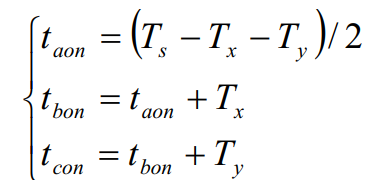
对应的计数器的比较值为:

其中TNx和Tx的对应关系为:TNx = NTPWM*Tx/Ts。
以此类推,得到其他扇区的比较器值如下表所示:

注:当然了,由于现在各家MCU厂商的SDK驱动库比较全面,一般都有直接设置占空比的函数,所以也可以让SVPWM输出三个占空比信号直接传参给驱动函数就好了,这样会更加简单。确定好PWM的周期之后,直接将三个信号的占空比算出即可,当然还是仅限center-align的这种对称工作模式。
到这里为止,SVPWM就全部介绍完了。
4 仿真
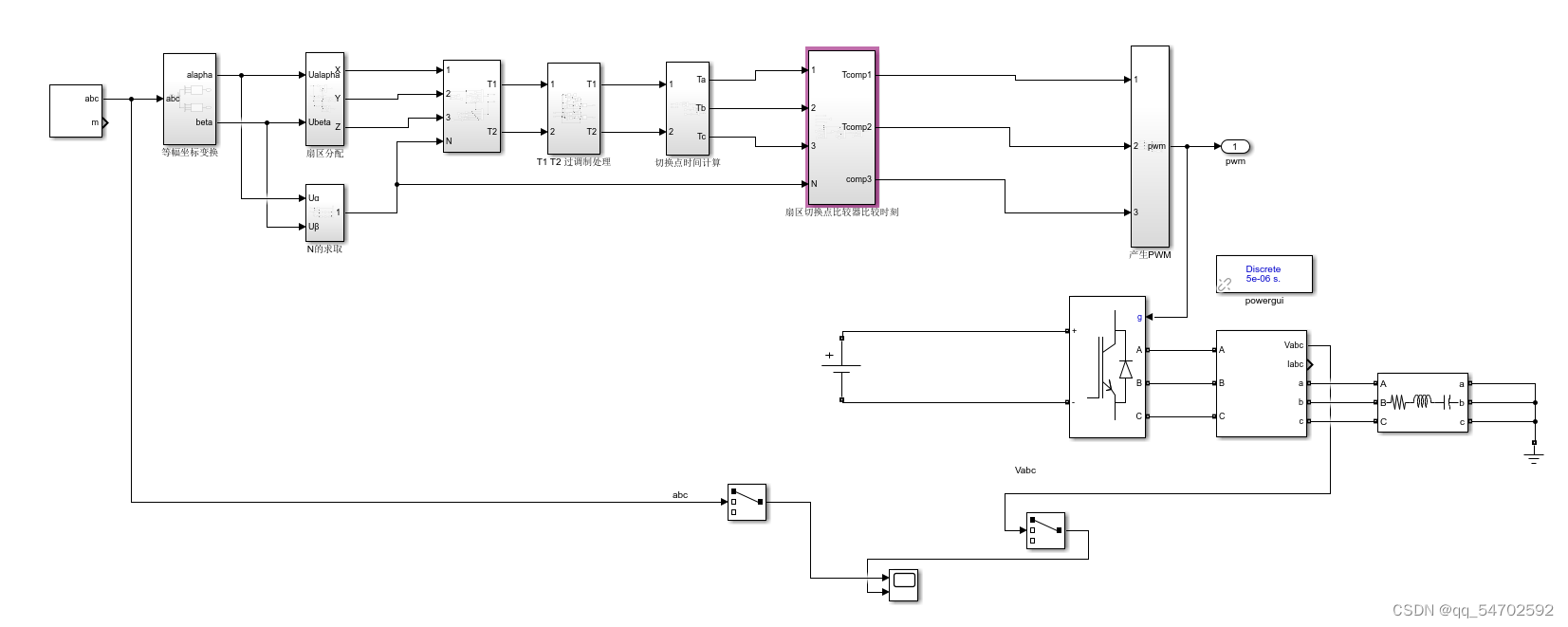
根据上面的推导直接整出仿真:

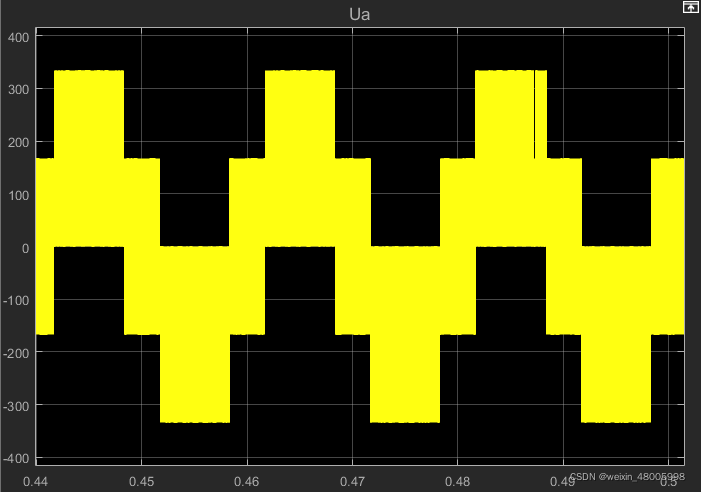
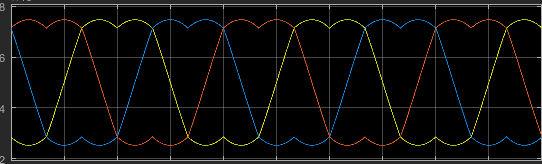
仿真结果比较值输出:

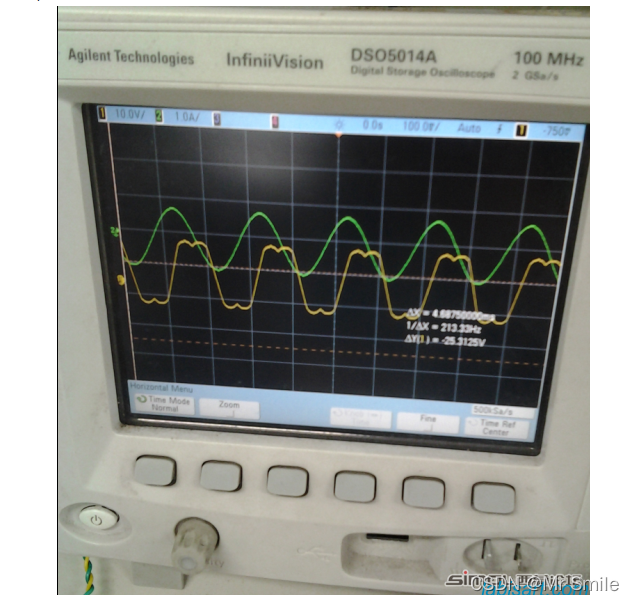
如果是这种马鞍形状,那么就代表成功了,接下来就是将其移植到MCU中,让其输出正确的PWM波了。将算法使用MATLAB生成并移植到MCU中,打印出比较器的值如下:

在MCU中也验证正确了。