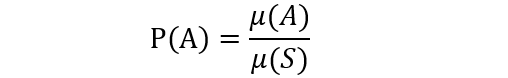排列组合

排列组合高中应该就学过，包括两个原理（加法和乘法原理），以及排列和组合

两个原理

加法原理
比如完成某件事有3类途径，在1类中有4种方法，第2类中有2种方法，第3类中有3种方法，那么完成这件事有4+2+3种不同的方法：

完成某件事需要n个步骤，每个步骤之间有关联（不独立），第一个步骤有m种方法，而对应于第一个步的第k个方法，第二个步骤有$m_k$种方法，那么完成这件事共有${\sum }_{k=1}^m{m}_k$种方法

乘法原理
比如完成某件事需要2个步骤，第一个步骤有3种方法，第二个步骤有2种方法，那么完成这件事共有3x2种方法：

完成某件事需要n个步骤，每个步骤之间没有关联（独立），第k个步骤有$m_k$种方法，那么完成这件事共有${\prod }_{k=1}^n{m}_k$种方法

---

可以将仅有2个步骤的乘法原理过程看成1个特殊的加法原理过程，其特殊在于第一个步的第k个方法，第二个步骤有$m_k$种方法，并且对于任意$m_k$都相等。

排列与组合

从n个不同元素中取出r个，排成一排，称为一个排列，亦称为有序抽样

若取出r个元素不允许重复（不放回抽样），由乘法原理可知排列方式有$A_n^r$种：
$A_n^r=n(n-1)...(n-r+1)=\frac{n!}{(n-r)!}$
当$r<n$时为选排列，当$r=n$时为全排列，且$A_n^n=n!$

---

若取出r个元素允许重复（有放回抽样），由乘法原理可知排列方式有 $n^r$ 种

从n个不同元素中取出r个，作为一组，称为一个组合，亦称为无序抽样

可以将其看成一个无序的排列，取出r个的排列总数除以每个排列可交换顺序次数。
若取出r个元素不允许重复（不放回抽样），则组合数为：
$C_n^r=\frac{A_n^r}{r!}=\frac{n!}{r!(n-r)!}$
等式组合：
$C_n^r=C_n^{n-r}$

---

若取出r个元素允许重复（有放回抽样），则可以采用拔靴法（Bootstrapping）：
\qquad
假设集合 S = { w 1 , w 2 , w 3 } S=\{w_1,w_2,w_3\} S={w1​,w2​,w3​},有放回无序抽样$r=2$个，共有多少种结果 ？(求全集数量)
( 注，下列结果中“,”不用来表示先后顺序，B表示计数桶，当$B=(x_1，x_2，x_3)$时表示$w_1$个数为$x_1$，$w_2$个数为$x_2$，$w_3$个数为$x_3$。)
\qquad
1、$B=(2，0，0)$$\to$ { w 1 , w 1 } \{w_1,w_1\}\qquad {w1​,w1​} 2、$B=(0，2，0)$$\to$ { w 2 , w 2 } \{w_2,w_2\} {w2​,w2​}
3、$B=(0，0，2)$$\to$ { w 3 , w 3 } \{w_3,w_3\}\qquad {w3​,w3​} 4、$B=(1，1，0)$$\to$ { w 1 , w 2 } \{w_1,w_2\} {w1​,w2​}
5、$B=(1，0，1)$$\to$ { w 1 , w 3 } \{w_1,w_3\}\qquad {w1​,w3​} 6、$B=(0，1，1)$$\to$ { w 2 , w 3 } \{w_2,w_3\} {w2​,w3​}
\qquad
我们将上面所有结果用如下方程来表示，在$B=(x_1，x_2，x_3)$中有 ：
\qquad
x 1 + x 2 + x 3 = 2 ， 其 中 x 1 ， x 2 ， x 3 ∈ { 0 , 1 , 2 } \qquad x_1+x_2+x_3=2，\quad其中x_1，x_2，x_3\in\{0,1,2\} x1​+x2​+x3​=2，其中x1​，x2​，x3​∈{0,1,2}
\qquad
将上述情况推广一下，对于集合 S = { w 1 , w 2 . . . . , w n } S=\{w_1,w_2....,w_n\} S={w1​,w2​....,wn​},有放回无序抽样$r$个,结果即为：
\qquad
x 1 + x 2 . . . + x n = r ， 其 中 任 意 x i ∈ { 0 , 1... , r } \qquad x_1+x_2...+x_n=r，\quad其中任意x_i\in\{0,1...,r\} x1​+x2​...+xn​=r，其中任意xi​∈{0,1...,r}
\qquad
但是上述结果是不易求解的，我们将问题转化一下，我们重新用一个桶，编号0~n，分别用来存放抽取出来的杆$w_i$：

我们再简化一下，把桶也去了，只留下分隔栏：

所以栏的数+杆$w_i$的数一共有$n+r-1$个，我们现在有$n+r-1$个孔：

我们现在要做的，要么先将$r$根杆先插入$n+r-1$个孔中，然后用剩下n-1根栏按顺序依次插入空白的孔中。由于只要$r$根杆位置确定了，栏的位置也就确定了。
要么先将$n-1$n-1根栏先插入$n+r-1$个孔中，然后用剩下r根杆按顺序依次插入空白的孔中。由于只要$n-1$根栏位置确定了，杆的位置也就确定了。
\qquad
所以有组合数为：
$C_{n+r-1}^r=\frac{A_{n+r-1}^r}{r!}=\frac{(n+r-1)!}{r!((n+r-1)-r)!}=\frac{(n+r-1)!}{r!(n-1)!}=C_{n+r-1}^{n-1}$

古典概型

古典概型又称为等可能概型，特点如下：

1、基本事件有限
2、基本事件互斥
3、基本事件等可能发生

定义条件：

1、 Ω = { w 1 , w 2 . . . . . w n } , n ≠ ∞ . n = C \Omega= \{w_1,w_2.....w_n\},n\neq \infty.n=C Ω={w1​,w2​.....wn​},n​=∞.n=C
2、$w_i\cap w_j=\varnothing ,i\ne j$
3、$P(w_1)=P(w_2)=P(w_3)...=P(w_n)$
4、$P(\Omega )=1$

性质：

设 A = { w 1 , w 2 . . . . . w m } A= \{w_1,w_2.....w_m\} A={w1​,w2​.....wm​}
则$P(A)=P(w_2)+P(w_3)...+P(w_m)=\frac{m}{n}$

放回抽样与不放回抽样

这个前面排列组合时已经讲过，这里就不再提及，排列组合中分为四种：

1、不放回有序采样 2、放回有序采样
3、不放回无序采样 4、放回无序采样
\qquad
但这四种抽样结果中，并不都属于古典概型，比如第四种，假设新集合$A$为从 S = { w 1 , w 2 } S=\{w_1,w_2\} S={w1​,w2​},有放回无序抽取2个，很显然该集合$A$所有元素为：
\qquad
A = { a 1 , a 2 , a 3 } A=\{a_1,a_2,a_3\} A={a1​,a2​,a3​}， \qquad a 1 = { w 1 , w 1 } , a 1 = { w 2 , w 2 } , a 3 = { w 1 , w 2 } a_1=\{w_1,w_1\},a_1=\{w_2,w_2\},a_3=\{w_1,w_2\} a1​={w1​,w1​},a1​={w2​,w2​},a3​={w1​,w2​}
\qquad
但是$a_3$的概率和$a_1、a_2$的概率并不等，因为$a_3$的结果可以抽到是$(w_1,w_2)$也可以是$(w_2,w_1)$，所以$P(a_1)=P(a_2)=0.25,P(a_3)=0.5$

随机抽样在机器学习中的应用

所以在机器学习中，我们从数据全集中抽取一部分样本进行训练时，采样时就要注意选择抽样方法，抽样结果是否和全集的数据分布特征一致，不一致时又如何处理。

含$n$个样本的训练集的随机放回采样中，一个样本每次被采集到的概率是$\frac{1}{n}$。不被采集到的概率为$1-\frac{1}{n}$。在连续n次采样都没有被采集中的概率是$(1-\frac{1}{n}{)}^n$。
\qquad
当$n\to \infty$时，$(1-\frac{1}{n}{)}^n=\frac{1}{e}\to 0.368$。也就是说，在bagging的每轮随机采样中，训练集中大约有$36.8$的数据没有被采样集采中。对于这部分大约36.8%的没有被采样到的数据，我们常常称之为袋外数据(Out Of Bag, 简称OOB)。这些数据没有参与训练集模型的拟合，因此可以用来检测模型的泛化能力。

几何分布

上面的抽样方式中，利用第四种放回无序的抽样，在对立事件的集合中，可以得到几何分布：

1、集合必须右对立事件构成，比如一个集合中，共有N件产品，且有K件次品，很显然剩下N-K件均为良品。
2、放回抽取r次，求恰好第r次才抽中次品的概率。
\qquad
由于每次抽取都是独立的，所以每次抽到次品概率为$\frac{K}{N}$,良品概率$\frac{N-K}{N}$，由乘法原理我们知道连续抽取r次，前面都抽到了良品，所以根据乘法原理有：

\qquad
$P(r)=(1-p{)}^{r-1}p=(\frac{N-K}{N}{)}^{r-1}(\frac{K}{N})$

二项分布

上面的抽样方式中，利用第四种放回无序的抽样，在对立事件的集合中，可以得到二项分布：

1、集合必须右对立事件构成，比如一个集合中，共有N件产品，且有K件次品，很显然剩下N-K件均为良品。
2、放回抽取r次，且事件A为：r次抽取中，恰有m件次品。

求P（A）为多少？
\qquad
由于每次抽取都是独立的，所以每次抽到次品概率为$\frac{K}{N}$,良品概率$\frac{N-K}{N}$，由乘法原理我们知道连续抽取r次，抽到任意特定情况（比如下图情况）的m件次品和（r-m）件良品的概率为：$(\frac{K}{N}{)}^m(\frac{N-K}{N}{)}^{r-m}=\frac{K^m(N-K{)}^{r-m}}{N^r}$

但由于要求是无序的，所以需要将所有可能的排列算进去，得：
$P(A)=C_r^m{p}^m(1-p{)}^{r-m}=C_r^m(\frac{K}{N}{)}^m(\frac{N-K}{N}{)}^{r-m}=C_r^m\frac{K^m(N-K{)}^{r-m}}{N^r}$

或者也可以理解为：从集合r次抽取构成一个新集合，其中恰有m件次品的样本比例为多少？
\qquad
新集合基本事件总数为$N^r$个,每次从$K$件次品中取1件，取m次共有$K^m$种取法，同理良品有
$(N-K{)}^{r-m}$种取法，由于m件次品在r次抽样中的方式共有$C_r^m$种，所以事件A发生的个数为$C_r^m{K}^m(N-K{)}^{r-m}$，除以基本事件总数即可得到概率：
\qquad
$P(A)=\frac{C_r^m{K}^m(N-K{)}^{r-m}}{N^r}$

超几何分布

上面的抽样方式中，利用第三种不放回无序的抽样，在对立事件的集合中，可以得到超几何分布：

1、集合必须右对立事件构成，比如一个集合中，共有N件产品，且有K件次品，很显然剩下N-K件均为良品。
2、不放回抽取r次，且事件A为：r次抽取中，恰有m件次品。

从集合中取出r件产品作为新集合，新集合样本数为$C_N^r$,在K件次品中取m件，有$C_K^m$种取法，在N-K件次品中取r-m件，有$C_{N-K}^{r-m}$种取法，所以概率为：

$P(A)=\frac{C_K^m{C}_{N-K}^{r-m}}{C_N^r}$
\qquad

几何概型

几何概型也是等可能概型，与古典概型的区别在于基本事件个数，特点如下：

1、基本事件无限
2、基本事件互斥
3、基本事件等可能发生

特征如下：

1、样本空间$S$是一个几何区域，这区域大小可以度量，并记$S$的度量为$m(S)$。
2、落在区域内任意点都是等可能的，落在其内的区域$A$内的可能性与$m(A)$成正比。

事件A发生的概率为：
\qquad
$P(A)=\frac{m(A)}{m(S)}$