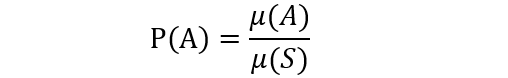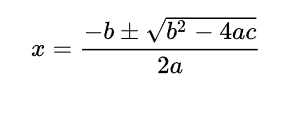概率论对于学习 NLP 方向的人，重要性不言而喻。于是我打算从概率论基础篇开始复习，也顺便巩固巩固基础。

1.事件及运算

1.1 文森图及运算

1.2常用运算律

1.3相关练习

理解：要么A要么B要么C发生，所以是A ∪ B ∪ C； 如果说都发生，那就是A ∩ B ∩ C。

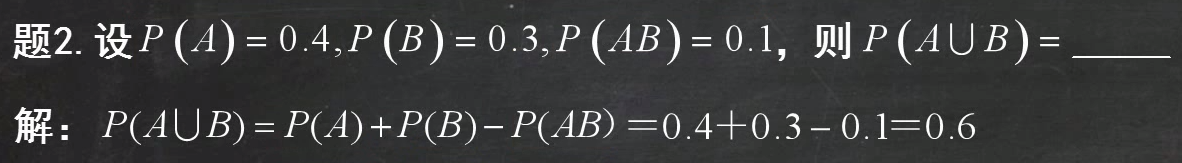
理解：用到了加法公式，直接套进去就可

理解：需要注意的是，这里会用到乘法公式，P（AC）=0，则P（ABC）=0.

理解：这里用到了德摩根律，之后用到了对立事件，再次利用加法公式，又利用互斥的特点，得出结果。

理解：先用加法公式，之后使用独立事件，P（AB）=P（A）P（B），解出答案。

理解：一定要对减法公式的变式敏感，这是减法公式的一种形式。

理解：正确答案为D。P（A-B）= P（A）-P（AB），P（AB）为0，所以等式符合。
互不相容和对立可以推出P（AB）=0，但后者推不出前者，图中有证明。

2.古典概型

古典概型也叫传统概率、其定义是由法国数学家拉普拉斯 (Laplace ) 提出的。如果一个随机试验所包含的单位事件是有限的，且每个单位事件发生的可能性均相等，则这个随机试验叫做拉普拉斯试验，这种条件下的概率模型就叫古典概型。
（1） 试验中所有可能出现的基本事件只有有限个；
（2） 试验中每个基本事件出现的可能性相等。
具有以上两个特点的概率模型是大量存在的，这种概率模型称为古典概率模型，简称古典概型，也叫等可能概型。

2.1相关题目

理解：不要忘记排列和组合的相关公式计算方法。其中分为有放回和无放回。

理解：注意结论的使用，不放回抽样时，概率都是一样的。

3.几何概型

如果每个事件发生的概率只与构成该事件区域的长度(面积或体积或度数)成比例，则称这样的概率模型为几何概率模型，简称为几何概型。
比如：对于一个随机试验，我们将每个基本事件理解为从某个特定的几何区域内随机地取一点，该区域中每一个点被取到的机会都一样；而一个随机事件的发生则理解为恰好取到上述区域内的某个指定区域中的点。这里的区域可以是线段，平面图形，立体图形等。用这种方法处理随机试验，称为几何概型.
几何概型与古典概型相对，将等可能事件的概念从有限向无限的延伸。这个概念在我国初中数学中就开始介绍了。
古典概型与几何概型的主要区别在于：几何概型是另一类等可能概型，它与古典概型的区别在于试验的结果是无限个。

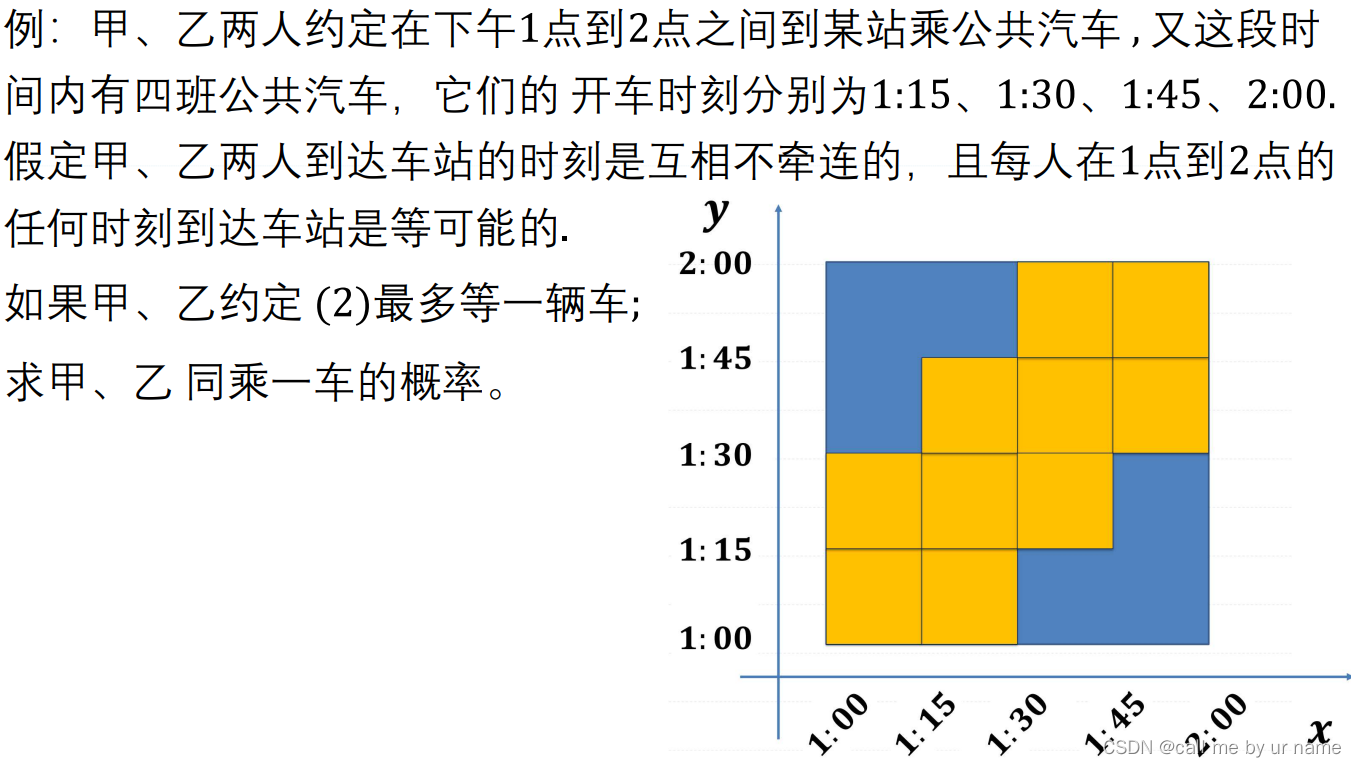
3.1题目

理解：这个比较简单，根据其长度之比就可以

理解：最主要的在于判断时间转换为数学公式的过程，之后利用几何概型就可以解决