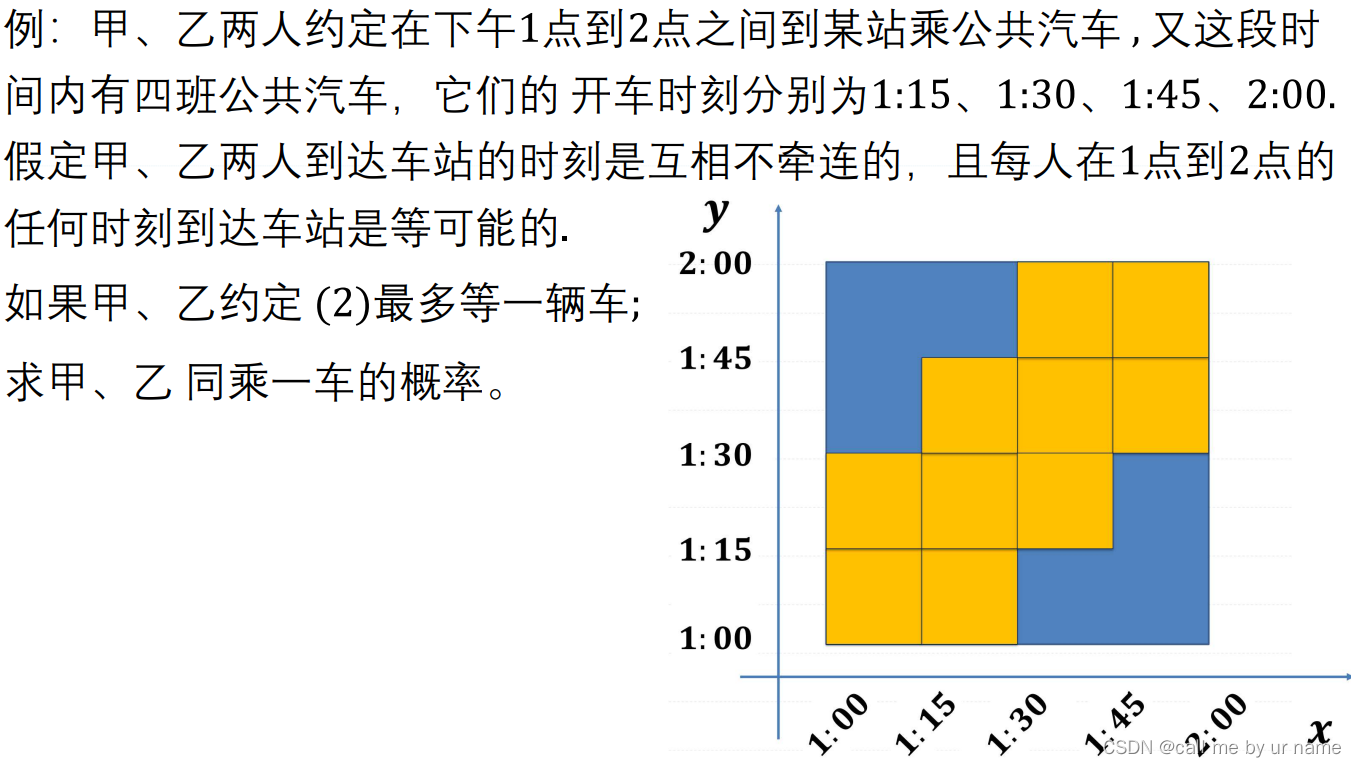
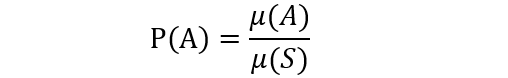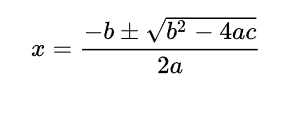假定以$S$为样本空间的随机试验是一个等概模型，事件$A\subseteq S$。若能算得$|S|=n$，$|A|=m$，我们知道$P(A)=m/n$。我们把这样的计算方法定义成下列的Python函数。

from sympy import Rational  #导入Rational
def P(A, S):	            #等概模型下事件A的概率n = len(S)	            #S所含元素个数m = len(A)	            #A所含元素个数return Rational(m, n)   #返回m/n的分数形式

结合程序中行内注释信息，不难理解上述程序。第3、4两行调用Python的len函数，分别计算由参数传递而来的S和A所含的元素个数n和m。第5行用m和n创建表示m/n的分数形式的Rational（sympy包中表示有理数的数据类型，第1行导入）对象并返回。
例1 将一枚均匀硬币抛掷三次，用上面定义的P函数计算事件$A_1$：“恰有一次出现正面”和$A_2$：“至少有1次出现正面”的概率$P(A_1)$和$P(A_2)$。
解： 若将分币的正面朝上记为1，正面朝下记为0，该随机试验的样本空间$S=\{(0,0,0),(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,0),(1,1,1)\}$，即集合 { 0 , 1 } \{0,1\} {0,1}中取3个元素可重排列的全体。故$|S|=8$。由于硬币是均匀的，所以每个样本点是等概的。事件“恰有一次出现正面”$A_1=\{(0,0,1),(0,1,0),(1,0,0)\}$，故$|A_1|=3$。
$$P(A_1)=|A_1|/|S|=3/8$$
事件“至少有1次出现正面” $A_2$的对立事件为“一次正面都没有出现”，即${\bar{A}}_2=\{(0,0,0)\}$。故$|{\bar{A}}_2|=1$，于是$P({\bar{A}}_2)=1/8$。而
$$P(A_2)=1-P({\bar{A}}_2)=1-1/8=7/8$$
下列代码完成验算。

from sympy.utilities.iterables import variations as permutations#导入permutations
S=set(permutations([0, 1], 3, True))           					#构造样本空间S
A1 = subSet(S, lambda a: sum(a) == 1)        					#设置事件A1
p1 = P(A1, S)                                  					#计算事件A1的概率p1
print('P(A1)=%s' % p1)                         					#输出p1
A2 = setSet(S, lambda a: 1 in a)             					#设置事件A2
p2 = P(A2, S)                                  					#计算事件A2的概率p2
print('P(A2)=%s' % p2)                         					#输出p2

程序中第2行调用permutations函数（第1行导入，详见博文《排列组合——构造样本空间》）设置抛掷3次分币试验的样本空间S，其中的样本点为三元组(i, j, k)，每个分量均取1（正面朝上）或0（正面朝下）。第3行调用函数subSet（定义见博文《按条件设置随机事件》），传递参数lambda a: sum(a)==1设置事件A1，第4行调用上面定义的计算等概模型中事件概率的函数P，用传递给它的参数A1和S计算A1的概率p1。第5行输出p1的值。相仿地，第8~10行分别设置事件A2，计算A2的概率p2，输出p2。运行程序，输出：

P(A1)=3/8
P(A2)=7/8

例2房间里有10个人，各自编号1~10，任选3人记录其编号。计算事件$A_1$：3人中最小编号为5，$A_2$：3人最大编号为5的概率$P(A_1)$和$P(A_2)$。
解： 在10个人中选择3人，共有$C_{10}^3$种不同的选法，即样本空间含有的样本点数$|S|=C_{10}^3=120$。又由于3人是任选的，所以每个选法发生的可能性是相同的。这是一个古典概型。事件$A_1$：所选3人中最小编号为5，意味着编号为5者必在此3人中。其余两人的编号应该比5大，共有$C_5^2=10$种选择方法，即$|A_1|=10$。于是
$$P(A_1)=|A_1|/|S|=C_5^2/C_{10}^3=10/120=1/12$$
相仿地，事件$A_2$：3人最大编号为5所含样本点数$|A_2|=C_4^2=6$。于是
$$P(A_2)=|A_2|/|S|=C_4^2/C_{10}^3=6/120=1/20.$$
下列代码完成验算

from sympy.utilities.iterables import subsets as combinations	#导入subsets
numbers=[1,2,3,4,5,6,7,8,9,10]                  				#房内10人的编号
S=set(combinations(numbers, 3))                 				#构造样本空间S          
A1=subSet(S, lambda a: min(a)==5)             				    #3人中最小号码为5
p1=P(A1, S)
print('P(A1)=%s'%p1)
A2=subSet(S, lambda a: max(a)==5)             				    #3人中最大号码为5
p2=P(A2, S)
print('P(A2)=%s'%p2)

第2行将10个编号1,2,…,10设为列表numbers，第4行调用函数combinations（第1行导入，详见博文《排列组合——构造样本空间》），构造从numbers中任取3个的所有组合作为样本空间S。第4行函调用数subSet设置事件$A_1$，最小号码为5；相仿地，第7行调用subSet函数设置事件$A_2$，最大号码为5。运行程序，输出：

P(A1)=1/12
P(A2)=1/20

写博不易，敬请支持：
如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！
返回《导引》