插件介绍
Sublime Text 3 安装Package Control
原来Subl3安装Package Control很麻烦,现在简单的方法来了
一、简单的安装方法
使用 Ctrl+`快捷键或者通过 View->Show Console菜单打开命令行,粘贴如下代码:
import urllib.request,os; pf = 'Package Control.sublime-package'; ipp = sublime.installed_packages_path(); urllib.request.install_opener( urllib.request.build_opener( urllib.request.ProxyHandler()) );open(os.path.join(ipp, pf), 'wb').write(urllib.request.urlopen('http://sublime.wbond.net/' + pf.replace(' ','%20')).read())
如果顺利的话,此时就可以在Preferences菜单下看到Package Settings和Package Control两个菜单了。
顺便贴下Sublime Text2 的代码:
import urllib2,os; pf='Package Control.sublime-package'; ipp = sublime.installed_packages_path(); os.makedirs( ipp ) if not os.path.exists(ipp)else None; urllib2.install_opener( urllib2.build_opener( urllib2.ProxyHandler( ))); open( os.path.join( ipp, pf), 'wb' ).write( urllib2.urlopen( 'http://sublime.wbond.net/' +pf.replace(' ','%20' )).read());print('Please restart Sublime Text to finish installation')
二、手动安装
可能由于各种原因,无法使用代码安装,那可以通过以下步骤手动安装Package Control:
1.点击Preferences > Browse Packages菜单
2.进入打开的目录的上层目录,然后再进入Installed Packages/目录
3.下载Package Control.sublime-package并复制到Installed Packages/目录(地址:https://sublime.wbond.net/Package%20Control.sublime-package)
4.重启Sublime Text。
原来Subl3安装Package Control很麻烦,现在简单的方法来了
一、简单的安装方法
使用 Ctrl+`快捷键或者通过 View->Show Console菜单打开命令行,粘贴如下代码:
import urllib.request,os; pf = 'Package Control.sublime-package'; ipp = sublime.installed_packages_path(); urllib.request.install_opener( urllib.request.build_opener( urllib.request.ProxyHandler()) );open(os.path.join(ipp, pf), 'wb').write(urllib.request.urlopen('http://sublime.wbond.net/' + pf.replace(' ','%20')).read())
如果顺利的话,此时就可以在Preferences菜单下看到Package Settings和Package Control两个菜单了。
顺便贴下Sublime Text2 的代码:
import urllib2,os; pf='Package Control.sublime-package'; ipp = sublime.installed_packages_path(); os.makedirs( ipp ) if not os.path.exists(ipp)else None; urllib2.install_opener( urllib2.build_opener( urllib2.ProxyHandler( ))); open( os.path.join( ipp, pf), 'wb' ).write( urllib2.urlopen( 'http://sublime.wbond.net/' +pf.replace(' ','%20' )).read());print('Please restart Sublime Text to finish installation')
二、手动安装
可能由于各种原因,无法使用代码安装,那可以通过以下步骤手动安装Package Control:
1.点击Preferences > Browse Packages菜单
2.进入打开的目录的上层目录,然后再进入Installed Packages/目录
3.下载Package Control.sublime-package并复制到Installed Packages/目录(地址:https://sublime.wbond.net/Package%20Control.sublime-package)
4.重启Sublime Text。
Emmet
功能:编码快捷键,前端必备
简介:Emmet作为zen coding的升级版,对于前端来说,可是必备插件,如果你对它还不太熟悉,可以在其官网(http://docs.emmet.io/)上看下具体的演示视频。
使用:教程-http://docs.emmet.io/cheat-sheet/、http://peters-playground.com/Emmet-Css-Snippets-for-Sublime-Text-2/
(安装方法:
点击菜单Preference-->Package Control
点击Install Package

等待几秒后再弹出如下内容,敲键盘emmet,选择如下:

在 Emmet 安装完成后,会显示如下屏幕:然后会自动安装PyV8,安装完成,重启 Sublime Text 3。

测试:
重启之后还会看到左下角再次呈现 Loading PyV8 的提示,待其载入完毕,打开一个新文档最后测试,输入指令(不行就再重启一下)
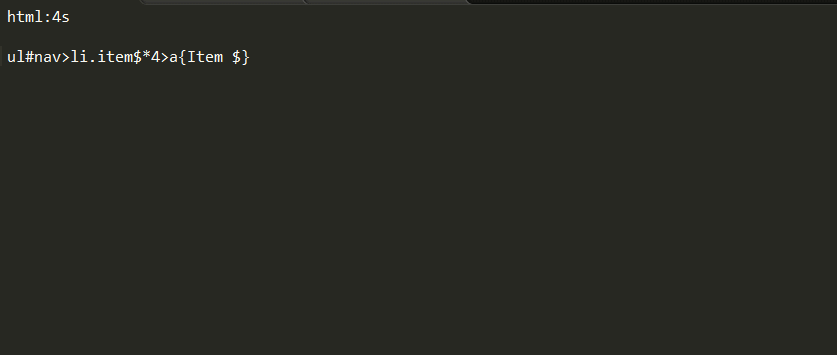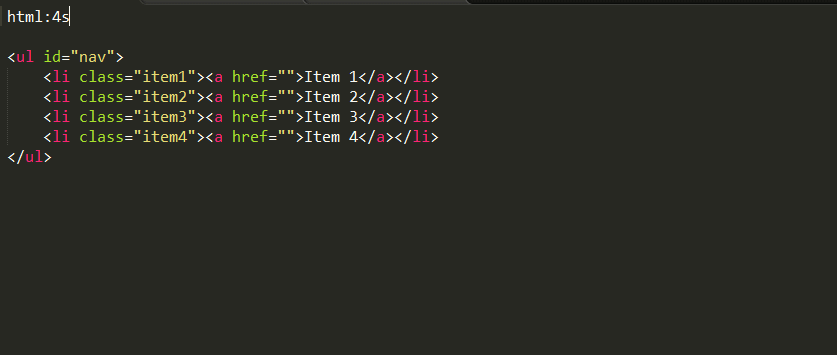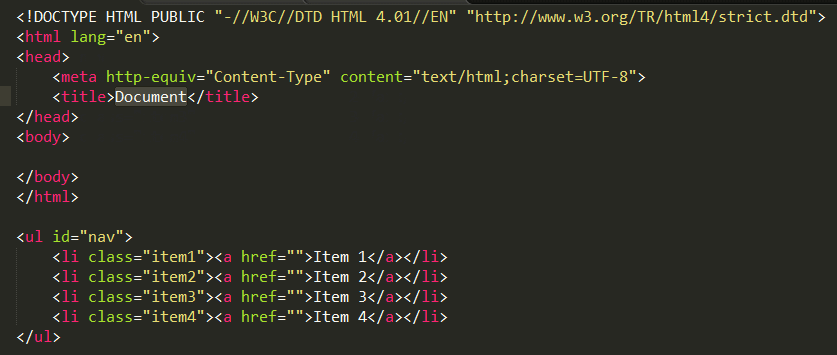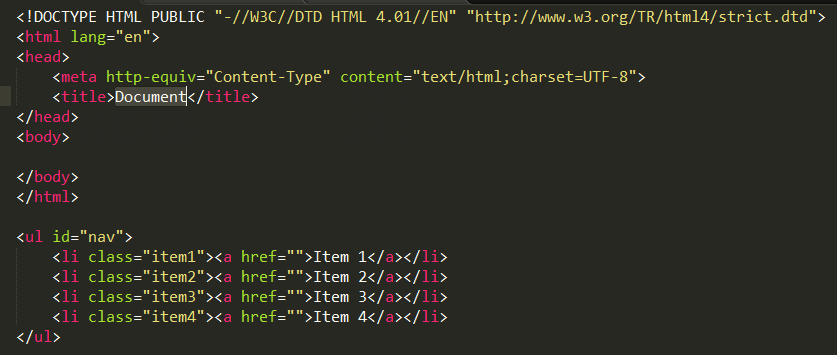
ul#test>li*4
按Ctrl+e 生成---
<ul id="test"><li></li><li></li><li></li><li></li> </ul>
JSFormat
功能:Javascript的代码格式化插件
简介:很多网站的JS代码都进行了压缩,一行式的甚至混淆压缩,这让我们看起来很吃力。而这个插件能帮我们把原始代码进行格式的整理,包括换行和缩进等等,是代码一目了然,更快读懂~
使用:在已压缩的JS文件中,右键选择jsFormat或者使用默认快捷键(Ctrl+Alt+F)