Sublime插件开发指引【教程导向】

article/2025/9/14 16:26:55

因为工作的原因，会接触到公司自己开发的自动化语言，但是这个语言从开发到现在，一直没有一个匹配的IDE（其实是有一个网页版的IDE，但是不好用没人用），而一直使用Notepad++，他们习惯了，但是我作为公司新人有点忍不了界面丑陋，没有高亮，不能快速折叠函数等等功能缺陷，所以自己看了看Sublime的插件指引，自己做了一个IDE适配自动化语言，特记录如何开发sublime插件。

文章介绍的并不全面，主要还是“领进门”，重在制作的方法。（因为自己也没有很懂😛）

插件支持的功能

  1. 自定义语言
  2. 主题（就是配色啥的）（该文章不介绍）
  3. 添加菜单
  4. 命令
  5. 自定义快捷键

命令/快捷键/菜单

这几个功能其实是相辅相成，共同使用的。

逻辑是：键盘按下一个组合件，触发命令，执行操作；或者在菜单中添加一个选项，点击这个选项来触发命令，执行操作。

我们先来一个简单的示例说明怎么做

示例1：添加一个上下文菜单，取名为“print hi”，当点击这个菜单时，在当前文件的起始位置打印hi

点击Tools -> Developer -> New Plugin
插入命令
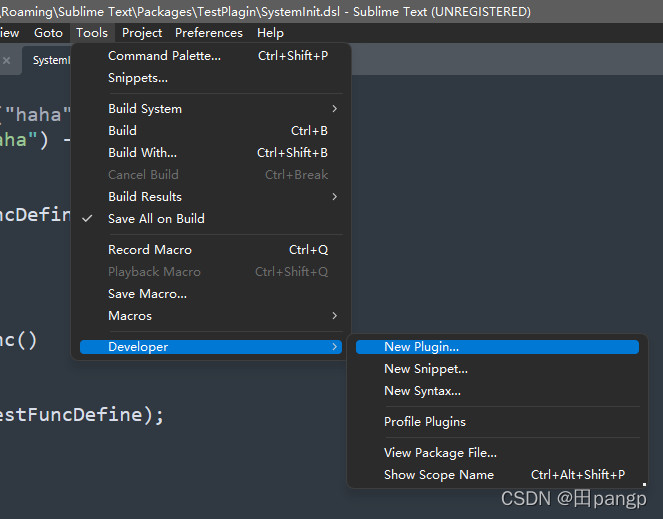
会新建一个python文件，并显示一个Demo

import sublime
import sublime_pluginclass ExampleCommand(sublime_plugin.TextCommand):def run(self, edit):self.view.insert(edit, 0, "Hello, World!")

可以看到这里有一个名为ExampleCommand类，重载了里面的run方法，方法中这个语句的含义是在文本的最开头位置插入"Hello World"文本，其中Command前面的Example就是命令的名称。

Command前面第一个大驼峰单词就是命令。比如PrintHiCommand这个类名，print就是命令的名称。命令这个概念我们后面就慢慢清楚了。

我们修改命令名为“printhi”，修改文本为"hi"。程序长这个样子：

import sublime
import sublime_pluginclass PrintHiCommand(sublime_plugin.TextCommand):def run(self, edit):self.view.insert(edit, 0, "hi")

ctrl+s保存一下，弹出保存对话框的路径自动就是插件所存在的地方，默认是**\Pakages\Users，所有的插件包都存放在Pakages文件夹下，你可以叫任意的名字。这里我们自己建立一个名为TestPackage的插件文件夹放置我们所有的插件文件。
路径

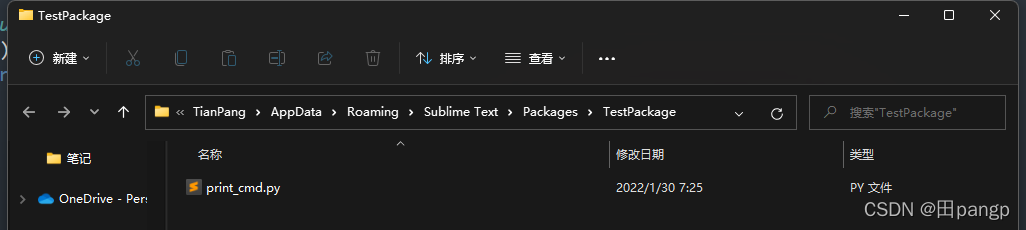
所有的插件包都存放在Pakages文件夹下
安装板sublime存放路径：
C:\Users[用户名]\AppData\Roaming\Sublime Text\Packages
绿色版sublime存放路径：
[sublime根目录]\Data\Packages\

这样我们第一个命令就做好了。

接下来，在这个文件夹下新建一个文件，取名为Context.sublime-menu，以json格式，写入以下内容

Context.sublime-menu。后缀表示该文件是定义菜单文件，Context文件名表示这个菜单将插入到上下文档中。

[{"caption": "hi","command": "print","id": "hi"}
]

caption表示菜单中的名称
command表示当选项被点击后，所触发的命令
id表示这个菜单项的唯一标识

保存文件，不用退出sublime，立刻可以看到效果。点击鼠标右键，看到最下面出现了名为hi的选项，点击可以看到文件的最前面输入了hi。
恭喜你，第一个插件已经完成了。

我用官方回答你的废话

开发插件怎么可能少了官方文档。
官方文档
上面就是sublime的文档地址。如果地址变动，也可以直接打开sublime官网官网地址，点击右上角Support，可以看到Documentation一栏，下面有很多指引，如直接打开documentation，或是官方论坛（不用翻墙可以访问），油管频道等。
我们重点介绍以下几个部分
在这里插入图片描述
有了前面的例子，相信大家已经知道如何编写插件，更多的功能自己看文档解决，毕竟我也没有精力写的很全。后文只会对文档中比较绕的名词和概念，以及我踩的坑做一说明。
那些英语不好的，右转各种翻译插件，谢谢。

菜单 Menu

  1. 只有caption和command是必要的，其他可写可不写。

  2. 其中mnemonic助记符，我也没有搞得很明白，如果有谁知道这个选项是干嘛的，烦请评论告诉大家，我会给你一个nubiplus。
    文档中只说了是一个按下一个按键可以激活进入入口，并且要和caption对应，也就是对应caption的第一个字母。我猜想是按下键盘的alt键，再组合按下这个助记符，可以激活指定的命令，就像直接鼠标点按菜单一样。

  3. Side Bar Mount Point.sublime-menu
    由于默认sublime隐藏侧边栏，我也是才知道这家伙还有个侧边栏。在View -> Side Bar -> Show Side Bar就可以显示侧边栏。
    上面的文件用于添加侧边栏顶部右键菜单。

    Tips
    在这里插入图片描述

  4. 可以带参

API

API Reference
python的文件名没有那么讲究，叫啥都行。

从前面的示例可以看到，我们自定义的类继承了sublime_plugin.TextCommand类。从官方的文档中也可以看到这个类的说明，我们重写了run()函数，当命令执行时，这个函数将会被调用，并执行里面的语句。

如果我们直接在函数中print()，打印的信息将会出现在哪里呢？
会在sublime的控制台当中。这一点非常重要，我们DEBUG经常会用到。使用快捷键ctrl+`，可以打开sublime的命令行。
此时，执行一下命令，可以看到输出。

import sublime
import sublime_pluginclass ExampleCommand(sublime_plugin.TextCommand):def run(self, edit):print("Hello World!")

在这里插入图片描述
下面会对部分类做一个简要说明：

  • sublime.View
    表示所打开文件的类。如在sublime中打开test.txt，那么view就代表这个test.txt对象。
    比如，关闭这个标签（其实也就是关闭这个文件）

    import sublime
import sublime_pluginclass ExampleCommand(sublime_plugin.TextCommand):def run(self, edit):self.view.close()

    从上面这个例子可以知道，sublime.View是sublime_plugin.TextCommand类的父类。
    view类还有很多函数，如sel()可以返回一段选中的范围、line()可以根据一个范围或点返回所在行，大家可以自己摸索。

  • sublime.Region
    表示一个范围。
    非常简单容易理解。注意，该类是可以直接根据头尾构造的。

  • sublime.Selection
    表示选中的对象。
    如果使用add()函数，将多个region添加进Selection对象中，就是多选。

自定义语言

我把这个放在了后面，主要是因为自定义语言这个功能应用场景应该比较少。
使用.sublime-syntax作为后缀名，对文件名没有要求，但是推荐以自定义的语言名作为名称。
该文件使用yaml语法，推荐先去熟悉一下什么是yaml语法。yaml语法
参考syntax官方说明文档
我们后文都以c语言做范例，先编写一个简单的Demo：

%YAML 1.2
---
name: C
file_extensions: [c, h]
scope: source.ccontexts:main:- match: \b(if|else|for|while)\bscope: keyword.control.c

name：语言名
file_extensions：所定义语言的拓展名
scope：应用范围（这个概念后面讲）
main：主上下文分支
match：匹配文本

原理

自定义语言最终的目的是解析语法，也就是让sublime根据文本特征，知道这段文字所表达的含义。
文本特征比如，c语言使用函数时，一定是函数名+括号的形式，根据这个特点，sublime就知道这里应该是一个函数，应该使用怎样的颜色高亮，除此之外，还可以知道这个函数的定义在哪。
我们在sublime-syntax文件中做的，就是定义文本特征，让sublime知道哪里是什么意思。
定义特征，使用的方法就是正则表达式，所以必须对正则非常熟悉。正则表达式

了解了上面的原理，我们需要对match和scope两个重要的概念做一个诠释。

  • match
    match是一个正则表达式，用于从文本开头到文本结束顺序的匹配文本规则。比如我们需要寻找括号前的英文识别为函数名，那么就需要编写正则
    - match: '\w(?=\()'
    match的单引号可以去掉，但是不能是双引号
    # 也可以这样
- match: \w(?=\()
  • scope
    当match匹配到了文本，scope就向sublime标识，这段文本是什么含义。
    - match: '\w(?=\()'scope: variable.function
    上面就表示所匹配到的文本，含义是函数变量。

有了上面基础还不够，还需要解决一个问题。类似函数体、函数当中的参数这样有“包裹结构”的，或者说层级结构的，如何表达。
比如，有下面一个例子。

int funcDemo(int a, int b)
{if (a == b){return a * 2;} else {return a + b;}
}

这里函数声明funcDemo，后面跟着形参，那么两个形参就是一个层级；再往后，是一对{}包裹的函数体，大括号中的所有内容都是属于funcDemo的函数体，那么函数体又是一个层级，依次向下推。。。
我们前面介绍过了，match是从前到后的匹配文本。那么文本就可以看作栈，当遇到funcDemo(第一个左括号时，可以看作是将后文的所有内容“进栈”，直到遇到了)右括号才将后文所有内容出栈，这样int a, int b就可以有办法表示为函数参数。函数体也同理；if、while等这样的语句也同理。
sublime中使用push和pop来进栈和出栈。

# 简单的函数定义规则
main:
- match: '(?<=\w+) *\('scope: punctuation.section.group.begin.cpush: function_paramterfunction_paramter:
- scope: meta.group.c- match: \b(int|float|double|char)\bscope: storage.type.c- match: \)scope: punctuation.section.group.end.cpop: true

从上面的示例可以看出，push可以将文本入栈到指定的yaml对象中解析，入栈的这一部分内容，会完全按照新的规则解析，直到遇到了pop，如果pop为true，则出栈到外面一层。
如果存在多层嵌套，就需要一层一层push再一层一层pop，直到根。这也符合c语言以及大多数语言的规定。
还有一个小细节非常值得注意，在function_paramter对象中，在第一个位置有十分孤单的scope并没有任何match与之对应scope: meta.group.c，其实这就是function_paramter的scope，表示这个对象的含义，一般以meta打头。

那么我们就明白了，最开始的示例中，最开头的scope，scope: source.c其实就是表示这个语言的根scope。

让我们开始吧！

懂得了上面的原理，做起来就非常轻松了。
官方文档中列举有几乎所有支持的scope定义scope naming文档

tips:
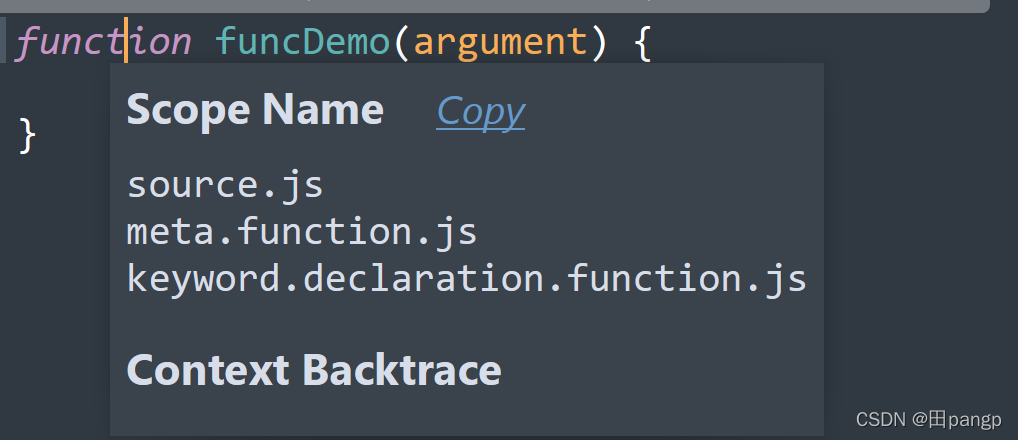
对于我们的自定义语言，最快速有效的开发方式就是对照别的语言来开发。使用快捷键ctrl+shift+alt+p快速查看文本定义。
比如对照着js语言，我们不知道function关键字会给一个怎样的scope，我们可以将光标移动到function上面，使用快捷键查看。
在这里插入图片描述
结合前文讲到的，scope是会根据不断的push、pop形成一个类似树状的结构，上面列出的就是按照从根到叶子的所有scope

除了刚刚介绍的push、pop以外，还有set可以直接把后文推到某个层级当中。
大致就是这样了，后面有哪里想起来需要添加的再添加进去。


http://chatgpt.dhexx.cn/article/nVB1oG6U.shtml

相关文章

专为前端开发者准备的 15 款优秀的 Sublime Text 插件

专为前端开发者准备的 15 款优秀的 Sublime Text 插件

作者 | IT程序狮链接 | https://www.jianshu.com/p/87fe1139f668 Sublime Text 已成为了目前最流行的代码编辑器之一。它的反应速度、简单易用性以及丰富的插件生态&#xff0c;让众多前端开发者们为之倾倒。 为了帮助开发者们更便捷地使用 Sublime Text &#xff0c;我们决定制…
阅读更多...
sublime上插件的安装与使用

sublime上插件的安装与使用

亲测可用&#xff0c;若有疑问请私信 1.插件安装的方式 插件安装方式一&#xff1a;直接安装 下载插件安装包后&#xff0c;把安装包解压到packages目录&#xff08;菜单->首选项->浏览插件目录&#xff09;中&#xff0c;完成安装 插件安装方法二&#xff1a;使用pac…
阅读更多...
K-means算法

K-means算法

目录 算法概述算法原理算法推导算法流程K值的确定 算法概述 K-means算法也称为K_均值算法&#xff0c;用于聚类算法。聚类是一种无监督学习&#xff0c;他将相似的对象归于一个簇中&#xff0c;簇中心通过簇中所有点的均值来计算。聚类算法与分类算法的主要区别就是分类的目标…
阅读更多...
Warshall 算法

Warshall 算法

Warshall算法 介绍&#xff1a; Warshall在1962年提出了一个求关系的传递闭包的有效算法。其具体过程如下&#xff1a; N—S图 代码实现&#xff1a; import java.util.Scanner;public class Warshall {public static void main(String[] args) {System.out.println("…
阅读更多...
基于BINN算法的CCPP全路径覆盖算法

基于BINN算法的CCPP全路径覆盖算法

1.CCPP整体算法文档 1.1 ccpp基础介绍 全路径覆盖算法&#xff08;CCPP: Complete Coverage Path Planning&#xff09;作为扫地机器人较为关键的组成部分&#xff0c;其问题的本质是&#xff1a;在栅格地图中,全覆盖路径规划问题就演变为寻找机器人的下一个移动位置,只有准确…
阅读更多...
差分进化算法

差分进化算法

文章目录 前言一、差分进化算法描述二、差分进化算法流程1.初始化2.变异3.交叉4.选择5。终结条件 2.流程图 总结 前言 差分进化算法(Differential Evolution Algorithm&#xff0c;DE)是一种高效的全局优化算法。它也是基于群体的启发式搜索算法&#xff0c;群中的每个个体对应…
阅读更多...
进化算法简单介绍

进化算法简单介绍

进化算法又称启发式算法&#xff0c;是利用经验法则或者常识来解决问题的方法。 图片来自参考文献&#xff08;1&#xff09;。 1. 元启发式算法和启发式算法有什么区别&#xff1f; 启发式策略&#xff08;heuristic&#xff09; 启发式算法(Heuristic Algorigthm)是一种基于…
阅读更多...
EM算法

EM算法

一、EM算法介绍 我们经常会从样本观察数据中&#xff0c;找出样本的模型参数。 最常用的方法就是极大化模型分布的对数似然函数。&#xff08;最大似然估计&#xff1a;利用已知的样本结果&#xff0c;反推最有可能导致这样结果的一组参数&#xff09;但是在一些情况下&#x…
阅读更多...
TDOA算法

TDOA算法

1.TDOA&#xff1a; TDOA&#xff1a;全称为Time Difference Of Arrival 到达时间差 距离差时间差*电磁波速度 TA-TBCONSTANT 2:TDOA定位基本原理 通过测量无线电信号到达不用监测地点的天线单元时间差&#xff0c;来对发射无线电信号的发射源进行定位 TDOA定位流程 从监测站将…
阅读更多...
SM2算法概述

SM2算法概述

2021SCSDUSC SM2算法概述 SM2椭圆曲线公钥密码算法是我国自主设计的公钥密码算法&#xff0c;包括SM2-1椭圆曲线数字签名算法&#xff0c;SM2-2椭圆曲线密钥交换协议&#xff0c;SM2-3椭圆曲线公钥加密算法&#xff0c;分别用于实现数字签名密钥协商和数据加密等功能。 SM2标…
阅读更多...
银行家算法

银行家算法

一 银行家算法作用&#xff1a; 动态防止进程死锁的算法 二 银行家算法步骤 第一步 判断是否存在一个安全序列&#xff0c;若存在一个安全序列则系统为安全的。 第二步1请求资源 判断 Request < Need Request < Available 第三步 假定可以分配资源 并修改 Availabl…
阅读更多...
Newton牛顿法（一）| 基本思想+迭代公式

Newton牛顿法（一）| 基本思想+迭代公式

基本思想与迭代公式 通常对已知方程 f ( x ) 0 f(x)0 f(x)0进行变形而构造的迭代函数 φ ( x ) \varphi(x) φ(x)不是惟一的。在实际作用中&#xff0c;如果希望迭代函数 φ ( x ) \varphi(x) φ(x)有一种固定格式的构造方法&#xff0c;就可以采用Newton迭代法。 Newton迭代…
阅读更多...
理解牛顿法

理解牛顿法

原创声明：本文为 SIGAI 原创文章，仅供个人学习使用，未经允许，不能用于商业目的。 其它机器学习、深度学习算法的全面系统讲解可以阅读《机器学习-原理、算法与应用》，清华大学出版社，雷明著，由SIGAI公众号作者倾力打造。 书的购买链接书的勘误，优化，源代码资源导言 …
阅读更多...
机器学习——牛顿法详解

机器学习——牛顿法详解

我们现在学习的机器学习算法&#xff0c;大部分算法的本质都是建立优化模型&#xff0c;通过特定的最优化算法对目标函数&#xff08;或损失函数&#xff09;进行优化&#xff0c;通过训练集和测试集选择出最好的模型&#xff0c;所以&#xff0c;选择合适的最优化算法是非常重…
阅读更多...
牛顿法的简单介绍及Matlab实现

牛顿法的简单介绍及Matlab实现

目录 牛顿法原理简介使用牛顿法求解一元方程使用牛顿法求解平面定位问题参考文献 牛顿法原理简介 牛顿法的原理是利用函数 f ( x ) f(x) f(x) 的泰勒级数的前几项来寻找方程 f ( x ) 0 f(x)0 f(x)0 的根。 f ( x ) f(x) f(x)在 x 0 x_0 x0​处的一阶泰勒展开 f ( x ) f ( x…
阅读更多...
牛顿法介绍

牛顿法介绍

目录 牛顿法介绍推导海森矩阵、泰勒公式、梯度下降法牛顿法特点 牛顿法介绍 首先牛顿法是求解函数值为0时的自变量取值的方法。如果你看不懂这句没关系&#xff0c;继续往下看就好。利用牛顿法求解目标函数的最小值其实是转化成求使目标函数的一阶导为0的参数值。这一转换的理…
阅读更多...
牛顿法，障碍法，内点法

牛顿法，障碍法，内点法

基于对数障碍函数法的内点法 牛顿法&#xff08;Newton Method&#xff09;对数障碍函数方法一个简单的例子python代码 牛顿法&#xff08;Newton Method&#xff09; 牛顿法与梯度下降法&#xff0c;最速下降法等优化算法类似&#xff0c;是基于梯度的方法。给定一个二次可微的…
阅读更多...
牛顿法python 实现

牛顿法python 实现

有用请点赞&#xff0c;没用请差评。 欢迎分享本文&#xff0c;转载请保留出处。 牛顿法也是求解无约束最优化问题的常用方法&#xff0c;有收敛速度快的优点。牛顿法是迭代算法&#xff0c;每一步需要求解目标函数的海赛矩阵的逆矩阵。同时还有拟牛顿法、阻尼牛顿法、修正牛顿…
阅读更多...
牛顿法及牛顿法求解优化问题

牛顿法及牛顿法求解优化问题

牛顿法及牛顿法求解优化问题 牛顿法 1. 由来和基本思想 牛顿法也叫牛顿迭代法和牛顿-拉夫森法 1. 牛顿迭代法&#xff1a;因为牛顿法的是通过迭代来实现的&#xff0c;每次运算都让结果比之前好一点。哪怕只好一点点&#xff0c;在很多次迭代之后也可以得到一个很好的结果甚…
阅读更多...
最优化-牛顿法（Newton）

最优化-牛顿法（Newton）

转&#xff1a;https://blog.csdn.net/qq_36330643/article/details/78003952 平时经常看到牛顿法怎样怎样&#xff0c;一直不得要领&#xff0c;今天下午查了一下维基百科&#xff0c;写写我的认识&#xff0c;很多地方是直观理解&#xff0c;并没有严谨的证明。在我看来&…
阅读更多...
推荐文章

Copyright @ 2022~2023