亲测可用,若有疑问请私信
1.插件安装的方式
插件安装方式一:直接安装
下载插件安装包后,把安装包解压到packages目录(菜单->首选项->浏览插件目录)中,完成安装
插件安装方法二:使用package control组件安装
2.Package control简介
Package contro是sublime软件的插件包管理器,通过该组件,我们可以很方便的管理我们插件(浏览,安装,卸载)
3.安装Package control(插件安装包管理器)
1.检查sublime是否安装了该组件 ctrl+shift+p 在命令板中输入PC,如下图表示没安装:

2.使用ctrl + ~调出sublime的命令行窗口(按esc关闭命令行窗口/控制面板):
3.找到安装package control命令代码,在控制台中运行:
Installation - Package Control
将对应的命令代码粘贴到控制台中,回车
4.若提示连接失败,表示安装失败:
5.重新输入命令运行,如果还是不行,换一种方式,ctrl+shift+p,在控制面板中输入install,点击install package control

等待一会,弹出下面的提示窗口,证明安装成功
6.点击确定,当控台输出以下提示时,表示安装成功:
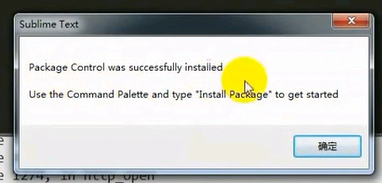
7.检测组件是否安装成功,以下界面是安装成功的状态:
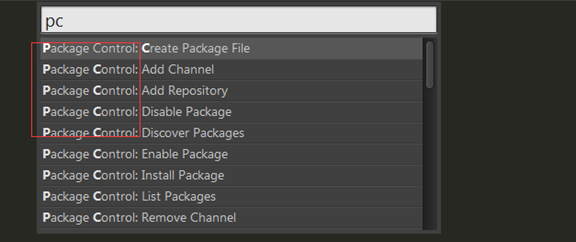
4.使用package control安装插件
1.ChineseLocalization汉化插件
--ctrl+shift+p
--在命令框中选中 package control:install package 选中它 按回车

左下角处等号开始左右摆动,加载插件列表
--加载完成,会弹出一个插件列表

--在命令框中输入 ChineseLocalization,选中插件,按回车
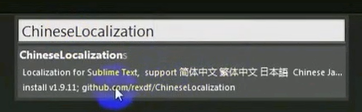
如果列表中没有,就手动下载,放到插件目录中
GitHub - rexdf/Chinese-Localization: 临时repo,请转到https://github.com/rexdf/ChineseLocalization
2. ConvertToUTF8
自动把文件编码方式转换为UTF-8
3.Emmet 能够快速编写HTML、CSS标记的插件

emmet插件使用:
可以快速生成一些其他代码
写好结构后,将光标放到语句最后,按tab键
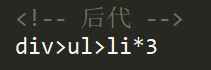



4. IMESupport 是用来支持输框跟随光标显示的插件(win7、win8、win10)
5. SublimeCodeIntel 代码提示插件,安装成功后会弹出一个文档
6. SidebarEnhancements 侧边栏插件,让侧边栏功能更丰富
7.FileHeader插件 可以自定义作者信息当前时间等信息,并将它们以注释的形式添加到文件的开头

5.删除插件
--ctrl+shift+p
--在命令框中选中 package control:remove package 选中它 按回车
--在命令框中输入 插件名称,选中插件,按回车