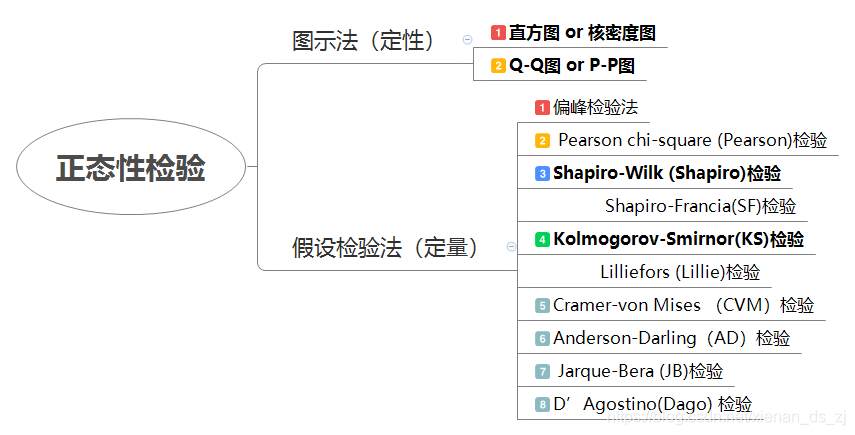
matlab 数据正态性检验

• matlab 数据正态性检验
  • 数据说明
  • 描述性图像
    • 指数走势图
    • 收益率散点图
    • 收益率频率分布直方图
  • Q-Q 图
  • 峰度与偏度系数
    • 峰度
    • 偏度
  • jb 检验
  • 代码下载

数据说明

以前推荐用tushare是因为tushare免费，但是现在tushare非常无耻，积分不透明变像收费早已背离初心，建议用其他数据平台。

我们想要对 2018年 深成指数日收益率正态性进行检验。首先我们从 tushare 中获取数据。tushare 是免费的数据源，如果你没有 tushare 账号，可以去这个网址注册个 https://tushare.pro/register?reg=126259 账号，好像直接点击链接会提示风险，需要复制打地址栏打开,然后获取自己的 token,替换到下文代码中 。然后需要把，tushare 官网的 matlab_tushare_sdk 放到我们的当前文件夹或者添加到 matlab 工作路径中。

数据获取部分的代码如下：

%% 从tushare中读取数据
% 加载tushare包
addpath(genpath(pwd));
% 此处换成你自己的token
token = '*********b937459c8b611e0a9***********';
api = pro_api(token);
start_time = '20180101';
end_time = '20181231';
ktype = 'D';index = pro_bar('399001.SZ', api, start_time, end_time,ktype,'I');

需要注意的是 tushare 中的数据日期顺序与 matlab 中的习惯不一致，因此需要翻转数据，即上面代码最后一行的操作。

描述性图像

指数走势图

我们用 18 年深成指数每日的收盘价绘制下图：

代码如下：

% 转换日期格式
temp = index.trade_date;
temp = char(temp);
temp = str2num(temp);
tradedate = datetime(temp,'ConvertFrom','yyyymmdd','format','yyyy-MM-dd');
% 绘制股价走势图
plot(tradedate,index.close)
title('深成指数走势图')
xlabel('时间');
ylabel('点数');
saveas(gcf,'深成指数走势图.jpg');

需要注意的是，此处我们先要将 tushare 中的时间，转换成 datetime 格式以便于绘图。

收益率散点图

求出深成指数每日的对数收益率，绘制下图：

代码如下：

% 计算收益率
ret = price2ret(index.close);
ret = [nan;ret];
% 保存原始数据
index.ret = ret;
writetable(index,'原始数据.xls');
% 绘制每日收益率图
figure;
plot(tradedate,ret,'*');
title('每日收益率图')
xlabel('时间');
ylabel('收益率');
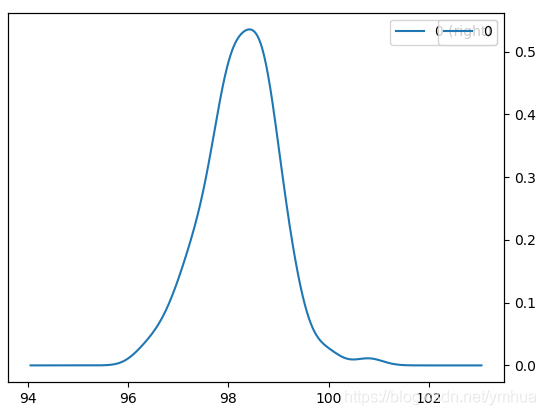
saveas(gcf,'深成指数每日收益率图.jpg');

收益率频率分布直方图

代码如下：

% 绘制收益率频率分布直方图
figure;
histogram(ret);
title('深成指数日收益率频率分布直方图');
xlabel('收益率');
ylabel('次数');
saveas(gcf,'深成指数日收益率频率分布直方图.jpg');

这边需要提醒的是，本文中所有绘制出来的图像，都通过 saveas 命令实现自动保存，这是非常实用的技巧。

Q-Q 图

其实，直方图已经让我们对深成指数收益率的分布有了直观的了解。接下来使用 qq 图进行进一步的描述。

QQ图通过把样本数据的分位数与已知分布相比较，从而来检验数据的分布情况。QQ图是一种散点图，正态分布的QQ图，就是由标准正态分布的分位数为横坐标，样本值为纵坐标的散点图。

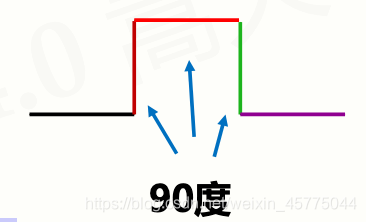
要利用QQ图鉴别样本数据是否近似于正态分布。图形是直线说明是正态分布。如果Q-Q图是直线，且该直线成45度角并穿过原点时，说明分布与给定的正态分布完全一样。如果是成45度角但不穿过原点，说明均值与给定的正态分布不同，如果是直线但不是45度角，说明均值与方差都与给定的分布不同。

图形中有一段是直线，在两端存在弧度，说明峰度的情况。如果Q-Q图中间部分是直线，但是右边在直线下面，左边在直线上面，说明分布的峰度小于零0，即轻尾。反之说明峰度大于0，即厚尾。而图形轻尾、厚尾形态分别如下：

至于图形的偏度情况，可以参看下图：

---

利用matlab的qqplot函数可以，绘制出下图：

代码如下：

%% qq
figure;
qqplot(ret);
saveas(gcf,'QQ图.jpg');

从绘制出来的图像可以看出，收益率的偏度不是非常明显。但是qq图左边明显向下偏，右边明显向上偏，说明存在尖峰厚尾的情况。

峰度与偏度系数

峰度

在进行了描述性分析后，为了得到更加客观的结果，我们可以求出收益率数据的偏度系数和峰度系数。

峰度是描述变量分布形态陡峭或平滑程度的统计量，通过对峰度系数的测量，我们能够判定数据相对于正态分布而言是更陡峭还是平缓。比如正态分布的峰度为0，均匀分布的峰度为-1.2（平缓），指数分布的峰度为6（陡峭）。

峰度，定义为四阶中心距。因为正态分布的峰度为3，因此在衡量分布是否是正态分布时会将峰度减3，计算公式为：

$$kurtosis=E[(\underset{\sigma }{}$$