文章目录
- 前言
- BPF-JITs中的bugs分类
- Subtle architectural semantics(微妙的架构语义)
- Subtle machine state(微妙的机器状态)
- Subtle instruction encoding(微妙的指令编码)
- Bug-fixing commits in BPF JITs in the Linux kernel (May 2014–April 2020)
- 其他
前言
本篇内容来自:Nelson L, Van Geffen J, Torlak E, et al. Specification and verification in the field: Applying formal methods to {BPF} just-in-time compilers in the Linux kernel[C]//14th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 20). 2020: 41-61.
这里记录论文3.2节 Bugs in BPF JITs 的阅读过程。
BPF-JITs中的bugs分类
我们手动审查了linux 内核,从2014年五月到2020年四月,所有关于BPF JITs的提交信息。我们对JIT目标为Arm32,Arm63,RV64,x86-32,x86-64的correctness bugs进行分类。correctness bugs指那些JIT生成错误指令的bugs,而非那些JIT过程中内存泄露等问题。下面描述了我们使用jitterbug发现的一些代表性的错误。
Subtle architectural semantics(微妙的架构语义)
RSH64_IMM是BPF中的逻辑右移指令。该指令根据立即数,将64位寄存器中的数值,进行逻辑右移。目标架构Arm32中的寄存器是32位的。所以JIT需要使用两个32位的寄存器来表示BPF指令中的64位寄存器。
下面的JIT代码逻辑为,使用两个32位寄存器,来表达一个64位寄存器的逻辑右移。
- 当右移位数小于32时:低位寄存器本身右移+接受高位移除的内容;高位寄存器直接右移。
- 当右移位数等于32时:使用高位寄存器的内容填充低位寄存器;高位寄存器清零。
- 当右移位数大于32时:高位寄存器移位后的内容填充低位寄存器;高位寄存器清零。
/* rd[0]: upper 32 bits of the destination register
rd[1]: lower 32 bits of the destination register
tmp2[1]: a temporary register */
if (val < 32) {
/* tmp2[1] = rd[1] >> val */
emit(ARM_MOV_SI(tmp2[1], rd[1], SRTYPE_LSR, val), ctx);
/* rd[1] = tmp2[1] | (rd[0] << (32 - val)) */
emit(ARM_ORR_SI(rd[1], tmp2[1], rd[0], SRTYPE_ASL,32 - val), ctx);
/* rd[0] = rd[0] >> val */
emit(ARM_MOV_SI(rd[0], rd[0], SRTYPE_LSR, val), ctx);
} else if (val == 32) {
/* rd[1] = rd[0] */
emit(ARM_MOV_R(rd[1], rd[0]), ctx);
/* rd[0] = 0 */
emit(ARM_MOV_I(rd[0], 0), ctx);
} else {
/* rd[1] = rd[0] >> (val - 32) */
emit(ARM_MOV_SI(rd[1], rd[0], SRTYPE_LSR,val - 32), ctx);
/* rd[0] = 0 */
emit(ARM_MOV_I(rd[0], 0), ctx);
}
代码逻辑很好,没问题。但是,对于Arm32而言,当逻辑右移的立即数为0时,表示逻辑右移32位。
BPF的RSH64_IMM指令,逻辑右移0位时,应当什么也没做。但按照上面的JIT代码指令,当翻译的指令在Arm32中执行时,会将寄存器清零。
修复这个问题也很容易,只需要在JIT时,当val为0时,什么也不做。
下面展示的是RV64 JIT的bug。
在RISC-V Reader Chiness的2.4节中,有这样一句话:
将 auipc 中的 20 位立即数与 jalr 中 12 位立即数的组合,我们可以将执行流转移到任何 32 位 PC 相对地址。
其JIT代码实现如下。
/* check if rvoff is in the range »−231,231 −1… */
if (!is_32b_int(rvoff))
return -ERANGE;
...
s64 upper = (rvoff + (1 << 11)) >> 12;
s64 lower = rvoff & 0xfff;
/* aupic t1,upper */
emit(rv_auipc(RV_REG_T1, upper), ctx);
/* jalr ra,lower(t1) */
emit(rv_jalr(RV_REG_RA, RV_REG_T1, lower), ctx);
但是,上面的JIT代码,在RV64中,无法实现转移到任何32位PC的相对地址。
因为,在RV64中,auipc和jalr使用的都是有符号数。这表示jalr中12位数的最高位为符号位。
所以在RV64中,能够转移的最大范围是:
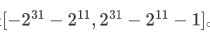
Subtle machine state(微妙的机器状态)
由于x86-32中寄存器数量的限制,JIT不得不将BPF寄存器入栈处理。
BPF中的JSET64_REG、JSET32_REG是两条跳转指令。JSET32_REG用C语言宏定义表示为 BPF_JMP[32]|BPF_JSET|BPF_X。
JSET64_REG DST,SRC,OFF的语义为jump if DST & SRC
x86-32中,对这两条指令的JIT编码如下。
- 如果是
JSET32_REG:将目标寄存器内容,从栈中提取放入eax中;将源寄存器内容,从栈中提取出来放入ecx中。 - 如果是
JSET64_REG:上面两步照做,分别存放的是源寄存器和目标寄存器的低32位。在使用两个寄存器edx,ebx分别存放源寄存器和目标寄存器的高32位。 - 将BPF的目标寄存器和源寄存器从栈中取出,放入机器真实的寄存器后,进行&操作。
- 根据&结果,修改标志zf位。跳转语句根据zf判断,是否跳转。
case BPF_JMP | BPF_JSET | BPF_X:
case BPF_JMP32 | BPF_JSET | BPF_X:
bool is_jmp64 = BPF_CLASS(insn->code) == BPF_JMP;
u8 dreg_lo = dstk ? IA32_EAX : dst_lo;
u8 dreg_hi = dstk ? IA32_EDX : dst_hi;
u8 sreg_lo = sstk ? IA32_ECX : src_lo;
u8 sreg_hi = sstk ? IA32_EBX : src_hi;
if (dstk) {EMIT3(0x8B, add_2reg(0x40, IA32_EBP, IA32_EAX),STACK_VAR(dst_lo)); /* eax <- dst_lo */if (is_jmp64)EMIT3(0x8B, add_2reg(0x40, IA32_EBP, IA32_EDX),STACK_VAR(dst_hi)); /* edx <- dst_hi */
}
if (sstk) {EMIT3(0x8B, add_2reg(0x40, IA32_EBP, IA32_ECX),STACK_VAR(src_lo)); /* ecx <- src_lo */if (is_jmp64)EMIT3(0x8B, add_2reg(0x40, IA32_EBP, IA32_EBX),STACK_VAR(src_hi)); /* ebx <- src_hi */
}
/* and dreg_lo,sreg_lo */
EMIT2(0x23, add_2reg(0xC0, sreg_lo, dreg_lo));
/* and dreg_hi,sreg_hi */
EMIT2(0x23, add_2reg(0xC0, sreg_hi, dreg_hi));
/* or dreg_lo,dreg_hi */
EMIT2(0x09, add_2reg(0xC0, dreg_lo, dreg_hi));
goto emit_cond_jmp; /* emit conditional jump */
上面JIT代码,当BPF指令为JSET64_REG,没有问题。
当时当BPF指令为JSET32_REG,有问题。因为,当指令为JSET32_REG时,不需要EMIT2(0x23, add_2reg(0xC0, sreg_hi, dreg_hi));和EMIT2(0x09, add_2reg(0xC0, dreg_lo, dreg_hi));。写代码的人估计是为了统一,让其存在,但,由于没有初始化寄存器edx、ebx为零,它们的操作会导致zf位再次被修改。
Subtle instruction encoding(微妙的指令编码)
论文中,想表达的意思是:JIT作为(BPF指令和实际机器指令)中间者,其想要生成的指令和实际生成指令,不等价。
论文举例是EMIT3(0xC7, add_1reg(0xC0, dst_hi), 0)生成的指令和mov dst_hi,0不等价。
这里是EMIT3的宏展开。我暂时没明白0xC7和0xC0是什么含义。不要紧,后期了解BPF-JIT之后,自然知道。
Bug-fixing commits in BPF JITs in the Linux kernel (May 2014–April 2020)
我这里粘贴下论文附录截图,详细见论文。
The following table lists bug-fixing commits in the BPF JITs in the Linux kernel for Arm32, Arm64, RV64, x86-32, and x86-64.
The superscripts 𝐽 and S mark those for fixing bugs found using Jitterbug and the BPF bug finder in Serval, respectively

其他
之前简单整理过ebpf指令系统,感兴趣的话,自行参考ebpf指令系统。