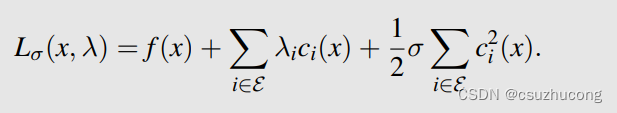拉格朗日函数优化

article/2025/9/20 0:00:17

等式约束最优化

可以写为：

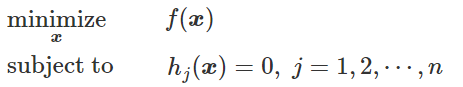
引入拉格朗日乘子（ $\lambda _i\ne 0$ ）把问题转换成拉格朗日函数

$L(x,\lambda)=\left[ f(x) +\sum_{i=1}^{n}\lambda_ih_i(x) \right]$

因为对于任何可行解，有 $h_i(x)=0$ ，所以有

$f(x)=L(x,\lambda )$ ，也就是， $minf(x)=minL(x,\lambda )$ 。

求解。对 $L(x,\lambda)$ 分别求 $x,\lambda$ 的偏导数为零，得到方程组求解极值点，然后从极值点挑出最值点。

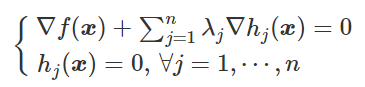
令 $x$ 的偏导为零，使得目标函数和约束函数的法向量共线（梯度共线）。为什么梯度共线能求到极值？

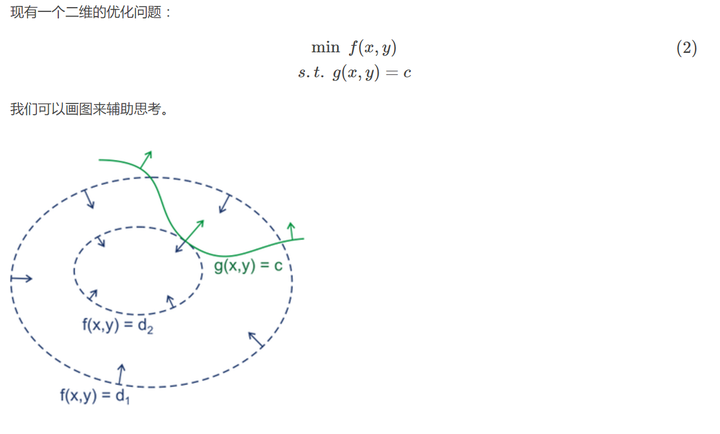
绿线标出的是约束 $g(x,y)=c$ 的点的轨迹。蓝线是 $f(x,y)$ 的等高线，箭头是各个点的梯度。

从图上可以看到，蓝线（ $f(x,y)=d_1$ ）与绿线相交，意味着肯定还存在其它的等高线（ $f(x,y)=d_2$ ）在该条等高线的内部或者外部，使得新的等高线与目标函数的交点的值更大或者更小。所以当取到极值时，蓝线与绿线相切，而切点的梯度共线。

不等式约束最优化

可以写为：

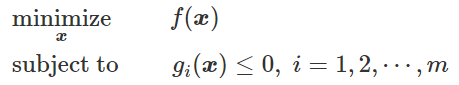
引入拉格朗日乘子（ $\mu _i\geq 0$ ），定义上述问题的拉格朗日量（Lagrangian）如下

$L(x,\mu )=\left[ f(x) +\sum_{i=1}^{m}\mu _ig_i(x) \right]$

同时定义拉格朗日对偶函数（Lagrange dual function）如下：

$F(\mu )=inf_x L(x,\mu )=inf_x \left[ f(x)+\sum_{i=1}^{m}\mu _ig_i(x) \right]$

一般情况下， $L(x,\mu )$ 是能取到最小值的，所以 $F(\mu )=inf_x L(x,\mu )=min_x L(x,\mu )$

求解。当强对偶性成立时，通过KKT条件求解极值点，然后从极值点挑出最值点。

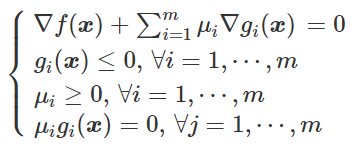
第一个条件使得目标函数和约束函数的法向量共线（梯度共线）。

最后一个条件称为互补松弛条件(Complementary Slackness Condition)。通过引入这个条件，增加了m个等式约束，使得等式的数量跟变量一样。

更一般地，我们把等式约束也加进来，优化问题可以写为：

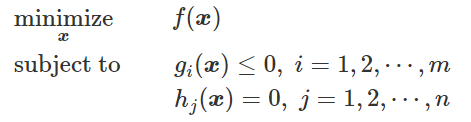
KKT条件为

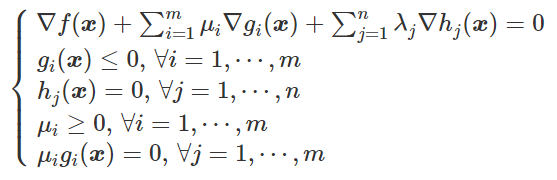
如果没有“不等式”约束条件，即 $m=0$ ，KKT条件就是拉格朗日乘数法中极值点满足的方程组。所以KKT条件是拉格朗日乘数法的推广，拉格朗日乘数法是KKT条件的特例。

注意到：

KKT条件是强对偶性的必要条件，强对偶性下KKT条件才成立
一般仅用KKT条件来验证找到的解
当目标函数和约束都是线性时，优化问题为我们熟悉的线性规划（LP）
在线性规划里， $\lambda ,\mu$ 表示的是对应约束的影子价格

4，KKT与强对偶性

这里讨论只有不等式约束，并且强对偶性的情况

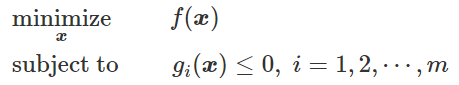
由强对偶性，有 $f(x)=max_\mu L(x,\mu )$ ，也就是， $min_xf(x)=min_x max_\mu L(x,\mu )$ 。

原问题目标函数为 $f(x)=max_\mu L(x,\mu )$ ，对应的对偶函数为 $F(\mu) =min_x L(x,\mu )$ 。

由强对偶性，我们有 $min_x f(x)= max_\mu F(\mu )$ ，也就是 $min_x max_\mu L(x,\mu ) = max_\mu min_x L(x,\mu )$

为什么强对偶下可以得到KKT条件？

首先看梯度共线。

用 $x^*$ 表示原问题取得最优值的解，也就是 $f(x^*)=min_x f(x)=min_x max_\mu L(x,\mu )$ 。由强对偶性，可得 $max_\mu min_x L(x,\mu )=min_x max_\mu L(x,\mu )=f(x^*)$ 。也就是说， $min_x L(x,\mu )$ 在 $x=x^*$ 处取得极值，也就是，偏导数为零。

然后看互补松弛条件。

当 $x=x^*$ 时，有 $max_\mu min_x L(x,\mu )=max_\mu\left[ f(x^*) +\sum_{i=1}^{m}\mu _ig_i(x^*) \right]=f(x^*)+max_\mu\left[ \sum_{i=1}^{m}\mu _ig_i(x^*) \right]=f(x^*)$ 。

也就是， $max_\mu\left[ \sum_{i=1}^{m}\mu _ig_i(x^*) \right]=0$ ，也就是 $\mu _ig_i(x^*)=0,\forall i=1,...,m$

5，拉格朗日函数与对偶性

对于不等式约束，

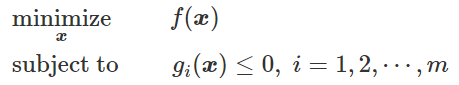
一般的，由 $\mu \geq 0,g_i(x)\leq 0$ ，有 $f(x)\geq max_\mu L(x,\mu )$ 。所以 $min_xf(x)\geq min_x max_\mu L(x,\mu )$ 。

而根据拉格朗日对偶函数，有对偶问题为 $max_\mu F(\mu )=max_\mu min_x L(x,\mu )$ 。由因为对偶问题是凸优化（Slater条件也满足），根据对偶问题的强对偶性，有 $max_\mu F(\mu )=max_\mu min_x L(x,\mu )= min_x max_\mu L(x,\mu )$ 。