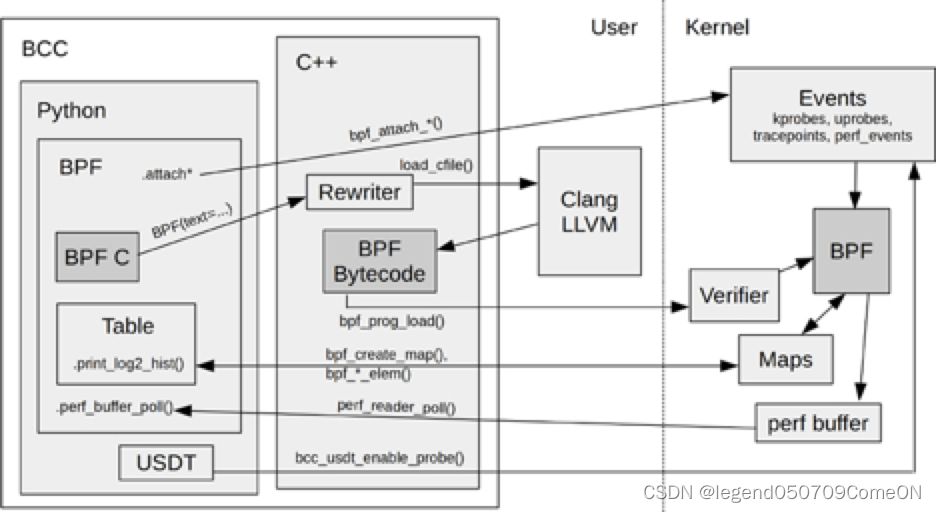
DPDK BPF

article/2025/9/19 23:19:46

DPDK BPF

DPDK 自版本 18.05 已集成了 librte_bpf, 主要利用rte_eth_rx_burst/rte_eth_tx_burst 回调函数机制, 执行eBPF字节码. 当前支持以下特性:

  • base eBPF ISA (except tail-pointer)
  • JIT (x86_64 and arm64 only)
  • eBPF code verifier
  • user-defined helper functions (64-bit only)
  • RX/TX filter (加载 eBPF grog 作为 DPDK RX/TX 回调函数处理数据包, 单独跟每个RX/TX绑定)
  • rte_mbuf access (64-bit only)

不支持的功能特性:

  • cBPF
  • eBPF MAP
  • tail-pointer calls
  • external function calls for 32-bit platforms

DPDK BPF 执行流程

在这里插入图片描述

Fedora

sudo dnf install -y git gcc ncurses-devel elfutils-libelf-devel bc \openssl-devel libcap-devel clang llvm graphviz bison flex glibc-static

generate bpf prog

examples/bpf/t1.c 提供了一个处理原始数据报文的例子, 检测到匹配IP地址与UDP目的端口5000则丢弃:

/* SPDX-License-Identifier: BSD-3-Clause* Copyright(c) 2018 Intel Corporation*//** eBPF program sample.* Accepts pointer to first segment packet data as an input parameter.* analog of tcpdump -s 1 -d 'dst 1.2.3.4 && udp && dst port 5000'* (000) ldh      [12]* (001) jeq      #0x800           jt 2    jf 12* (002) ld       [30]* (003) jeq      #0x1020304       jt 4    jf 12* (004) ldb      [23]* (005) jeq      #0x11            jt 6    jf 12* (006) ldh      [20]* (007) jset     #0x1fff          jt 12   jf 8* (008) ldxb     4*([14]&0xf)* (009) ldh      [x + 16]* (010) jeq      #0x1388          jt 11   jf 12* (011) ret      #1* (012) ret      #0** To compile on x86:* clang -O2 -U __GNUC__ -target bpf -c t1.c** To compile on ARM:* clang -O2 -I/usr/include/aarch64-linux-gnu/ -target bpf -c t1.c*/#include <stdint.h>
#include <net/ethernet.h>
#include <netinet/ip.h>
#include <netinet/udp.h>
#include <arpa/inet.h>uint64_t
entry(void *pkt)
{struct ether_header *ether_header = (void *)pkt;if (ether_header->ether_type != htons(0x0800))return 0;struct iphdr *iphdr = (void *)(ether_header + 1);if (iphdr->protocol != 17 || (iphdr->frag_off & 0x1ffff) != 0 ||iphdr->daddr != htonl(0x1020304))return 0;int hlen = iphdr->ihl * 4;struct udphdr *udphdr = (void *)iphdr + hlen;if (udphdr->dest != htons(5000))return 0;return 1;
}

编译bpf字节码:

# clang -O2 -U __GNUC__ -I${RTE_SDK}/${RTE_TARGET}/include -target bpf  -Wno-int-to-void-pointer-cast -c t1.c
# llvm-objdump  --arch=bpf -S t1.ot1.o:	file format elf64-bpfDisassembly of section .text:0000000000000000 <entry>:0:	b7 00 00 00 00 00 00 00	r0 = 01:	69 12 0c 00 00 00 00 00	r2 = *(u16 *)(r1 + 12)2:	55 02 0f 00 08 00 00 00	if r2 != 8 goto +15 <LBB0_6>3:	71 12 17 00 00 00 00 00	r2 = *(u8 *)(r1 + 23)4:	55 02 0d 00 11 00 00 00	if r2 != 17 goto +13 <LBB0_6>5:	69 12 14 00 00 00 00 00	r2 = *(u16 *)(r1 + 20)6:	55 02 0b 00 00 00 00 00	if r2 != 0 goto +11 <LBB0_6>7:	61 12 1e 00 00 00 00 00	r2 = *(u32 *)(r1 + 30)8:	55 02 09 00 01 02 03 04	if r2 != 67305985 goto +9 <LBB0_6>9:	07 01 00 00 0e 00 00 00	r1 += 1410:	71 12 00 00 00 00 00 00	r2 = *(u8 *)(r1 + 0)11:	67 02 00 00 02 00 00 00	r2 <<= 212:	57 02 00 00 3c 00 00 00	r2 &= 6013:	0f 21 00 00 00 00 00 00	r1 += r214:	69 11 02 00 00 00 00 00	r1 = *(u16 *)(r1 + 2)15:	b7 00 00 00 01 00 00 00	r0 = 116:	15 01 01 00 13 88 00 00	if r1 == 34835 goto +1 <LBB0_6>17:	b7 00 00 00 00 00 00 00	r0 = 00000000000000090 <LBB0_6>:18:	95 00 00 00 00 00 00 00	exit

load/unload bpf prog

testpmd 提供了一组bpf命令用于验证bpf功能:

testpmd> bpf-load rx|tx <portid> <queueid> <load-flags> <filename>
testpmd> bpf-unload rx|tx <portid> <queueid>

bpf with rte_mbuf*

bpf入参为 rte_mbuf *

bpf-load rx 0 0 M <path>/t3.o
...
bpf-load rx 0 n M <path>/t3.o

bpf with raw packet

bpf入参为原始报文数据

bpf-load rx 0 0 J <path>/t4.o
...
bpf-load rx 0 n J <path>/t4.o

bpf with vm

bpf入参为原始报文数据, 使用 bpf vm 执行字节码:

bpf-load rx 0 0 - <path>/t5.o
...
bpf-load rx 0 n - <path>/t5.o

unload bpf

bpf-unload rx 0 0
...
bpf-unload rx 0 n

Performance

硬件

CPU: Intel(R) Xeon(R) Platinum 9242 CPU @ 2.30GHz
Mellanox Technologies MT2892 Family [ConnectX-6 Dx]

dpdk 21.05 testpmd:

!/bin/sh#EAL_ARGS+=" --log-level="lib.eal":8 --log-level=pmd:8 --log-level="pmd.net.mlx5":3 "
NR_Q=18APP=./dpdk-testpmd-21.05
$APP -l 24-47 --socket-mem=4096,4096 -n 4  -w '54:00.1,dv_flow_en=1,mprq_en=1,rxqs_min_mprq=1,rx_vec_en=1' ${EAL_ARGS}  -- \-i  --rxq=${NR_Q} --txq=${NR_Q} --nb-cores=23 --forward-mode icmpecho --no-numa --enable-rx-cksum --auto-start --rxd=2048 --txd=2048 --burst=64

bpf prog

bpf 丢弃UDP目的端口为5000所有数据报文: t1.c 简化版, 移除了IP地址判断:

#include <stdint.h>
#include <net/ethernet.h>
#include <netinet/ip.h>
#include <netinet/udp.h>
#include <arpa/inet.h>uint64_t
entry(void *pkt)
{struct ether_header *ether_header = (void *)pkt;if (ether_header->ether_type != htons(0x0800))return 1;struct iphdr *iphdr = (void *)(ether_header + 1);if (iphdr->protocol != 17)return 1;int hlen = iphdr->ihl * 4;struct udphdr *udphdr = (void *)iphdr + hlen;if (udphdr->dest != htons(5000))return 0;return 0;
}

编译:

clang -O2 -U __GNUC__ -I${RTE_SDK}/${RTE_TARGET}/include -target bpf  -Wno-int-to-void-pointer-cast -c t4.c

Load:

bpf-load rx 0 0 J <path>/t4.o
bpf-load rx 0 1 J <path>/t4.o
bpf-load rx 0 2 J <path>/t4.o
bpf-load rx 0 3 J <path>/t4.o
bpf-load rx 0 4 J <path>/t4.o
bpf-load rx 0 5 J <path>/t4.o
bpf-load rx 0 6 J <path>/t4.o
bpf-load rx 0 7 J <path>/t4.o
bpf-load rx 0 8 J <path>/t4.o
bpf-load rx 0 9 J <path>/t4.o
bpf-load rx 0 10 J <path>/t4.o
bpf-load rx 0 11 J <path>/t4.o
bpf-load rx 0 12 J <path>/t4.o
bpf-load rx 0 13 J <path>/t4.o
bpf-load rx 0 14 J <path>/t4.o
bpf-load rx 0 15 J <path>/t4.o
bpf-load rx 0 16 J <path>/t4.o
bpf-load rx 0 17 J <path>/t4.o

result

在当前测试硬件环境下, icmpecho 为 RX-DROP处理模式, 执行bpf字节码只做简单丢弃, 这种方式对性能几乎无影响, 可考虑用于插件处理数据包:

testpmd> show port stats all######################## NIC statistics for port 0  ########################RX-packets: 81360790320 RX-missed: 8141       RX-bytes:  4881647419320RX-errors: 0RX-nombuf:  0         TX-packets: 4          TX-errors: 0          TX-bytes:  360Throughput (since last show)Rx-pps:    149155140          Rx-bps:  71594467312Tx-pps:            0          Tx-bps:            0############################################################################bpf-unload rx 0 0
bpf-unload rx 0 1
bpf-unload rx 0 2
bpf-unload rx 0 3
bpf-unload rx 0 4
bpf-unload rx 0 5
bpf-unload rx 0 6
bpf-unload rx 0 7
bpf-unload rx 0 8
bpf-unload rx 0 9
bpf-unload rx 0 10
bpf-unload rx 0 11
bpf-unload rx 0 12
bpf-unload rx 0 13
bpf-unload rx 0 14
bpf-unload rx 0 15
bpf-unload rx 0 16
bpf-unload rx 0 17
testpmd> show port stats all######################## NIC statistics for port 0  ########################RX-packets: 60151600493 RX-missed: 8141       RX-bytes:  3609096029700RX-errors: 0RX-nombuf:  0         TX-packets: 4          TX-errors: 0          TX-bytes:  360Throughput (since last show)Rx-pps:    149159900          Rx-bps:  71596752112Tx-pps:            0          Tx-bps:            0############################################################################
testpmd>

Reference

eBPF spec
DPDK- Berkeley Packet Filter Library
Awesome eBPF
Cilium - BPF and XDP Reference Guide


http://chatgpt.dhexx.cn/article/pT4dvaBD.shtml

相关文章

Linux超能力BPF技术介绍及学习分享

Linux超能力BPF技术介绍及学习分享

近两年BPF技术跃然成为了一项热门技术&#xff0c;在刚刚结束的KubeCon 2020 Europe会议上有7个关于BPF的技术分享&#xff0c; 而在KubeCon 2020 China会议上也已有了3个关于BPF技术的中文分享&#xff0c;分别来自腾讯和PingCAP&#xff0c;涉足网络优化和系统追踪等领域。在…
阅读更多...
bpf原理与入门

bpf原理与入门

一、bpf架构 如上图所示，bpf由六部分构成，以下为其在bpf中的作用： bpf工具：该部分涉及bpf用户态程序、bpf的编译工具，通过bpf编译工具如Clang、LLVM将bpf用户态程序编译成bpf字节码； 加载器：可以简单理解为bpf系统调用，将bpf字节码加载到内核； 验证器：对bpf程序的…
阅读更多...
BPF入门1：BPF技术简介

BPF入门1：BPF技术简介

目录 cbpf 介绍ebpf 介绍ebpf 和 cbpf对比ebpf和内核模块的对比 ebpf应用ebpf架构Why BPF is FAST指令虚拟机JIT How BPF extends KernelLLVM 编写ebpf程序BCCBPFTraceC 语言原生方式 国内大厂使用ebpf的实践经验参考 cbpf 介绍 BPF&#xff08;Berkeley Packet Filter &#…
阅读更多...
增广拉格朗日函数

增广拉格朗日函数

对于优化问题 arg ⁡ min ⁡ z E ( z ) ( 1 a ) s . t . C z − b 0 ( 1 b ) \mathop{\arg\min}_{z} \ E(z)\qquad(1a)\\ s.t. \quad Cz-b0 \qquad(1b) argminz​ E(z)(1a)s.t.Cz−b0(1b) 其增广拉格朗日函数被定义为&#xff1a; L ( z , α , μ ) E ( z ) α T ( C z −…
阅读更多...
约束优化：PHR-ALM 增广拉格朗日函数法

约束优化：PHR-ALM 增广拉格朗日函数法

文章目录 约束优化&#xff1a;PHR-ALM 增广拉格朗日函数法等式约束非凸优化问题的PHR-ALM不等式约束非凸优化问题的PHR-ALM对于一般非凸优化问题的PHR-ALM参考文献 约束优化&#xff1a;PHR-ALM 增广拉格朗日函数法 基础预备&#xff1a; 约束优化&#xff1a;约束优化的三种…
阅读更多...
matlab编写拉格朗日插值代码函数

matlab编写拉格朗日插值代码函数

要求&#xff1a;根据拉格朗日多项式插值法原理&#xff0c;设计算法流程并且编写拉格朗日插值代码函数。 代码如下&#xff1a; function[y]lagrange(x0,y0,x) %建立一个函数名为lagrange的函数&#xff0c;输入x0,y0为插值点的坐标&#xff0c;均为数组&#xff0c;x为要…
阅读更多...
拉格朗日函数最优化问题

拉格朗日函数最优化问题

目的&#xff1a;将有约束条件的函数最优化问题通过拉格朗日函数转化为无条件的函数最优化问题。 条件极值最优化问题&#xff1a; 对于无条件的函数最优化问题&#xff0c;常用的有3种方式&#xff1a; 梯度下降&#xff1a;求解一阶导数&#xff0c;其实就是使用泰勒一阶展…
阅读更多...
【深度学习】拉格朗日（ Lagrange）中值定理

【深度学习】拉格朗日（ Lagrange）中值定理

文章目录 1、定理2、几何意义3、证明思路4、有限增量定理5、推论1、定理 如果函数 f(x) 满足： 在闭区间[a,b]上连续； 在开区间(a,b)内可导。 那么在(a,b)内至少有一点ξ(a<ξ<b)，使等式 ： f(b)-f(a)=f′(ξ)(b-a) 成立，或： f′(ξ) =(f(b)-f(a)) / (b-a) 或存…
阅读更多...
拉格朗日（lagrange)插值及其MATLAB程序

拉格朗日（lagrange)插值及其MATLAB程序

一、n次拉格朗日插值 根据《插值多项式的性质》中的定理6.1可得 其中&#xff08;6.19&#xff09;称为基函数&#xff0c;&#xff08;6.18&#xff09;称为拉格朗日多项式&#xff0c;用&#xff08;6.18&#xff09;计算插值称为拉格朗日多项式插值。 方法2&#xff1a;通过…
阅读更多...
拉格朗日函数优化

拉格朗日函数优化

等式约束最优化 可以写为&#xff1a; 引入拉格朗日乘子&#xff08;&#xff09;把问题转换成拉格朗日函数 因为对于任何可行解&#xff0c;有&#xff0c;所以有 &#xff0c;也就是&#xff0c;。 求解。对分别求的偏导数为零&#xff0c;得到方程组求解极值点&#xff0c…
阅读更多...
增广拉格朗日函数法

增广拉格朗日函数法

增广拉格朗日函数法 在二次罚函数法中&#xff0c;为了保证可行性&#xff0c;罚因子必须趋于正无穷。此时&#xff0c;子问题因条件数爆炸而难以求解。那么&#xff0c;是否可以通过对二次罚函数进行某种修正&#xff0c;使得对有限的罚因子&#xff0c;得到的毕竟最优解也是…
阅读更多...
增广拉格朗日函数法（ALM）

增广拉格朗日函数法（ALM）

增广拉格朗日函数法&#xff08; Augmented Lagrangian method&#xff09; 一、等式约束 考虑问题&#xff1a; min ⁡ x f ( x ) s . t . c i ( x ) 0 , i 1 , ⋯ , m . \begin{array}{ll} \min_x &f(x)\\ s.t. &c_i(x) 0, \quad i1,\cdots,m. \end{array} min…
阅读更多...
广义拉格朗日函数的理解

广义拉格朗日函数的理解

1、拉格朗日函数&#xff1a; 求极值 求函数f(x,y,z)在条件φ(x,y,z)0下的极值 方法&#xff08;步骤&#xff09;是&#xff1a; 1.做拉格朗日函数Lf(x,y,z)λφ(x,y,z),λ称拉格朗日乘数 2.求L分别对x,y,z,λ求偏导,得方程组,求出驻点P(x,y,z) 如果这个实际问题的最大或…
阅读更多...
各种拉格朗日函数

各种拉格朗日函数

目录 一&#xff0c;拉格朗日函数 二&#xff0c;部分拉格朗日函数 三&#xff0c;增广拉格朗日函数 一&#xff0c;拉格朗日函数 以三元函数为例&#xff1a; 求f(x,y,z)的极值&#xff0c;s.t.g(x,y,z)0 拉格朗日函数L(x,y,z,a) f(x,y,z) a * g(x,y,z) 在极值点处一…
阅读更多...
拉格朗日函数相关推导

拉格朗日函数相关推导

优化问题&#xff08;即高数中的求极值&#xff09;可分为三类&#xff1a;无约束、等式约束、不等式约束。 对于无约束的优化问题&#xff1a;求导&#xff0c;令导数为零即可求解。 等式约束优化&#xff1a;&#xff08;拉格朗日乘子法最开始就是求解等式约束优化的方法&…
阅读更多...
HJ-浇花

HJ-浇花

链接&#xff1a;https://ac.nowcoder.com/acm/contest/322/M 来源&#xff1a;牛客网 时间限制&#xff1a;C/C 1秒&#xff0c;其他语言2秒 空间限制&#xff1a;C/C 32768K&#xff0c;其他语言65536K 64bit IO Format: %lld 题目描述 HJ养了很多花&#xff08;9999999…
阅读更多...
单片机——自动浇花系统

单片机——自动浇花系统

目录 1、图片 2、代码 1、图片 2、代码 #include <reg51.h> //调用单片机头文件 #define uchar unsigned char //无符号字符型 宏定义 变量范围0~255 #define uint unsigned int //无符号整型 宏定义 变量范围0~65535#include <intrins.h>sbi…
阅读更多...
基于ESP32的开源定时浇花系统

基于ESP32的开源定时浇花系统

基于ESP32的开源定时浇花系统 文章目录 基于ESP32的开源定时浇花系统前言一、软硬件环境二、模块连接图1.浇花功能说明2.Web界面展示 总结 前言 养了些许花花草草&#xff0c;需要按时浇灌&#xff0c;奈何总是要出差&#xff08;总想出去玩&#xff09;&#xff0c;又怕没人浇…
阅读更多...
RISC-V MCU 自动浇花装置设计

RISC-V MCU 自动浇花装置设计

第一部分 设计概述 1.设计目的 在家里养养盆花可以陶冶情操&#xff0c;丰富生活&#xff0c;因此&#xff0c;家庭盆栽如今被许多人喜爱。花草生长问题80%以上是由花儿浇灌问题引起的;好不容易种植几个月的花草&#xff0c;因为浇水不及时而缺水死亡。虽然市场上有卖盆花自…
阅读更多...
【Proteus仿真】【51单片机】自动浇花灌溉系统设计

【Proteus仿真】【51单片机】自动浇花灌溉系统设计

文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用Proteus8仿真51单片机控制器&#xff0c;使用LCD1602液晶、按键、DS18B20、PCF8591 ADC、土壤湿度传感器、水位传感器、蜂鸣器模块等。 系统运行后&#xff0c;LCD1602显示传感器检测的温度、…
阅读更多...
推荐文章

Copyright @ 2022~2023