前言

来源：Linux Observability with BPF

这里整理下该书第一章：preface && Introduction

这本书有中文版的《Linux内核观测技术BPF》。这个链接里面的资料也是很好的，可以参考。

在开始看书之前，我们不妨先刷下相关视频，有个大概了解：高效入门eBPF – Linux内核之旅 – bilibili | BPF C编程入门 – Linux内核之旅 – bilibili | Linux 核心設計 透過 eBPF 觀察作業系統行為 – 黃敬群老师 – 成功资大

我之前整理数据包嗅探原理介绍的时候，简单查过bpf，当时没看懂。冤家路窄，今天又遇到了，哈哈哈。

看完上面三个链接视频，书上第一章Introduction快速翻下就好。这里简单整理下，下面只有干巴巴的文字，无任何图片。

当然也可以参考这：bpf_intro

preface

这本书的目的是帮助您熟悉在使用该Linux子系统的日常工作中需要的基本BPF概念。 BPF仍是一种发展中的技术，在我们编写本书时，新的概念和范例也在不断发展。 理想情况下，这本书将为您提供BPF基础组件的坚实基础，从而帮助您轻松地扩展知识。[这本书可能更多的是应用；原理介绍可能较少；所以可能难度上也简单些，不放刷快些。]

阅读了许多这些资源后，我们意识到每次需要学习有关BPF的知识时，我们都需要在许多博客文章，手册页以及Internet上的其他地方之间切换。 这本书是我们试图将分散在网络上的知识集中放置在中心位置，以供下一代BPF发烧友学习这一奇妙技术的方法。

这本书可以帮助您完成工作。 通常，如果本书提供了示例代码，则可以在程序和文档中使用它。 除非您复制了很大一部分代码，否则无需与我们联系以获取许可。 例如，编写使用本书中若干代码段的程序无需许可。 出售或分发O’Reilly书籍中的示例确实需要获得许可。 引用本书并引用示例代码来回答问题无需许可。 将本书中的大量示例代码合并到您的产品文档中确实需要获得许可。如果您认为对代码示例的使用超出了合理使用范围或此处给出的许可范围，请随时通过permissions@oreilly.com与我们联系。

Introduction

日志可以提供程序行为方式的精确数据。但是，日志只能提供，该程序构造者暴露出来的信息。通过日志推出程序执行流程具有挑战性。而黑天鹅事件，在软件工程中常常发生。可观察性可以帮助我们构建强壮的系统。

打开文件是一种事件，由CPU执行任意指令是一个事件，接收网络数据包是一个事件。BPF允许您编写在内核触发任何事件时可以安全执行的程序。 BPF为您提供了强有力的安全保证，以防止您在这些程序中注入系统崩溃和恶意行为。 BPF一系列程序工具，可以帮助系统开发人员观察和使用这些新平台。

历史发展

1992年，Steven McCanne和Van Jacobson撰写了论文The BSD Packet Filter:A New Architecture for User-Level Packet Capture。 在论文中，作者描述了他们如何为Unix内核实现网络数据包过滤器，该速度比当时的数据包过滤技术快20倍。 数据包过滤器有一个特定的目的：提供一个应用程序，该程序使用内核中的直接信息来监视系统网络的。 利用这些信息，应用程序可以决定如何处理这些数据包。 BPF在数据包过滤方面引入了两项重大创新:

• 一种新的虚拟机（VM），旨在与基于寄存器的CPU有效地协同工作。
• 每个应用程序缓冲区的使用可以过滤数据包而不复制所有数据包信息。 这样可以最大程度地减少决策所需的数据BPF。

2014年初，Alexei Starovoitov引入了扩展的BPF实施。 这项新设计针对现代硬件进行了优化，使其生成的指令集比旧的BPF解释器生成的机器代码更快。 此扩展版本还将BPF VM中的寄存器数量从2个32位寄存器增加到10个64位寄存器。 寄存器数量及其宽度的增加为编写更复杂的程序提供了可能，因为开发人员可以使用函数参数自由地交换更多的信息。 这些更改以及其他改进使扩展的BPF版本的速度比原始BPF实施快了四倍。

2014年6月，BPF的扩展版本暴露于用户空间。 这是BPF未来的拐点。正如Alexei在介绍这些更改的补丁中所写的那样，此补丁集展示了eBPF的潜力。

BPF成为顶级内核子系统，并且不再局限于网络堆栈。 BPF程序开始看起来更像内核模块，重点是安全性和稳定性。 与内核模块不同，BPF程序不需要您重新编译内核，并且可以确保它们完成而不会崩溃。

我们将在下一章中讨论的BPF验证器添加了这些必需的安全保证。 这样可以确保所有BPF程序都能正常运行而不会崩溃，并且可以确保程序不会尝试访问超出范围的内存。 但是，这些优点带有一定的限制：程序具有最大允许的大小，并且需要对循环进行限制，以确保不良BPF程序不会耗尽系统的内存。

通过更改使BPF可从用户空间访问，内核开发人员还添加了一个新的系统调用（syscall），bpf。 这个新的系统调用将成为用户空间和内核之间的核心通信。后面会介绍，syscall与BPF程序和maps一起使用。BPF maps将成为在内核和用户空间之间交换数据的主要机制。

结构

BPF内核中的体系结构令人着迷。 在整本书中，我们将深入探讨其具体细节，但在本章中，我们希望为您提供有关其工作原理的快速概述。

如前所述，BPF是一种高级虚拟机，在隔离的环境中运行代码指令。 从某种意义上讲，您可以像对Java虚拟机（Java Virtual Machine，JVM）那样思考BPF。Java虚拟机是run从高级编程语言编译而来的机器代码的专用程序。 编译代码后，BPF使用验证程序来确保该程序可以安全地由内核运行。 它可以防止您运行可能会使内核崩溃而危及系统的代码。 如果您的代码安全，则BPF程序将被加载到内核中。 Linux内核还为BPF指令集成了即时（JIT）编译器。 程序经过验证后，JIT将直接将BPF字节码转换为机器码，从而避免了执行时间的开销。

在内核运行任何BPF程序之前，它需要知道该程序附加到哪个执行点。 内核中有多个连接点，并且列表在不断增加。 执行点由BPF程序类型定义； 我们将在下一章中讨论它们。 选择执行点时，内核还会提供特定的函数帮助器，可用于处理程序接收的数据，从而使执行点和BPF程序紧密耦合。

BPF体系结构的最后一个组件负责在内核和用户空间之间共享数据。 该组件称为BPF maps，我们将在第3章中讨论映射。BPF映射是共享数据的双向结构。 这意味着您可以从内核和用户空间这两个方面进行写入和读取。 有几种类型的结构，从简单的数组和哈希图到专用的图，可以将整个BPF程序保存在其中。

推荐阅读

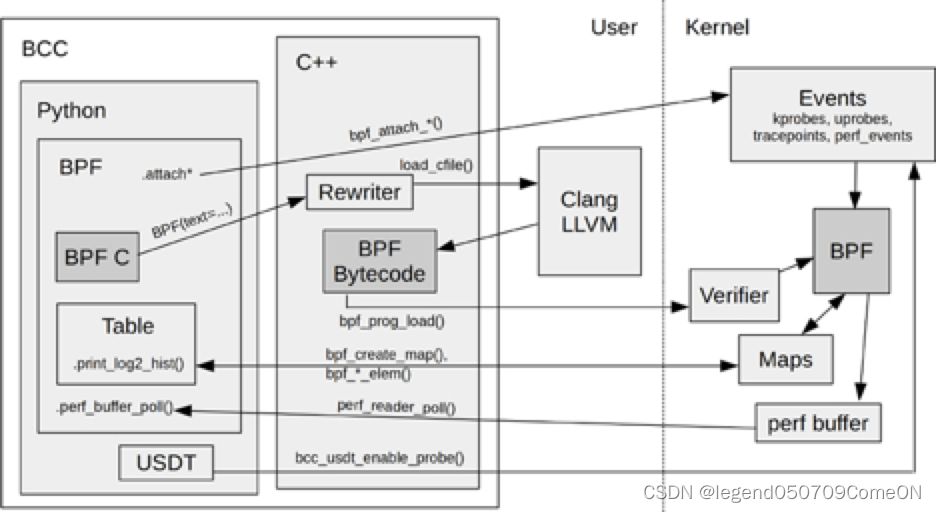
EBPF文章翻译(1)—EBPF介绍
下面这张图片，也来自该链接。