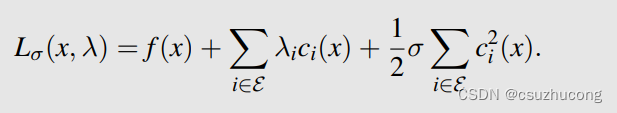约束优化：PHR-ALM 增广拉格朗日函数法

基础预备：

约束优化：约束优化的三种序列无约束优化方法

凸优化学习笔记：Lagrange函数、对偶函数、对偶问题、KKT条件

由前面的分析我们已经知道，在约束优化的三种序列无约束优化方法中，罚函数法存在Hessian矩阵条件数爆炸而难以求解的问题，Uzawa’s Method要求原目标函数必须为连续凸，这些都对适用范围存在严苛限制。增广拉格朗日函数法对原问题的凸性不做要求，并可以通过对二次罚函数进行某种修正，使得对有限的罚因子，得到的逼近最优解也是可行的。

等式约束非凸优化问题的PHR-ALM

从前面文章中的分析可知，不管原问题是不是凸优化问题，原问题的对偶问题一定是凸优化问题，这是因为对偶问题极大化的目标函数是凹函数，且约束集合为凸集，这是一个非常重要且有用的性质。如下图所示，在Uzawa’s method中，优化问题$d(\lambda ):={\min }_{x}f(x)+{\lambda }^{\mathrm{T}}h(x)，s.t.\lambda \le 0$非凸，因为函数$f(x)+{\lambda }^{\mathrm{T}}h(x)$非凸，则无法求出唯一的最优$x$带入下一步的$\lambda$更新计算。

已知${\max }_{\lambda }f(x)+{\lambda }^{\mathrm{T}}h(x)=\{\begin{array}{l}f(x),h(x)=0\\ \infty ,\text{ otherwise }\end{array}$是一个不连续函数，如何处理这个不连续的函数，一个非常直观的方法就是将该问题近似成一个连续问题，这是PHR方法的基本思想。增加一项$-\frac{1}{2\rho }\Vert \lambda -\bar{\lambda }{\Vert }^2$，用来近似平滑原来不连续的函数${\max }_{\lambda }f(x)+{\lambda }^{\mathrm{T}}h(x)$，其中$\rho >0$用来惩罚$\lambda$与先验值$\bar{\lambda }$之间的偏差。

这样一来，函数$f(x)+{\lambda }^{\mathrm{T}}h(x)-\frac{1}{2\rho }\Vert \lambda -\bar{\lambda }{\Vert }^2$被近似成一个光滑函数，同时$f(x)+{\lambda }^{\mathrm{T}}h(x)$是关于$\lambda$的线性函数，既是凸函数也是凹函数，$-\frac{1}{2\rho }\Vert \lambda -\bar{\lambda }{\Vert }^2$是关于$\lambda$的严格凹函数，因此整个函数仍为严格凹，对于严格凹问题${\max }_{\lambda }f(x)+{\lambda }^{\mathrm{T}}h(x)-\frac{1}{2\rho }\Vert \lambda -\bar{\lambda }{\Vert }^2$有唯一最优解${\lambda }^{\ast }$满足：
$$\frac{\partial \left\{f(x)+{\lambda }^{\top }h(x)-\frac{1}{2\rho }\Vert \lambda -\lambda {\Vert }^2\right\}}{\partial \lambda }=h(x)-\frac{1}{\rho }(\lambda -\bar{\lambda })=0$$
可解得${\lambda }^{\ast }(\bar{\lambda })=\bar{\lambda }+\rho h(x)$，即最优解${\lambda }^{\ast }$是关于$\lambda$的函数。将${\lambda }^{\ast }$带入原问题：
$$\begin{array}{rl}& \underset{x}{\min }\underset{\lambda }{\max }f(x)+{\lambda }^{\mathrm{T}}h(x)-\frac{1}{2\rho }\Vert \lambda -\bar{\lambda }{\Vert }^2\\ =& \underset{x}{\min }f(x)+{\lambda }^{\ast }(\bar{\lambda }{)}^{\mathrm{T}}h(x)-\frac{1}{2\rho }{\Vert {\lambda }^{\ast }(\bar{\lambda })-\bar{\lambda }\Vert }^2\\ =& \underset{x}{\min }f(x)+(\bar{\lambda }+\rho h(x){)}^{\mathrm{T}}h(x)-\frac{\rho }{2}\Vert h(x){\Vert }^2\\ =& \underset{x}{\min }f(x)+{\bar{\lambda }}^{\mathrm{T}}h(x)+\frac{\rho }{2}\Vert h(x){\Vert }^2\end{array}$$

此时得到一个与原问题近似的无约束最优化问题，可以用例如L-BFGS方法求解。这就是PHR-ALM的基本思路，通过在原拉格朗日函数的基础之上增加一个增广项获得一个增广拉格朗日函数$\mathcal{L}(x,\lambda ;\rho )$，来得到近似光滑且容易解的优化问题。为了更接近于原问题，有两种措施：（1）使$\frac{1}{\rho }\to 0$ 或者 $\rho \to +\infty$，以获取二次罚函数的效果，但$\rho$如果很大则和前面分析的罚函数缺陷一样，成为一个Hessian矩阵条件数爆炸的病态问题；（2）迭代更新先验值$\bar{\lambda }\leftarrow {\lambda }^{\ast }(\bar{\lambda })$。

下面介绍一种更为常用的增广拉格朗日函数形式。在迭代过程中，子内循环无约束优化问题$x^{k+1}={\mathrm{argmin}}_x{\mathcal{L}}_{{\rho }^k}\left(x,{\lambda }^k\right)$每次都不需要求解很精确的$x^k$，因为外循环会不断细化${\lambda }^k$和$x^k$。

不等式约束非凸优化问题的PHR-ALM

对于不等式约束的非凸问题，核心思想是通过引入松弛变量$s$，将不等式约束转化为等式约束，然后再写成增广拉格朗日函数形式。如下图所示，引入松弛变量$s$，原问题维度从n维上升到n+m维。原问题为：
$$\begin{array}{rl}{\min }_{x\in {\mathbb{R}}^n}& f(x)\\ \text{ s.t. }& g(x)\le 0\end{array}$$
引入松弛变量后变为等式约束的非凸优化问题：
$$\begin{array}{rl}& \underset{x\in {\mathbb{R}}^n,s\in {\mathbb{R}}^m}{\min }f(x)\\ & \text{ s.t. }g(x)+[s{]}^2=0\\ & \end{array}$$
将转化后的问题写成增广拉格朗日函数形式：
$$\underset{x\in {\mathbb{R}}^n,s\in {\mathbb{R}}^m}{\min }f(x)+\frac{\rho }{2}{\Vert g(x)+[s{]}^2+\frac{\lambda }{\rho }\Vert }^2=\underset{x\in {\mathbb{R}}^n}{\min }\underset{s\in {\mathbb{R}}^m}{\min }f(x)+\frac{\rho }{2}{\Vert g(x)+[s{]}^2+\frac{\lambda }{\rho }\Vert }^2=\underset{x\in {\mathbb{R}}^n}{\min }f(x)+\frac{\rho }{2}{\Vert \max \left[g(x)+\frac{\lambda }{\rho },0\right]\Vert }^2$$
为与等式约束的拉格朗日乘子$\lambda$区分开，将不等式约束非凸问题的增广拉格朗日函数写成：
$${\mathcal{L}}_{\rho }(x,\mu ):=f(x)+\frac{\rho }{2}{\Vert \max \left[g(x)+\frac{\mu }{\rho },0\right]\Vert }^2$$
更新拉格朗日乘子${\mu }^{k+1}={\mu }^k+\rho h(x^{k+1})={\mu }^k+\rho \left(g\left(x^{k+1}\right)+{\left[s^{k+1}\right]}^2\right)$。对于$g\left(x^{k+1}\right)+{\left[s^{k+1}\right]}^2$，当$g\left(x^{k+1}\right)>0$，取$[s{]}^2$=0，当$g\left(x^{k+1}\right)\le 0$，取$[s{]}^2=\left|g\left(x^{x+1}\right)\right|$，因此有$g\left(x^{k+1}\right)+{\left[s^{k+1}\right]}^2=\max \left[g\left(x^{k+1}\right),0\right]$。综上，可消除松弛变量的影响从而得到：
$${\mu }^{k+1}=\max \left[{\mu }^k+\rho g\left(x^{k+1}\right),0\right]$$

求证：${\min }_{x\in {\mathbb{R}}^n}{\min }_{s\in {\mathbb{R}}^m}f(x)+\frac{\rho }{2}{\Vert g(x)+[s{]}^2+\frac{\lambda }{\rho }\Vert }^2={\min }_{x\in {\mathbb{R}}^n}f(x)+\frac{\rho }{2}{\Vert \max \left[g(x)+\frac{\lambda }{\rho },0\right]\Vert }^2$

证明：在前述问题中，已知${\min }_{x\in {\mathbb{R}}^n,s\in {\mathbb{R}}^m}f(x)+\frac{\rho }{2}{\Vert g(x)+[s{]}^2+\frac{\lambda }{\rho }\Vert }^2$ 等价于 ${\min }_{x\in {\mathbb{R}}^n}{\min }_{s\in {\mathbb{R}}^m}f(x)+\frac{\rho }{2}{\Vert g(x)+[s{]}^2+\frac{\lambda }{\rho }\Vert }^2$

对于松弛变量$s\in {\mathbb{R}}^m$而言，其最优化问题为：
$$\underset{s\in {\mathbb{R}}^m}{\min }{\Vert g(x)+[s{]}^2+\frac{\lambda }{p}\Vert }^2$$
令$g(x)+\frac{\lambda }{\rho }=a$，有${\min }_{s\in {\mathbb{R}}^m}{\Vert a+[s{]}^2\Vert }^2$，

当$a>0$时，$\min \left({\Vert a+[s{]}^2\Vert }^2\right)=a$，取$[s{]}^2=0$；

当$a\le 0$时，$\min \left({\Vert a+[s{]}^2\Vert }^2\right)=0$，取$[s{]}^2=|a|$。

所以，
$$\underset{s\in {\mathbb{R}}^m}{\min }{\Vert g(x)+[s{]}^2+\frac{\lambda }{\rho }\Vert }^2={\Vert \max \left[g(x)+\frac{\lambda }{\rho },0\right]\Vert }^2$$

对于一般非凸优化问题的PHR-ALM

结合等式约束和不等式约束的分析，直接将等式约束拉格朗日函数的增广项和不等式约束拉格朗日函数的增广项相加，得到：
$${\mathcal{L}}_{\rho }(x,\lambda ,\mu ):=f(x)+\frac{\rho }{2}\left\{{\Vert h(x)+\frac{\lambda }{\rho }\Vert }^2+{\Vert \max \left[g(x)+\frac{\mu }{\rho },0\right]\Vert }^2\right\}$$

---

参考文献

机器人中的数值优化

最优化：建模、算法与理论/最优化计算方法