深入理解 BPF map 实现机制

article/2025/9/19 22:45:05

揭秘 BPF map 前生今世

目录

  • 揭秘 BPF map 前生今世
    • 1. 前言
    • 2. 简单的使用样例
      • 用户空间与内核 BPF 辅助函数参数对比
    • 3. 深入指令分析
      • 3.1 查看 BPF 指令
      • 3.2 加载器创建 map 对象
      • 3.3 第一次变身： map fd 替换
      • 3.4 第二次变身： map fd 替换成 map 结构指针
    • 4. 整个流程总结
    • 参考

本文地址：https://www.ebpf.top/post/map_internal

1. 前言

众所周知，map 可用于内核 BPF 程序和用户应用程序之间实现双向的数据交换， 为 BPF 技术中的重要基础数据结构。

在 BPF 程序中可以通过声明 struct bpf_map_def 结构完成创建，这其实带给我们一种错觉，感觉这和普通的 C 语言变量没有区别，然而事实真的是这样的吗？ 事情远没有这么简单，读完本文以后相信你会有更大的惊喜。

struct bpf_map_def SEC("maps") my_map = {.type = BPF_MAP_TYPE_ARRAY,// ...
};

我们知道最终 BPF 程序是需要在内核中执行，但是 map 数据结构是用于用户空间和内核 BPF 程序双向的数据结构，那么问题来了：

  • 通过 struct bpf_map_def 定义的变量究竟是如何创建的，是在用户空间创建还是内核中直接创建的？

  • 如何实现创建后的 map 的结构，在用户空间与内核中 BPF 程序关联？你可能注意到在用户空间中对于 map 的访问是通过 map 文件句柄 fd 完成（类型为 int），但是在 BPF 程序中是通过 struct bpf_map * 结构完成的。

毕竟数据交换跨越了用户空间和内核空间，本文将从深入浅出为各位看官揭开 map 整个生命管理的 “大瓜”。

2. 简单的使用样例

本样例来自于 samples/bpf/sockex1_user.c 和 sockex1_kern.c，略有修改和删除。

sockex1_user.c 用户空间程序主要内容如下（为方便展示，部分内容有删除和修改）：

int main(int argc, char **argv)
{struct bpf_object *obj;int map_fd, prog_fd;// ...// 加载 BPF 程序至 bpf_object 对象中，bpf_prog_load("sockex_kern.o", BPF_PROG_TYPE_SOCKET_FILTER, &obj, &prog_fd))// 获取 my_map 对应的 map_fd 句柄map_fd = bpf_object__find_map_fd_by_name(obj, "my_map"); // == 本次关注 ==// 通过 setsockopt 将 BPF 字节码加载到内核中sock = open_raw_sock("lo");setsockopt(sock, SOL_SOCKET, SO_ATTACH_BPF, &prog_fd, sizeof(prog_fd))；popen("ping -4 -c5 localhost", "r"); // 产生报文// 从 my_map 中读取 5 次 IPPROTO_TCP 的统计for (i = 0; i < 5; i++) { long long tcp_cnt;int key = IPPROTO_TCP;assert(bpf_map_lookup_elem(map_fd, &key, &tcp_cnt) == 0); // == 本次关注 ==// ...sleep(1);}return 0;
}

sockex1_user.c 文件中的 bpf_map_lookup_elem 调用的函数原型如下，定义在文件 tools/lib/bpf/bpf.c 中：

int bpf_map_lookup_elem(int fd, const void *key, void *value)

函数底层通过 sys_bpf(cmd=BPF_MAP_LOOKUP_ELEM，...) 实现，为我们方便 map 操作的用户空间封装函数， bpf 系统调用可参考 man 2 bpf。

其中 sockex1_kern.c 主要内容如下：

// map 定义 
struct bpf_map_def SEC("maps") my_map = {.type = BPF_MAP_TYPE_ARRAY,.key_size = sizeof(u32),.value_size = sizeof(long),.max_entries = 256,
};// BPF 程序，获取到报文协议类型并进行计数更新
SEC("socket1")
int bpf_prog1(struct __sk_buff *skb)
{int index = load_byte(skb, ETH_HLEN + offsetof(struct iphdr, protocol));long *value;value = bpf_map_lookup_elem(&my_map, &index);  // 查找索引并更新 map 对应的值，== 本次关注 ==if (value)__sync_fetch_and_add(value, skb->len);return 0;
}
char _license[] SEC("license") = "GPL";

sockex1_kern.c 文件中的 bpf_map_lookup_elem 函数为内核中提供的 BPF 辅助函数，原型声明如下，详情可参考 man 7 bpf-helper：

void *bpf_map_lookup_elem(struct bpf_map *map, const void *key)

用户空间与内核 BPF 辅助函数参数对比

通过分析 sockex1_user.c 和 sockex1_kern.c 函数中的 bpf_map_lookup_elem 使用姿势，这里我们做个简单对比：

// 用户空间 map 查询函数
int bpf_map_lookup_elem(int fd, const void *key, void *value)// 内核中 BPF 辅助函数 map 查询函数
void *bpf_map_lookup_elem(struct bpf_map *map, const void *key)

那么如何将 int fd 与 struct bpf_map *map 共同关联一个对象呢？ 这需要我们通过分析 BPF 字节码来进行解密。

3. 深入指令分析

首先我们将 sockex1_kern.c 文件使用 llvm/clang 将之编译成 ELF 的 BPF 字节码。对于生成的 sockex1_kern.o 文件可以用 llvm-objdump 来查看相对应的文件格式，这里我们仅关注 map 相关的部分。

3.1 查看 BPF 指令

$ clang -O2 -target bpf -c sockex1_kern.c  -o sockex1_kern.o
$ llvm-objdump -S sockex1_kern.o0000000000000000 <bpf_prog1>:// ...; 	value = bpf_map_lookup_elem(&my_map, &index); # 备注：编译的机器启用了 BTF 7:	18 01 00 00 00 00 00 00 00 00 00 00 00 00 00 00	r1 = 0 ll9:	85 00 00 00 01 00 00 00	call 1// ...

上述结果展示了 BPF 程序中 socket1 部分的函数 bpf_prog1 的 BPF 指令，但是其中对于涉及到的变量 my_map 的引用都未有解决。上述的反汇编部分打印了 map_lookup_elem() 函数调用涉及的指令：

  • 根据 BPF 程序调用的约定，寄存器 r1 为函数调用的第 1 个参数，这里即 bpf_map_lookup_elem(&my_map, &index) 调用中的 my_map 。
       7:	18 01 00 00 00 00 00 00 00 00 00 00 00 00 00 00	r1 = 0 ll  # 64 位直接数赋值 , r1 = 0 9:	85 00 00 00 01 00 00 00	call 1                             # 调用 bpf_map_lookup_elem，编号为 1

上述 “7:” 行 表了为一条 16 个字节的 BPF 指令，表示加载一个 64 位立即数。

这里无需担心相关的 BPF 指令集，后续我们会详细展开解释。1 个 BPF 指令有 8 个字节组成，格式定义如下：

struct bpf_insn {__u8    code;         /* opcode */__u8    dst_reg:4;    /* dest register */__u8    src_reg:4;    /* source register */__s16   off;        /* signed offset */__s32   imm;        /* signed immediate constant */
};

通过上述结构对应拆解一下 ”7:“ 行（其中包含了 2 条 BPF 指令，为 BPF 指令中的特殊指令，运行时会被解析成 1 条指令执行） ，第 1 条 BPF 指令详细的信息如下：（这里忽略了 off 字段）

  • opcode 为 0x18，即 BPF_LD | BPF_IMM | BPF_DW。该 opcode 表示要将一个 64 位的立即数加载到目标寄存器。
  • dst_reg 是 1（4 个 bit 位），代表寄存器 r1。
  • src_reg 是 0（4 个 bit 位），表示立即数在指令内。
  • imm 为 0，因为 my_map 的值在生成 BPF 字节码的时候还未进行创建。

第 2 条指令主要负责保存 imm 的高 32 位。

3.2 加载器创建 map 对象

当加载器（loader）在加载 ELF 对象 sockex1_kern.o 时，其首先会从 ELF 格式的 maps 区域获取到定义的 map 对象 my_map 及相关的属性， 然后通过调用 bpf() 系统调用来创建 my_map 对象，如果创建成功，那么 bpf() 系统调用返回一个文件描述符 (map fd)。

同时，加载器也会对于基于 map 元信息（比如名称 my_map）与通过 bpf() 系统调用创建 map 后返回的 map fd 建立起对应关系，此后用户空间空间程序就可以使用 my_map 作为关键字获取到其对应的 fd，具体代码如下：

map_fd = bpf_object__find_map_fd_by_name(obj, "my_map");

用户空间获取到了 map 对象的 fd，后续可用于 map_lookup_elem（map_fd, ...) 函数进行 map 的查询等操作。

3.3 第一次变身： map fd 替换

以上完成了 my_map 对象的创建，但是在 BPF 字节码程序加载到内核前，还需要将 map fd 在 BPF 指令集中完成第一次变身，如函数 lib/bpf.c: bpf_apply_relo_map() 的代码片段所示：

        prog->insns[insn_off].src_reg = BPF_PSEUDO_MAP_FD; // 值在内核中定义为 1prog->insns[insn_off].imm = ctx->map_fds[map_idx]; // ctx->map_fds[map_idx] 即为保存的 map fd 值。

这里假设获取到的 map 文件描述符为 6，那么在加载的 BPF 程序完成 bpf_apply_relo_map 的替换后上述的指令对比如下：

ELF 文件中的字节码：

       7:	18 01 00 00 00 00 00 00 00 00 00 00 00 00 00 00	r1 = 0 ll  # 64 位直接数赋值 , r1 = 0 9:	85 00 00 00 01 00 00 00	call 1                             # 调用 bpf_map_lookup_elem，编号为 1

替换 map fd 后的字节码：

       7:	18 11 00 00 06 00 00 00 00 00 00 00 00 00 00 00	r1 = 0 ll  # 64 位直接数赋值 , r1 = 6 9:	85 00 00 00 01 00 00 00	call 1                             # 调用 bpf_map_lookup_elem，编号为 1

3.4 第二次变身： map fd 替换成 map 结构指针

当上述经过第一次变身的 BPF 字节码加载到内核后，还需要进行一次变身，才能真正在内核中工作，这次 BPF 验证器（verifier）扛过大旗。

验证器将加载器注入到指令中的 map fd 替换成内核中的 map 对象指针。调用堆栈的情况如下：

    sys_bpf()--> bpf_prog_load()--> bpf_check()--> replace_map_fd_with_map_ptr()--> do_check()--> check_ld_imm()==> check_func_arg()--> convert_pseudo_ld_imm64()

函数 replace_map_fd_with_map_ptr() 通过以下代码完成第二次大变身，实现了内核中 BPF 字节码的 imm 摇身一变成为 map ptr 地址。

        f = fdget(insn[0].imm);  // 从第 1 条指令中的 imm 字段获取到加载器设置的 map fdmap = __bpf_map_get(f);  // 基于 map fd 获取到 map 对象指针addr = (unsigned long)map;  insn[0].imm = (u32)addr;   // 将 map  对象指针低 32 位放入第一条指令中的 imm 字段insn[1].imm = addr >> 32;  // 将 map  对象指针高 32 位放入第二条指令中的 imm 字段

于此同时，函数 convert_pseudo_ld_imm64() 还需要清理加载器设置的 src_reg = BPF_PSEUDO_MAP_FD 操作（ prog->insns[insn_off].src_reg = BPF_PSEUDO_MAP_FD;）， 用于表明完成了整个指令的重写工作：

        if (insn->code == (BPF_LD | BPF_IMM | BPF_DW))insn->src_reg = 0;

如果这里的 my_map 在内核中 64 位地址为 0xffff8881384aa200，那么验证器完成第二次变身后的 BPF 字节码对比如下。

替换 map fd 后的字节码：

       7:	18 11 00 00 06 00 00 00 00 00 00 00 00 00 00 00	r1 = 0 ll  # 64 位直接数赋值 , r1 = 6 9:	85 00 00 00 01 00 00 00	call 1                             # 调用 bpf_map_lookup_elem，编号为 1

替换为 map 对象指针后的字节码如下：

      7： 18 01 00 00 00 a2 4a 38 00 00 00 00 81 88 ff ff           # 64 位直接数赋值 , r1 = 0xffff8881384aa200 9： 85 00 00 00 30 86 01 00																	 # 调用 bpf_map_lookup_elem，编号为 1

在完成了上述两次变身后，当在内核中调用 map_lookup_elem() 时，第一个参数 my_map 的值为 0xffff8881384aa200，

从而实现了从最早的 ELF 中的 0 ，替换成了 map_fd (6)，直到最后的 map 对象 struct bpf_map * (0xffff8881384aa200)。

提示，内核中 bpf_map_lookup_elem 辅助函数的原型定义为：

static void *(*bpf_map_lookup_elem)(struct bpf_map *map, void *key)

4. 整个流程总结

通过上述 map 访问指令的 2 次大变身，我们可以清晰了解 map 创建、map fd 指令重写和 map ptr 对象的重写，也能够彻底明白用户空间 map fd 与内核中 map 对象指针的关联关系。

俗话说一图胜千言，这里我们用一张图进行整个流程的总结：

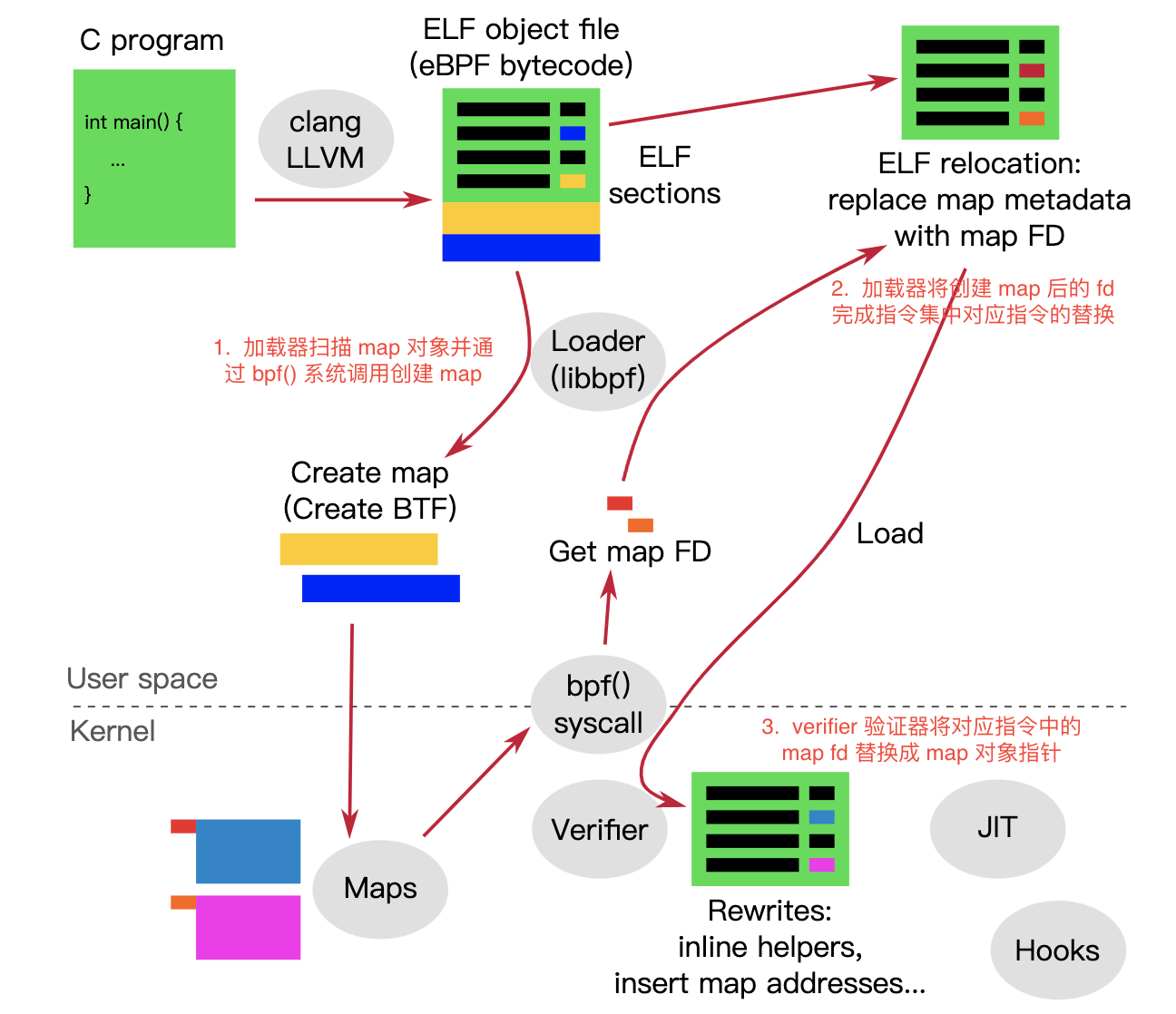
原始图片来自于这里 ，略有修改。

参考

  • Linux bpf map internals
  • eCHO episode 11: Exploring bpftool with Quentin Monnet
  • ebpf: BPF_FUNC_map_lookup_elem calling convention
  • 边缘网络 eBPF 超能力：eBPF map 原理与性能解析

http://chatgpt.dhexx.cn/article/DAsdlhhL.shtml

相关文章

bpf简介1

bpf简介1

文章目录 前言prefaceIntroduction历史发展结构 推荐阅读 前言 来源&#xff1a;Linux Observability with BPF 这里整理下该书第一章&#xff1a;preface && Introduction 这本书有中文版的《Linux内核观测技术BPF》。这个链接里面的资料也是很好的&#xff0c;可以…
阅读更多...
BPF技术学习分享

BPF技术学习分享

什么是BPF程序&#xff1a; BPF is a highly flexible and efficient virtual machine-like construct in the Linux kernel allowing to execute bytecode at various hook points in a safe manner. BPF程序 ----LLVMClang----> BPF字节码 ----JIT----> BPF指令集&…
阅读更多...
BPF之事件源

BPF之事件源

基础 1. BPF和eBPF概念 BPF 原是 Berkeley Packet Filter&#xff08;伯克利数据包过滤器&#xff09;的缩写&#xff0c;1992诞生&#xff0c;用于网络包过滤。2014经过修改并入 Linux 内核主线&#xff0c;从此 BPF 变成了一个更通用的执行引擎&#xff0c;主要用于网络、可…
阅读更多...
DPDK BPF

DPDK BPF

DPDK BPF DPDK 自版本 18.05 已集成了 librte_bpf, 主要利用rte_eth_rx_burst/rte_eth_tx_burst 回调函数机制, 执行eBPF字节码. 当前支持以下特性: base eBPF ISA (except tail-pointer)JIT (x86_64 and arm64 only)eBPF code verifieruser-defined helper functions (64-bi…
阅读更多...
Linux超能力BPF技术介绍及学习分享

Linux超能力BPF技术介绍及学习分享

近两年BPF技术跃然成为了一项热门技术&#xff0c;在刚刚结束的KubeCon 2020 Europe会议上有7个关于BPF的技术分享&#xff0c; 而在KubeCon 2020 China会议上也已有了3个关于BPF技术的中文分享&#xff0c;分别来自腾讯和PingCAP&#xff0c;涉足网络优化和系统追踪等领域。在…
阅读更多...
bpf原理与入门

bpf原理与入门

一、bpf架构 如上图所示，bpf由六部分构成，以下为其在bpf中的作用： bpf工具：该部分涉及bpf用户态程序、bpf的编译工具，通过bpf编译工具如Clang、LLVM将bpf用户态程序编译成bpf字节码； 加载器：可以简单理解为bpf系统调用，将bpf字节码加载到内核； 验证器：对bpf程序的…
阅读更多...
BPF入门1：BPF技术简介

BPF入门1：BPF技术简介

目录 cbpf 介绍ebpf 介绍ebpf 和 cbpf对比ebpf和内核模块的对比 ebpf应用ebpf架构Why BPF is FAST指令虚拟机JIT How BPF extends KernelLLVM 编写ebpf程序BCCBPFTraceC 语言原生方式 国内大厂使用ebpf的实践经验参考 cbpf 介绍 BPF&#xff08;Berkeley Packet Filter &#…
阅读更多...
增广拉格朗日函数

增广拉格朗日函数

对于优化问题 arg ⁡ min ⁡ z E ( z ) ( 1 a ) s . t . C z − b 0 ( 1 b ) \mathop{\arg\min}_{z} \ E(z)\qquad(1a)\\ s.t. \quad Cz-b0 \qquad(1b) argminz​ E(z)(1a)s.t.Cz−b0(1b) 其增广拉格朗日函数被定义为&#xff1a; L ( z , α , μ ) E ( z ) α T ( C z −…
阅读更多...
约束优化：PHR-ALM 增广拉格朗日函数法

约束优化：PHR-ALM 增广拉格朗日函数法

文章目录 约束优化&#xff1a;PHR-ALM 增广拉格朗日函数法等式约束非凸优化问题的PHR-ALM不等式约束非凸优化问题的PHR-ALM对于一般非凸优化问题的PHR-ALM参考文献 约束优化&#xff1a;PHR-ALM 增广拉格朗日函数法 基础预备&#xff1a; 约束优化&#xff1a;约束优化的三种…
阅读更多...
matlab编写拉格朗日插值代码函数

matlab编写拉格朗日插值代码函数

要求&#xff1a;根据拉格朗日多项式插值法原理&#xff0c;设计算法流程并且编写拉格朗日插值代码函数。 代码如下&#xff1a; function[y]lagrange(x0,y0,x) %建立一个函数名为lagrange的函数&#xff0c;输入x0,y0为插值点的坐标&#xff0c;均为数组&#xff0c;x为要…
阅读更多...
拉格朗日函数最优化问题

拉格朗日函数最优化问题

目的&#xff1a;将有约束条件的函数最优化问题通过拉格朗日函数转化为无条件的函数最优化问题。 条件极值最优化问题&#xff1a; 对于无条件的函数最优化问题&#xff0c;常用的有3种方式&#xff1a; 梯度下降&#xff1a;求解一阶导数&#xff0c;其实就是使用泰勒一阶展…
阅读更多...
【深度学习】拉格朗日（ Lagrange）中值定理

【深度学习】拉格朗日（ Lagrange）中值定理

文章目录 1、定理2、几何意义3、证明思路4、有限增量定理5、推论1、定理 如果函数 f(x) 满足： 在闭区间[a,b]上连续； 在开区间(a,b)内可导。 那么在(a,b)内至少有一点ξ(a<ξ<b)，使等式 ： f(b)-f(a)=f′(ξ)(b-a) 成立，或： f′(ξ) =(f(b)-f(a)) / (b-a) 或存…
阅读更多...
拉格朗日（lagrange)插值及其MATLAB程序

拉格朗日（lagrange)插值及其MATLAB程序

一、n次拉格朗日插值 根据《插值多项式的性质》中的定理6.1可得 其中&#xff08;6.19&#xff09;称为基函数&#xff0c;&#xff08;6.18&#xff09;称为拉格朗日多项式&#xff0c;用&#xff08;6.18&#xff09;计算插值称为拉格朗日多项式插值。 方法2&#xff1a;通过…
阅读更多...
拉格朗日函数优化

拉格朗日函数优化

等式约束最优化 可以写为&#xff1a; 引入拉格朗日乘子&#xff08;&#xff09;把问题转换成拉格朗日函数 因为对于任何可行解&#xff0c;有&#xff0c;所以有 &#xff0c;也就是&#xff0c;。 求解。对分别求的偏导数为零&#xff0c;得到方程组求解极值点&#xff0c…
阅读更多...
增广拉格朗日函数法

增广拉格朗日函数法

增广拉格朗日函数法 在二次罚函数法中&#xff0c;为了保证可行性&#xff0c;罚因子必须趋于正无穷。此时&#xff0c;子问题因条件数爆炸而难以求解。那么&#xff0c;是否可以通过对二次罚函数进行某种修正&#xff0c;使得对有限的罚因子&#xff0c;得到的毕竟最优解也是…
阅读更多...
增广拉格朗日函数法（ALM）

增广拉格朗日函数法（ALM）

增广拉格朗日函数法&#xff08; Augmented Lagrangian method&#xff09; 一、等式约束 考虑问题&#xff1a; min ⁡ x f ( x ) s . t . c i ( x ) 0 , i 1 , ⋯ , m . \begin{array}{ll} \min_x &f(x)\\ s.t. &c_i(x) 0, \quad i1,\cdots,m. \end{array} min…
阅读更多...
广义拉格朗日函数的理解

广义拉格朗日函数的理解

1、拉格朗日函数&#xff1a; 求极值 求函数f(x,y,z)在条件φ(x,y,z)0下的极值 方法&#xff08;步骤&#xff09;是&#xff1a; 1.做拉格朗日函数Lf(x,y,z)λφ(x,y,z),λ称拉格朗日乘数 2.求L分别对x,y,z,λ求偏导,得方程组,求出驻点P(x,y,z) 如果这个实际问题的最大或…
阅读更多...
各种拉格朗日函数

各种拉格朗日函数

目录 一&#xff0c;拉格朗日函数 二&#xff0c;部分拉格朗日函数 三&#xff0c;增广拉格朗日函数 一&#xff0c;拉格朗日函数 以三元函数为例&#xff1a; 求f(x,y,z)的极值&#xff0c;s.t.g(x,y,z)0 拉格朗日函数L(x,y,z,a) f(x,y,z) a * g(x,y,z) 在极值点处一…
阅读更多...
拉格朗日函数相关推导

拉格朗日函数相关推导

优化问题&#xff08;即高数中的求极值&#xff09;可分为三类&#xff1a;无约束、等式约束、不等式约束。 对于无约束的优化问题&#xff1a;求导&#xff0c;令导数为零即可求解。 等式约束优化&#xff1a;&#xff08;拉格朗日乘子法最开始就是求解等式约束优化的方法&…
阅读更多...
HJ-浇花

HJ-浇花

链接&#xff1a;https://ac.nowcoder.com/acm/contest/322/M 来源&#xff1a;牛客网 时间限制&#xff1a;C/C 1秒&#xff0c;其他语言2秒 空间限制&#xff1a;C/C 32768K&#xff0c;其他语言65536K 64bit IO Format: %lld 题目描述 HJ养了很多花&#xff08;9999999…
阅读更多...
推荐文章

Copyright @ 2022~2023