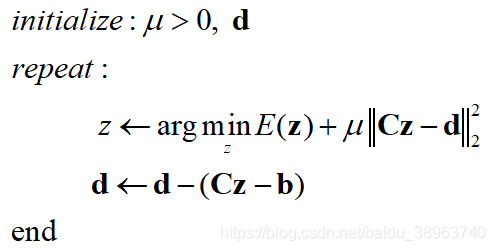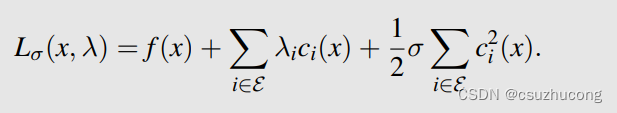对于优化问题
arg min z E ( z ) ( 1 a ) s . t . C z − b = 0 ( 1 b ) \mathop{\arg\min}_{z} \ E(z)\qquad(1a)\\ s.t. \quad Cz-b=0 \qquad(1b) argminz E(z)(1a)s.t.Cz−b=0(1b)
其增广拉格朗日函数被定义为:
L ( z , α , μ ) = E ( z ) + α T ( C z − b ) + μ ∣ ∣ C z − b ∣ ∣ 2 2 L(z,\alpha,\mu)=E(z)+\alpha^T(Cz-b)+\mu||Cz-b||_{2}^2 L(z,α,μ)=E(z)+αT(Cz−b)+μ∣∣Cz−b∣∣22
其中, α \alpha α为拉格朗日乘数。 μ \mu μ为步长参数,它的取值会影响算法的收敛速度。但它并不影响它收敛的解。
约束问题的解法如下: