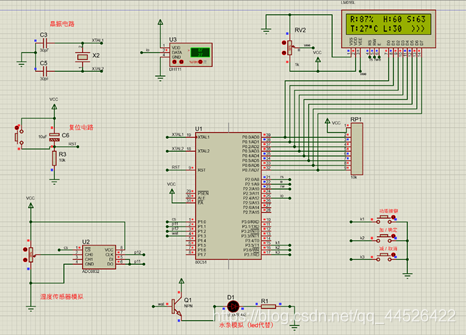
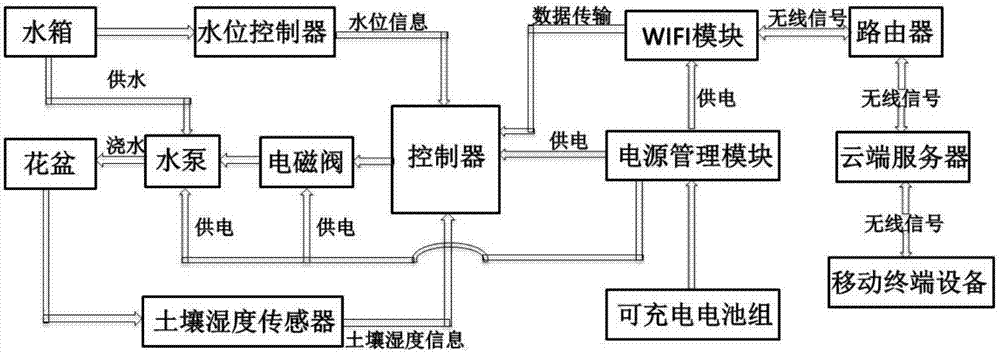
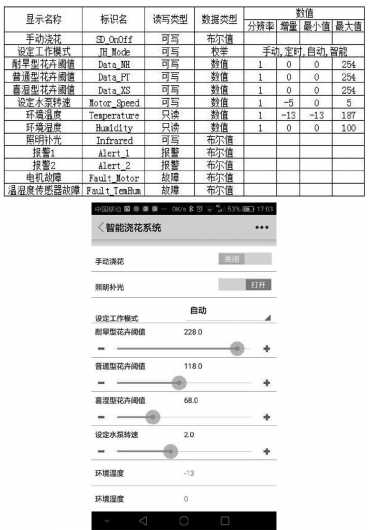
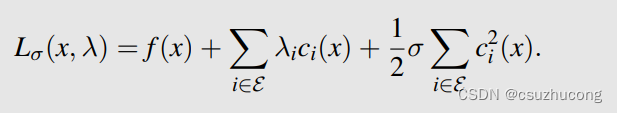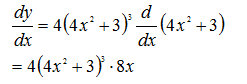增广拉格朗日函数法

在二次罚函数法中，为了保证可行性，罚因子必须趋于正无穷。此时，子问题因条件数爆炸而难以求解。那么，是否可以通过对二次罚函数进行某种修正，使得对有限的罚因子，得到的毕竟最优解也是可行的？增广拉格朗日函数法就是这样的一个方法。

一、等式约束优化问题的增广拉格朗日函数法

1. 增广拉格朗日函数法的构造
   增广拉格朗日函数法的每一步构造一个增广拉格朗日函数，而该函数的构造依赖于拉格朗日函数和约束的二次罚函数。具体地，对于等式约束优化问题，
   $$\begin{array}{rl}& \underset{x}{\min }f(x)\\ & s.t.c_i(x)=0,i\in \mathcal{E}\end{array}\text{\hspace{1em}(1)}$$
   其增广拉格朗日函数定义为
   $$L_{\sigma }(x,\lambda )=f(x)+\sum _{i\in \mathcal{E}}{\lambda }_i{c}_i(x)+\frac{1}{2}\sum _{i\in \mathcal{E}}{c}_i^2(x),\text{\hspace{1em}(2)}$$
   即在拉格朗日函数的基础上，添加约束的二次罚函数。在第k步迭代，给定罚因子${\sigma }_k$和橙子${\lambda }^k$，增广拉格朗日函数$L_{{\sigma }_k}(x,{\lambda }^k)$的最小值点$x^{k+1}$满足
   $${\nabla }_x{L}_{{\sigma }_k}(x^{k_1},{\lambda }^k)=\nabla f(x^{k+1})+\sum _{i\in \mathcal{E}}({\lambda }_i^k+{\sigma }_k{c}_i(x^{k+1}))\nabla c_i(x^{k+1})=0\text{\hspace{1em}(3)}$$
   对于优化问题（1），其最优解$x^{\ast }$以及相应的乘子${\lambda }^{\ast }$需要满足
   $$\nabla f(x^{\ast })+\sum _{i\in \mathcal{E}}{\lambda }_i^{\ast }\nabla c_i(x^{\ast })=0\text{\hspace{1em}(4)}$$
   为使增广拉格朗日函数法产生的迭代点列收敛到$x^{\ast }$，需要保证等式（3）（4）在最优解处的一致性。因此，对于充分大的$k$，
   $${\lambda }_i^{\ast }\approx {\lambda }_i^k+{\sigma }_k{c}_i(x^{k+1}),\forall i\in \mathcal{E}$$
   上式等价于
   $$c_i(x^{k+1})\approx \frac{1}{{\sigma }_k}({\lambda }_i^{\ast }-{\lambda }_i^k)\text{\hspace{1em}(5)}$$
   所以，当${\lambda }_i^k$足够接近${\lambda }_i^{\ast }$时，点$x^{k+1}$处的约束违反度将会远小于$\frac{1}{{\sigma }_k}$。注意，在（1）式中约束违反度式正比于$\frac{1}{{\sigma }_k}$的。即增广拉格朗日函数法可以通过有效地更新乘子来降低约束违反度，（5）式表明，橙子的一个有效的更新格式为
   $${\lambda }_i^{k+1}={\lambda }_i^k+{\sigma }_k{c}_i(x^{k+1}),\forall i\in \mathcal{E}$$
   那么，我们得到问题（1）的增广拉格朗日函数法，见算法1，其中$c(x)=[c_i(x){]}_{i\in \mathcal{E}}$，并且$\nabla c(x)=[\nabla c_i(x){]}_{i\in \mathcal{E}}$

---

算法1：增广拉格朗日函数法

1. 选取初始点$x^0$，乘子${\lambda }^0$，罚因子更新常数$\rho >0$，约束违反度常数$ϵ>0$和精度要求${\eta }_k>0$。并令$k=0$.
2. for k=0,1,2,$\cdots$do
3. \quad 以$x^k$为初始点，求解${\min }_x{L}_{{\sigma }_k}(x,{\lambda }_k)$，得到满足精度条件$||{\nabla }_x{L}_{{\sigma }_k}(x,{\lambda }^k)||\le {\eta }_k$的解$x^{k+1}$
4. \quad if $||c(x^{k+1})||\le ϵ$ then
5. \qquad 返回近似解$x^{k+1},{\lambda }^k$，终止迭代
6. \quad end if
7. \quad 更新乘子：${\lambda }^{k+1}={\lambda }^k+{\sigma }_{k}c(x^{k+1})$
8. \quad 更新罚因子：${\sigma }_{k+1}=\rho {\sigma }_k$
9. end for

---

二、一般约束优化问题的增广拉格朗日函数法
对于一般约束优化问题
$$\begin{array}{rl}\min & f(x)\\ s.t& c_i(x)=0,i\in \mathcal{E}\\ & c_i(x)\le 0,i\in \mathcal{I}\end{array}\text{\hspace{1em}(6)}$$
也可以定义其增广拉个蓝i函数以及涉及相应的增广拉格朗日函数法。在拉格朗日函数的定义中，往往倾向于将简单的约束保留，对复杂的约束引入乘子。这里，对于带不等式约束的优化问题，我们先通过引入松弛变量将不等式约束转化为等式约束和简单的非负约束，再对保留非负约束形式的拉格朗日函数添加等式约束的二次罚函数来构造拉格朗日函数。

1. 增广拉格朗日函数
   对于问题（6），引入松弛变量可以得到如下等价形式
   $$\begin{array}{rl}\underset{x,s}{\min }& f(x),\\ s.t& c_i(x)=0,i\in \mathcal{E},\\ & c_i(x)+s_i=0,i\in \mathcal{I},\\ & s_i\ge 0,i\in \mathcal{I}\end{array}\text{\hspace{1em}(7)}$$
   保留非负约束，可以构造拉格朗日函数
   $$L(x,s,\lambda ,\mu )=f(x)+\sum _{i\in \mathcal{E}}{\lambda }_i{c}_i(x)+\sum _{i\in \mathcal{I}}{\mu }_i(c_i(x)+s_i),s_i\ge 0,i\in \mathcal{I}$$
   记问题（7）中等式约束的二次罚函数为$p(x,s)$，则
   $$p(x,s)=\sum _{i\in \mathcal{E}}{c}_i^2(x)+\sum _{i\in \mathcal{I}}(c_i(x)+s_i{)}^2.$$
   我们构造拉格朗日函数如下：
   $$L(x,s,\lambda ,\mu )=f(x)+\sum _{i\in \mathcal{E}}{\lambda }_i{c}_i(x)+\sum _{i\in \mathcal{I}}{\mu }_i(c_i(x)+s_i)+\frac{\sigma }{2}p(x,s),s_i\ge 0,i\in \mathcal{I}$$
   其中$\sigma$为罚因子

2. 增广拉格朗日函数法
   在第$k$步迭代中，给定乘子${\lambda }_k,{\mu }_k$和罚因子${\sigma }_k$，我们需要求解如下问题:
   $$\underset{x,s}{\min }{L}_{{\sigma }_k}(x,s,{\lambda }_k,{\mu }_k),s.ts\ge 0\text{\hspace{1em}(8)}$$
   以得到$x^{k+1},s^{k+1}$。求解问题（8）的一个有效的方法是投影梯度法。另外一种方法是消去$s$，求解只关于$x$的优化问题。具体地，固定$x$，关于$s$的子问题可以表示为
   $$\underset{s\ge 0}{\min }\sum _{i\in \mathcal{I}}{\mu }_i(c_i(x)+s_i)+\frac{{\sigma }_k}{2}\sum _{i\in \mathcal{I}}(c_i(x)+s_i{)}^2$$
   根据凸优化问题的最优性理论，$s$为以上为题的一个全局最优解，当且仅当
   s i = max ⁡ { − μ i σ k − c i ( x ) , 0 } , i ∈ I (9) s_i=\max\{-\frac{\mu_i}{\sigma_k}-c_i(x),0\},\quad i\in\mathcal{I}\tag{9} si​=max{−σk​μi​​−ci​(x),0},i∈I(9)
   将$s_i$的表达式代入$L_{{\sigma }_k}$我们有
   L σ k ( x , λ k , s i m g a k ) = f ( x ) + ∑ i ∈ I λ i c i ( x ) + σ k 2 ∑ i ∈ E c i 2 + σ k 2 ∑ i ∈ I ( max ⁡ { μ i σ k + c i ( x ) , 0 } 2 − m u i 2 σ k 2 ) (10) L_{\sigma_k}(x,\lambda_k,simga_k)=f(x)+\sum_{i\in\mathcal{I}}\lambda_ic_i(x)+\frac{\sigma_k}{2}\sum_{i\in\mathcal{E}}c_i^2+\frac{\sigma_k}{2}\sum_{i\in\mathcal{I}}(\max\{\frac{\mu_i}{\sigma_k}+c_i(x), 0\}^2-\frac{mu_i^2}{\sigma_k^2}) \tag{10} Lσk​​(x,λk​,simgak​)=f(x)+i∈I∑​λi​ci​(x)+2σk​​i∈E∑​ci2​+2σk​​i∈I∑​(max{σk​μi​​+ci​(x),0}2−σk2​mui2​​)(10)
   其为关于$x$的连续可微函数。因此问题（8）等价于
   $$\underset{x\in {\mathcal{R}}^n}{\min }{L}_{{\sigma }_k}(x,{\lambda }_k,{\mu }_k),$$
   并可以利用梯度法求解。这样做的一个好处是，我们小区了变量$s$，从而在低维空间$R^n$中求解极小点。
   对于问题（7），其最优解$x^{\ast },s^{\ast }$和乘子${\lambda }^{\ast },{\mu }^{\ast }$满足KKT条件：
   $$\begin{array}{rl}0& =\nabla f(x^{\ast })+\sum _{i\in \mathcal{E}}{\lambda }_i^{\ast }\nabla c_i(x^{\ast })+\sum _{i\in \mathcal{I}}m{u}_i^{\ast }\nabla c_i(x^{\ast }),\\ {\mu }_i^{\ast }& \ge 0,i\in \mathcal{I},\\ s_i^{\ast }& \ge 0,i\in \mathcal{I}.\end{array}$$
   问题（8）的最优解$x^{k+1},s^{k+1}$满足
   0 = ∇ f ( x k + 1 ) + ∑ i ∈ E ( λ i k + σ k c i ( x k + 1 ) ) ∇ c i ( x k + 1 ) + ∑ i ∈ i ( μ i k + σ k ( c i ( x k + 1 ) + s i k + 1 ) ) ∇ c i ( x k + 1 ) , s i k + 1 = m a x { − m u i k σ k − c i ( x k + 1 ) , 0 } , i ∈ I . \begin{aligned} 0&=\nabla f(x^{k+1})+\sum_{i\in\mathcal{E}}(\lambda_i^k+\sigma_kc_i(x^{k+1}))\nabla c_i(x^{k+1})+\sum_{i\in\mathcal{i}}(\mu_i^k+\sigma_k(c_i(x^{k+1})+s_i^{k+1}))\nabla c_i(x^{k+1}),\\ s_i^{k+1}&=max\{-\frac{mu_i^k}{\sigma_k}-c_i(x^{k+1}), 0\},i\in\mathcal{I}. \end{aligned} 0sik+1​​=∇f(xk+1)+i∈E∑​(λik​+σk​ci​(xk+1))∇ci​(xk+1)+i∈i∑​(μik​+σk​(ci​(xk+1)+sik+1​))∇ci​(xk+1),=max{−σk​muik​​−ci​(xk+1),0},i∈I.​
   对比问题（7）和问题（8）的KKT条件，易知乘子的更新格式为
   λ i k + 1 = λ i k + σ k c i ( x k + 1 ) , i ∈ E μ i k + 1 = m a x { m u i k + σ k c i ( x k + 1 ) , 0 } , i ∈ I \begin{aligned} \lambda_i^{k+1}&=\lambda_i^k+\sigma_kc_i(x^{k+1}),i\in\mathcal{E}\\ \mu_i^{k+1}&=max\{mu_i^k+\sigma_kc_i(x^{k+1}), 0\},i\in\mathcal{I} \end{aligned} λik+1​μik+1​​=λik​+σk​ci​(xk+1),i∈E=max{muik​+σk​ci​(xk+1),0},i∈I​
   对于等式约束，约束违反度定义为
   $$v_k(x^{k+1})=\sqrt{\sum _{i\in \mathcal{E}}{c}_i^2(x^{k+1})+\sum _{i\in \mathcal{I}}(c_i(x^{k+1})+s_i^{k+1}{)}^2}$$
   根据（9）式消去$s$，约束违反度为
   v k ( x k + 1 ) = ∑ i ∈ E c i 2 ( x k + 1 ) + ∑ i ∈ I m a x { c i ( x k + 1 ) , − μ i k σ k } v_k(x^{k+1})=\sqrt{\sum_{i\in\mathcal{E}}c_i^2(x^{k+1})+\sum_{i\in\mathcal{I}}max\{c_i(x^{k+1}),-\frac{\mu_i^k}{\sigma_k}\}} vk​(xk+1)=i∈E∑​ci2​(xk+1)+i∈I∑​max{ci​(xk+1),−σk​μik​​} ​
   综上，我们给出优化问题（8）的增广拉格朗日函数法，见算法2，该算法与算法1结构相似，但它给出了算法参数的一种具体更新方式。每次计算出子问题的近似解$x^{k+1}$后，算法需要判断约束违反度$v_k^{k+1}$是否满足精度。若满足，则进行乘子更新，并提高子问题求解精度，此时罚因子不变；若不满足，则不进行乘子的更新，并适当增大罚因子以便得到约束违反度更小的解。

---

算法2：一般约束优化问题的增广拉格朗日函数法

1. 选取初始点$x^0$，乘子${\lambda }^0,{\mu }^0$，罚因子${\sigma }_0>0$，约束违反度常数$ϵ>0$，精度常数$\eta >0$，以及常数$0<\alpha \le \beta \le 1$和$\rho >1$。令${\eta }_0=\frac{1}{{\sigma }_0},{ϵ}_0=\frac{1}{{\sigma }_0^{\alpha }}$以及$k=0$.
2. for k=0,1,2,$\cdots$do
3. \quad 以$x^k$为初始点，求解${\min }_x{L}_{{\sigma }_k}(x,{\lambda }_k,m{u}_k)$得到满足精度条件$||{\min }_x{L}_{{\sigma }_k}(x,{\lambda }_k,m{u}_k)|{|}_2\le {\eta }_k$的解$x^{k+1}$
4. \quad if $v_k(x^{k+1})\le {ϵ}_k$ then
5. \qquad if $v_k(x^{k+1})\le ϵ$且$||{\min }_x{L}_{{\sigma }_k}(x,{\lambda }_k,m{u}_k)|{|}_2\le \eta$ then
6. \qquad \quad 得到逼近解$x^{k+1},{\lambda }^k,{\mu }^k$，终止迭代。
7. \qquad end if
8. \qquad 更新乘子：
   λ i k + 1 = λ i k + σ k c i ( x k + 1 ) , i ∈ E , μ i k + 1 = m a x { m u i k + σ k c i ( x k + 1 ) , 0 } , i ∈ I \begin{aligned} \lambda_i^{k+1} &= \lambda_i^k+\sigma_kc_i(x^{k+1}),i\in\mathcal{E},\\ \mu_i^{k+1} &= max\{mu_i^k+\sigma_kc_i(x^{k+1}), 0\}, i\in\mathcal{I} \end{aligned} λik+1​μik+1​​=λik​+σk​ci​(xk+1),i∈E,=max{muik​+σk​ci​(xk+1),0},i∈I​
9. \qquad 罚因子不变：${\sigma }_{k+1}={\sigma }_k$
10. \qquad 减小子问题求解误差和约束违反度：${\eta }_{k+1}=\frac{{\eta }_k}{{\sigma }_{k+1}},{ϵ}_{k+1}=\frac{{ϵ}_k}{{\sigma }_{k+1}^{\beta }}$
11. \quad else
12. \qquad 乘子不变：${\lambda }_{k+1}={\lambda }_k$.
13. \qquad 更新罚因子：${\sigma }_{k+1}=\rho {\sigma }_k$.
14. \qquad 调整子问题求解误差和约束违反度：${\eta }_{k+1}=\frac{1}{{\sigma }_{k+1}},{ϵ}_{k+1}=\frac{1}{{\sigma }_{k+1}^{\beta }}$
15. \quad end if
16. end for

---

三、凸优化问题的增广拉格朗日函数法
考虑凸优化问题：
$$\begin{array}{rl}\underset{x\in R^n}{\min }& f(x),\\ s.t& c_i(x)\le 0,i=1,2,\cdots ,m,\end{array}\text{\hspace{1em}(11)}$$
其中$f:R^n\to R,c_i:R^n\to R,i=1,2,\cdots ,m$为闭凸函数。为了叙述的方便，这里考虑不等式形式的凸优化问题。定义可行域为 χ = { x ∣ c i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , m } \chi=\{x|c_i(x)\le 0, i=1,2,\cdots,m\} χ={x∣ci​(x)≤0,i=1,2,⋯,m}.
对于问题（11），根据上街介绍的不等式约束的增广拉格朗日函数表达式，其增广拉格朗日函数为：
L σ ( x , λ ) = f ( x ) + σ 2 ∑ i = 1 m ( m a x { λ i σ + c i ( x ) , 0 } − λ i 2 σ 2 ) L_{\sigma}(x,\lambda)=f(x)+\frac{\sigma}{2}\sum_{i=1}^{m}(max\{\frac{\lambda_i}{\sigma}+c_i(x), 0\}-\frac{\lambda_i^2}{\sigma^2}) Lσ​(x,λ)=f(x)+2σ​i=1∑m​(max{σλi​​+ci​(x),0}−σ2λi2​​)
其中$\lambda$和$\sigma$分别为乘子以及罚因子。
给定一系列单调递增的乘子${\sigma }_k\uparrow {\sigma }_{\infty }$以及初始乘子${\lambda }_0$，问题（11）的增广拉格朗日函数法为
x k + 1 ≈ a r g min ⁡ x ∈ R n L σ k ( x , λ k ) , λ k + 1 = λ k + σ k ∇ λ L σ k ( x k + 1 , λ k ) = max ⁡ { 0 , λ k + σ k c ( x k + 1 ) } (12) \begin{aligned} &x^{k+1}\approx arg\min_{x\in R^n}L_{\sigma_k}(x,\lambda_k),\\ &\lambda^{k+1}=\lambda^k+\sigma_k\nabla_{\lambda}L_{\sigma_k}(x^{k+1},\lambda_k)=\max\{0,\lambda_k+\sigma_kc(x^{k+1})\} \end{aligned}\tag{12} ​xk+1≈argx∈Rnmin​Lσk​​(x,λk​),λk+1=λk+σk​∇λ​Lσk​​(xk+1,λk​)=max{0,λk​+σk​c(xk+1)}​(12)
为了方便叙述，一下定义${\varphi }_k(x)=L_{{\sigma }_k}(x,{\lambda }_k)$.由于${\varphi }_k(x)$的最小值点的显示表达式通常式未知的，我们往往调用迭代算法求其一个近似解。为了保证收敛性，我们要求该近似解至少满足如下非精确条件之一：
$${\varphi }_k(x^{k+1})-inf{\varphi }_k\le \frac{{ϵ}_k^2}{2{\sigma }_k},{ϵ}_k\ge 0,\sum _{k=1}^{\infty }{ϵ}_k<+\infty \text{\hspace{1em}(13)}$$
$${\varphi }_k(x^{k+1})-inf{\varphi }_k\le \frac{{\delta }_k^2}{2{\sigma }_k}||{\lambda }_{k+1}-{\lambda }_k|{|}_2^2,{\delta }_k>0,\sum _{k=1}^{\infty }{\delta }_k<+\infty \text{\hspace{1em}(14)}$$
$$dist(0,\partial {\varphi }_k(x^{k+1}))\le \frac{{\delta }_k^{{}^{\prime }}}{{\delta }_k}||{\lambda }_{k+1}-{\lambda }_k|{|}_2,0\le {\delta }_k^{{}^{\prime }}\to 0,\text{\hspace{1em}(15)}$$
其中${ϵ}_k,{\delta }_k,{\delta }_k^{{}^{\prime }}$是认为设定的参数，$dist(0,\partial {\varphi }_k(x^{k+1}))$表示0到集合$\partial {\varphi }_k(x^{k+1})$的欧几里得距离，根据${\lambda }_{k+1}$的更新格式（12）容易得知
∣ ∣ λ k + 1 − λ k ∣ ∣ 2 = ∣ ∣ m a x { 0 , λ k + σ k c ( x k + 1 ) } − λ k ∣ ∣ 2 = ∣ ∣ m a x { − λ k , σ k c ( x k + 1 ) } ∣ ∣ 2 \begin{aligned} ||\lambda_{k+1}-\lambda_k||_2 &=||max\{0,\lambda_k+\sigma_kc(x^{k+1})\}-\lambda_k||_2 \\ &=||max\{-\lambda_k,\sigma_kc(x^{k+1})\}||_2 \end{aligned} ∣∣λk+1​−λk​∣∣2​​=∣∣max{0,λk​+σk​c(xk+1)}−λk​∣∣2​=∣∣max{−λk​,σk​c(xk+1)}∣∣2​​
由于$\inf {\varphi }_k$是位置的，直接验证上述不精确条件是数值上不可行的。但是，如果${\varphi }_k$是$\alpha -$强凸函数，那么
$${\varphi }_k(x)-\inf {\varphi }_k\le \frac{1}{2\alpha }dis{t}^2(0,\partial {\varphi }_k(x))\text{\hspace{1em}(16)}$$
根据（16）式，可以进一步构造如下数值可验证的不精确条件：
$$\begin{array}{rl}& dist(0,\partial {\varphi }_k(x^{k+1}))\le \sqrt{\frac{\alpha }{{\sigma }_k}}{ϵ}_k,{ϵ}_k\ge 0,\sum _{k=1}^{\infty }{ϵ}_k<+\infty \\ & dist(0,\partial {\varphi }_k(x^{k+1}))\le \sqrt{\frac{\alpha }{{\sigma }_k}}{\delta }_k||{\lambda }_{k+1}-{\lambda }_k|{|}_2,{\delta }_k\ge 0,\sum _{k=1}^{\infty }{\delta }_k<+\infty \\ & dist(0,\partial {\varphi }_k(x^{k+1}))\le \frac{{\delta }_k^{{}^{\prime }}}{{\sigma }_k}||{\lambda }_{k+1}-{\lambda }_k|{|}_2,0\le {\delta }_k^{{}^{\prime }}\to 0.\end{array}$$

不精确条件下的增广拉格朗日函数法的收敛性证明这里省略。

四、基追踪问题的增广拉格朗日函数法
本小节以基追踪（BP）问题为例讨论增广拉格朗日函数法。我们见看到针对一些凸问题，增广拉格朗日函数法会有比较特殊的性质，比如固定罚因子也能保证算法的收敛性甚至有限终止性等。
设$A\in R^{m\times n},b\in R^m,x\in R^n$，BP问题为
$$\underset{x\in R^n}{\min }||x|{|}_1,s.t.Ax=b.\text{\hspace{1em}(17)}$$
引入拉格朗日乘子$y\in R^m$，BP问题的拉格朗日函数为
$$L(x,y)=||x|{|}_1+y^T(Ax-b)$$
那么对偶函数
KaTeX parse error: Unknown column alignment: - at position 43: … \begin{array} -̲b^Ty, &||A^Ty||…
因此我们得到如下对偶问题：
$$\underset{y\in R^m}{\min }{b}^{T}y,s.t.||A^{T}y|{|}_{\infty }\le 1\text{\hspace{1em}(18)}$$
通过引入变量$s$，上述问题可以等价地携程
$$\underset{y\in R^m,s\in R^n}{\min }{b}^{T}y,s.t.A^{T}y-s=0,||s|{|}_{\infty }\le 1\text{\hspace{1em}(19)}$$
下面讨论如何对原始问题和对偶问题应用拉格朗日函数法。

1. 原始问题的增广拉格朗日函数法
   引入罚因子$\sigma$和乘子$\lambda$，问题（17）的增广拉格朗日函数为
   $$L_{\sigma }(x,\lambda )=||x|{|}_1+{\lambda }^T(Ax-b)+\frac{\sigma }{2}||Ax-b|{|}_2^2\text{\hspace{1em}(20)}$$
   在增广拉格朗日函数法的一般理论中，需要罚因子$\sigma$足够大来保证迭代收敛。对于BP问题，可以证明，对于固定的非负罚因子也能够保证收敛性（尽管在实际中动态调整罚因子可能会使算法更快收敛）。现在考虑固定罚因子$\sigma$情形的增广拉格朗日函数法。在第$k$步迭代，更新格式为
   { x k + 1 = a r g min ⁡ x ∈ R n L σ ( x , λ k ) = a r g min ⁡ x ∈ R n { ∣ ∣ x ∣ ∣ 1 + σ 2 ∣ ∣ A x − b + λ k σ ∣ ∣ 2 2 } λ k + 1 = λ k + σ ( A x k + 1 − b ) . (21) \left\{ \begin{array}{rcl} &x^{k+1}&=arg\min_{x\in R^n}L_{\sigma}(x,\lambda_k)=arg\min_{x\in R^n}\{||x||_1+\frac{\sigma}{2}||Ax-b+\frac{\lambda_k}{\sigma}||_2^2\} \\ &\lambda_{k+1}&=\lambda_k+\sigma(Ax^{k+1}-b). \end{array} \right.\tag{21} {​xk+1λk+1​​=argminx∈Rn​Lσ​(x,λk​)=argminx∈Rn​{∣∣x∣∣1​+2σ​∣∣Ax−b+σλk​​∣∣22​}=λk​+σ(Axk+1−b).​(21)
   设迭代的初始点为$x^0={\lambda }^0=0$。考虑迭代格式（21）中的第一步，假设$x^{k+1}$为$L_{\sigma }(x,{\lambda }^k)$的一个全局极小解，那么
   $$0\in \partial ||x^{k+1}|{|}_1+\sigma A^T(A{x}^{k+1}-b+\frac{{\lambda }_k}{\sigma })$$
   因此
   $$-A^T{\lambda }_{k+1}\in \partial ||x^{k+1}|{|}_1\text{\hspace{1em}(22)}$$
   满足上式的$x^{k+1}$往往是不能显式得到的，因此需要采用迭代算法来进行求解，比如次梯度法或者近似点梯度法等等。
   这里我们沿用之前的A和b的生成方式，选取不同的稀疏度$r=0.1$和$r=0.2$。我们固定罚因子$\sigma$，并采用近似点梯度法作为求解器，不精确地求解关于$x$的子问题得到$x^{k+1}$。具体地，设置求解精度${\eta }_k=10^{-k}$，并且使用BB步长作为线搜索的初始步长，下图展示了算法产生的迭代点与最优点的举例变化以及约束违反度的走势。从图中可以看出：对于BP问题，固定的$\sigma$也可以保证增广拉格朗日函数法的收敛性

%% 基追踪问题的增广拉格朗日函数法%% 初始化和迭代准备
% 输入信息: 初始迭代点 $x^0$ 和数据 $A$, $b$，以及停机准则参数结构体 |opts| 。
%
% 输出信息: 迭代得到的解 $x$ 和包含算法求解中的相关迭代信息结构体 |out| 。
%
% * |out.feavec| ：每一步外层迭代的约束违反度 $\|Ax-b\|_2$
% * |out.inn_itr| ：总的内层迭代的步数（即近似点梯度法的迭代步数）
% * |out.tt| ：程序运行时间
% * |out.fval| ：迭代结束时的目标函数值
% * |out.itr| ：外层迭代步数
% * |out.itervec| ：迭代点列 $x$function [x, out] = BP_ALM(x0, A, b, opts)
%%%
% 从输入的结构体 |opts| 中读取参数或采取默认参数。
%
% * |opts.itr| ：外层迭代的最大迭代步数
% * |opts.itr_inn| ：内层迭代的最大迭代步数
% * |opts.sigma| ：罚因子
% * |opts.tol0| ：初始的收敛精度
% * |opts.gamma| ：线搜索参数
% * |opts.verbose| ：表示输出的详细程度， |>1| 时每一步输出， |=1| 时每一次外层循环输出， |=0| 时不输出
if ~isfield(opts, 'itr'); opts.itr = 20; end
if ~isfield(opts, 'itr_inn'); opts.itr_inn = 2500; end
if ~isfield(opts, 'sigma'); opts.sigma = 1; end
if ~isfield(opts, 'tol0'); opts.tol0 = 1e-1; end
if ~isfield(opts, 'gamma'); opts.gamma = 1; end
if ~isfield(opts, 'verbose'); opts.verbose = 2; end
sigma = opts.sigma;
gamma = opts.gamma;%%%
% 迭代准备。
k = 0;
tt = tic;
out = struct();%%%
% 计算并记录初始时刻的约束违反度。
out.feavec = norm(A*x0 - b);
x = x0;
lambda = zeros(size(b));
out.itr_inn = 0;%%%
% 记录迭代过程的优化变量 $x$ 的值。
itervec = zeros(length(x0),opts.itr);%%%
% $\sigma A^\top A$ 的最大特征值，用于估计步长。
L = sigma*eigs(A'*A,1);%% 迭代主循环
% 以 |opts.itr| 为最大迭代次数。
while k < opts.itr  Axb = A*x - b;c = Axb + lambda/sigma;g = sigma*(A'*c);tmp = .5*sigma*norm(c,2)^2;f = norm(x,1) + tmp;nrmG = norm(x - prox(x - g,1),2);tol_t = opts.tol0*10^(-k);t = 1/L;Cval = tmp; Q = 1;k1 = 0;%%%% 内层循环，当最优性条件违反度小于阈值，或者超过最大内层迭代次数限制时，退出内层循环。while k1 < opts.itr_inn && nrmG > tol_t%%%% 记录上一步的结果。gp = g;xp = x;x = prox(xp - t*gp, t);nls = 1;while 1tmp = 0.5 *sigma*norm(A*x - b + lambda/sigma, 2)^2;if tmp <= Cval + g'*(x-xp) + .5*sigma/t*norm(x-xp,2)^2 || nls == 5break;end%%%% 如果没有达到线搜索标准，衰减步长，重新试探。t = 0.2*t;nls = nls + 1;x = prox(xp - t * g, t);end%%%% 退出线搜索后，更新各量的值。f = tmp + norm(x,1);nrmG = norm(x - xp,2)/t;Axb = A*x - b;c = Axb + lambda/sigma;g = sigma*(A' * c);dx = x - xp;dg = g - gp;dxg = abs(dx'*dg);if dxg > 0if mod(k,2) == 0t = norm(dx,2)^2/dxg;elset = dxg/norm(dg,2)^2;endend%%%% 取步长为上述 BB 步长和 $1/L$中的较大者，并限制在 $10^{12}$ 范围内。t = min(max(t,1/L),1e12);%%%% 计算 (Zhang & Hager) 线搜索准则中的递推常数，其满足 $C_0=f(x^0),\ C_{k+1}=(\gamma% Q_kC_k+f(x^{k+1}))/Q_{k+1}$，序列 $Q_k$ 满足 $Q_0=1,\ Q_{k+1}=\gamma% Q_{k}+1$。Qp = Q; Q = gamma*Qp + 1; Cval = (gamma*Qp*Cval + tmp)/Q;%%%% 当需要详细输出时，输出每一步的结果，利用 |k1| 记录内层迭代的迭代步数。k1 = k1 + 1;if opts.verbose > 1fprintf('itr_inn: %d\tfval: %e\t nrmG: %e\n', k1, f,nrmG);endend%%%% 每一次内层迭代结束输出当前的结果。if opts.verbosefprintf('itr_inn: %d\tfval: %e\t nrmG: %e\n', k1, f,nrmG);end%% 更新拉格朗日乘子% 在通过近似点梯度法对 $x$ 进行更新之后，对拉格朗日乘子 $\lambda$ 进行更新，迭代格式为% $\lambda^{k+1}=\lambda^k+\sigma(Ax^{k+1}-b)$。lambda = lambda + sigma*Axb;%%%% 迭代步数加 1，依次记录外层迭代后的约束违反度、每一步迭代的 $x$ 的值，更新内层迭代的总次数。k = k + 1;out.feavec = [out.feavec; norm(Axb)];itervec(:,k) = x;out.itr_inn = out.itr_inn + k1;
end%%%
% 外层迭代结束，记录输出。
out.tt = toc(tt);
out.fval = f;
out.itr = k;
out.itervec = itervec;
end%% 辅助函数
function y = prox(x,mu)
y = max(abs(x) - mu, 0);
y = sign(x) .* y;
end

主函数

%% 构造基追踪问题
% 设定随机种子。
clear;
seed = 97006855;
ss = RandStream('mt19937ar','Seed',seed);
RandStream.setGlobalStream(ss);
%%%
% 构造基追踪问题， $u$ 为问题的真实解（其稀疏度为 $0.1$），使得 $b=Au$, $x^0$ 为随机的迭代初始点。
m = 512;
n = 1024;
A = randn(m, n);
u = sprandn(n, 1, 0.1);
b = A * u;
x0 = randn(n, 1);
%%%
% 参数设定。
opts.verbose = 0;
opts.gamma = 0.85;
opts.itr = 7;
%% 求解基追踪问题
% 调用算法 |BP_ALM| 求解 BP 问题。
[x, out] = bp_alm(x0, A, b, opts);figure
stem(u)
hold on
stem(x, 'rx')
axis tight
legend('u', 'x')

求解结果如下