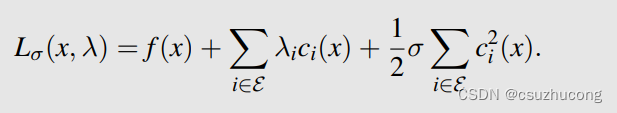增广拉格朗日函数法( Augmented Lagrangian method)
一、等式约束
考虑问题:
min x f ( x ) s . t . c i ( x ) = 0 , i = 1 , ⋯ , m . \begin{array}{ll} \min_x &f(x)\\ s.t. &c_i(x) = 0, \quad i=1,\cdots,m. \end{array} minxs.t.f(x)ci(x)=0,i=1,⋯,m.
定义增广拉格朗日函数:
L t ( x , λ ) = f ( x ) − ∑ i λ i c i ( x ) + t 2 ∑ i ( c i ( x ) ) 2 L_t(x,\lambda) = f(x) - \sum_i \lambda_ic_i(x) + \frac{t}{2}\sum_i\big(c_i(x)\big)^2 Lt(x,λ)=f(x)−i∑λici(x)+2ti∑(ci(x))2
增广拉格朗日函数可以理解为在拉格朗日函数的基础上加了一个二次惩罚项,所以该方法是拉格朗日函数法与罚函数法的结合。
求解方法类似于对偶上升法,不过梯度上升的步长改成了固定的参数 t t t,算法迭代步骤为:
- 固定 λ \lambda λ, 更新x:
x + = arg min x L t ( x ; λ ) x^+ = \argmin_x L_t(x;\lambda) x+=xargminLt(x;λ)
意味着
∇ x L t ( x + ; λ ) = ∇ f ( x + ) − ∑ i ( λ i − t c i ( x + ) ) ∇ c i ( x + ) = 0 \nabla_x L_t(x^+;\lambda) = \nabla f(x^+) - \sum_i\big( \lambda_i-tc_i(x^+)\big)\nabla c_i(x^+) = 0 ∇xLt(x+;λ)=∇f(x+)−i∑(λi−tci(x+))∇ci(x+)=0 - 更新 λ \lambda λ:
λ i + = λ i − t c i ( x + ) \lambda_i^+ = \lambda_i-tc_i(x^+) λi+=λi−tci(x+)
二、不等式约束
考虑问题:
min x f ( x ) s . t . c i ( x ) ≥ 0 , i = 1 , ⋯ , m . \begin{array}{ll} \min_x &f(x)\\ s.t. & c_i(x) \geq 0, \quad i=1,\cdots,m. \end{array} minxs.t.f(x)ci(x)≥0,i=1,⋯,m.
其等价形式为:
min x f ( x ) s . t . c i ( x ) − ν i = 0 , ν i ≥ 0 , i = 1 , ⋯ , m . \begin{array}{ll} \min_x &f(x)\\ s.t. &c_i(x) - \nu_i =0, \\ & \nu_i \geq 0,\quad i=1,\cdots,m. \end{array} minxs.t.f(x)ci(x)−νi=0,νi≥0,i=1,⋯,m.
定义带约束的增广拉格朗日函数:
L t ( x , λ ) = f ( x ) − ∑ i λ i ( c i ( x ) − ν i ( x ) ) + t 2 ∑ i ( c i ( x ) − ν i ( x ) ) 2 s . t . ν i ≥ 0 , i = 1 , ⋯ , m . L_t(x,\lambda) = f(x) - \sum_i \lambda_i \big(c_i(x)-\nu_i(x)\big) + \frac{t}{2}\sum_i\big(c_i(x)-\nu_i(x)\big)^2 \\ s.t. \quad \nu_i \geq 0,\quad i=1,\cdots,m. Lt(x,λ)=f(x)−i∑λi(ci(x)−νi(x))+2ti∑(ci(x)−νi(x))2s.t.νi≥0,i=1,⋯,m.
算法迭代步骤为:
-
固定 λ \lambda λ, 更新 x , ν x,\nu x,ν:
( x + , ν + ) = arg min x , ν L t ( x ; λ ) = arg min x , ν f ( x ) + ∑ i { − λ i ( c i ( x ) − ν i ( x ) ) + t 2 ( c i ( x ) − ν i ( x ) ) 2 } s . t . ν i ≥ 0 , i = 1 , ⋯ , m . (1) \begin{array}{rl} (x^+,\nu^+) &= \arg\min_{x,\nu} \quad L_t(x;\lambda) \\ &= \arg\min_{x,\nu}\quad f(x) + \sum_i \left\{ -\lambda_i \big(c_i(x)-\nu_i(x)\big) + \frac{t}{2}\big(c_i(x)-\nu_i(x)\big)^2 \right\} \tag{1}\\ s.t. &\quad \nu_i \geq 0,\quad i=1,\cdots,m. \end{array} (x+,ν+)s.t.=argminx,νLt(x;λ)=argminx,νf(x)+∑i{−λi(ci(x)−νi(x))+2t(ci(x)−νi(x))2}νi≥0,i=1,⋯,m.(1) -
更新 λ \lambda λ: λ i + = λ i − t ( c i ( x + ) − ν i + ) \lambda_i^+ = \lambda_i-t(c_i(x^+)-\nu_i^+) λi+=λi−t(ci(x+)−νi+)
事实上,算法中的 ν \nu ν 可以消去,由(1)式
( x + , ν + ) = arg min x , ν f ( x ) + ∑ i { − λ i ( c i ( x ) − ν i ( x ) ) + t 2 ( c i ( x ) − ν i ( x ) ) 2 } = arg min x , ν f ( x ) + t 2 ∑ i { − ( λ i t ) 2 + ( c i ( x ) − ν i ( x ) − λ i t ) 2 } = arg min x , ν f ( x ) + t 2 ∑ i { ( c i ( x ) − ν i ( x ) − λ i t ) 2 } s . t . ν i ≥ 0 , i = 1 , ⋯ , m . (2) \begin{array}{rl} (x^+,\nu^+) &= \arg\min_{x,\nu}\quad f(x) + \sum_i \left\{ -\lambda_i \big(c_i(x)-\nu_i(x)\big) + \frac{t}{2}\big(c_i(x)-\nu_i(x)\big)^2 \right\} \\ &= \arg\min_{x,\nu}\quad f(x) + \frac{t}{2}\sum_i \left\{ -(\frac{\lambda_i}{t})^2 + \big(c_i(x)-\nu_i(x) - \frac{\lambda_i}{t}\big)^2 \right\} \\ &= \arg\min_{x,\nu} \quad f(x) + \frac{t}{2}\sum_i \left\{ \big(c_i(x)-\nu_i(x) - \frac{\lambda_i}{t}\big)^2 \right\} \\ s.t. &\quad \nu_i \geq 0,\quad i=1,\cdots,m. \tag{2} \end{array} (x+,ν+)s.t.=argminx,νf(x)+∑i{−λi(ci(x)−νi(x))+2t(ci(x)−νi(x))2}=argminx,νf(x)+2t∑i{−(tλi)2+(ci(x)−νi(x)−tλi)2}=argminx,νf(x)+2t∑i{(ci(x)−νi(x)−tλi)2}νi≥0,i=1,⋯,m.(2)
从(2)式第二项很容易看出,假如先求得 x + x^+ x+,必然有
ν i + = max ( c i ( x + ) − λ i t , 0 ) \nu_i^+ = \max(c_i(x^+) - \frac{\lambda_i}{t},0) νi+=max(ci(x+)−tλi,0)
上式中取 max \max max 是为了满足 ν \nu ν 非负的约束条件。将其代回 (1) 式,得
x + = arg min x f ( x ) + ∑ i ψ ( c i ( x ) , λ i , t ) x^+ = \arg\min_x \quad f(x) + \sum_i \psi(c_i(x),\lambda_i,t) x+=argxminf(x)+i∑ψ(ci(x),λi,t)
其中
ψ ( c i ( x ) , λ i , t ) = { − λ i c i ( x ) + t 2 c i ( x ) 2 , 如果 c i ( x ) − λ i / t < 0 , − λ i 2 2 t , o t h e r w i s e . \psi(c_i(x),\lambda_i,t)=\left\{ \begin{array}{ll} -\lambda_i c_i(x) + \frac{t}{2}c_i(x)^2, & \text{如果} c_i(x) - \lambda_i/t <0, \\\\ -\frac{\lambda_i^2}{2t}, &otherwise. \end{array} \right. ψ(ci(x),λi,t)=⎩⎨⎧−λici(x)+2tci(x)2,−2tλi2,如果ci(x)−λi/t<0,otherwise.
然后更新 λ \lambda λ: λ + = max ( λ i − t c i ( x + ) , 0 ) \lambda^+ = \max(\lambda_i - tc_i(x^+),0) λ+=max(λi−tci(x+),0)