哈夫曼树的编码和解码

article/2025/8/25 9:30:44

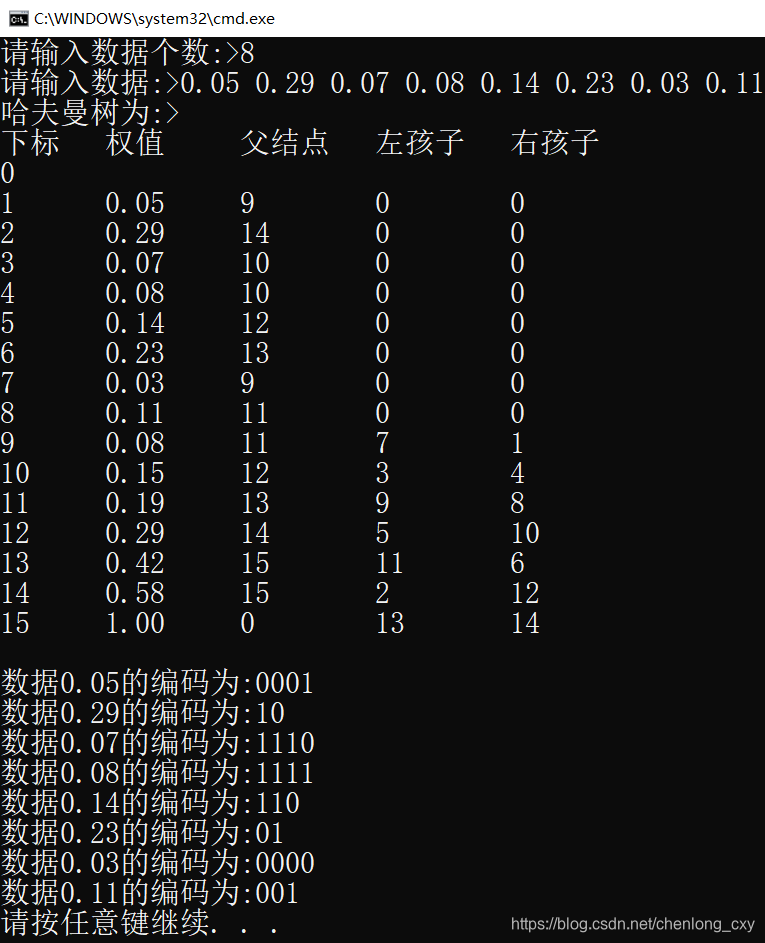
     哈夫曼树的作用：在数据通信中，需要将传送的文字转换成二进制的字符串，用0，1码的不同排列来表示字符。例如，需传送的报文为“AFTER DATA EAR ARE ART AREA”，这里用到的字符集为“A，E，R，T，F，D”，各字母出现的次数为{8，4，5，3，1，1}。现要求为这些字母设计编码。要区别6个字母，最简单的二进制编码方式是等长编码，固定采用3位二进制，可分别用000、001、010、011、100、101对“A，E，R，T，F，D”进行编码发送，当对方接收报文时再按照三位一分进行译码。显然编码的长度取决报文中不同字符的个数。若报文中可能出现26个不同字符，则固定编码长度为5。然而，传送报文时总是希望总长度尽可能短。在实际应用中，各个字符的出现频度或使用次数是不相同的，如A、B、C的使用频率远远高于X、Y、Z，自然会想到设计编码时，让使用频率高的用短码，使用频率低的用长码，以优化整个报文编码。

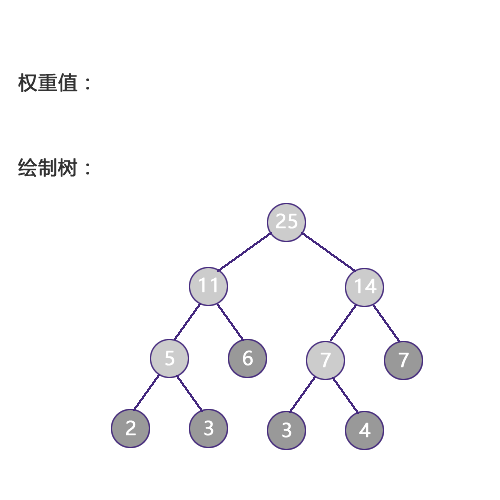
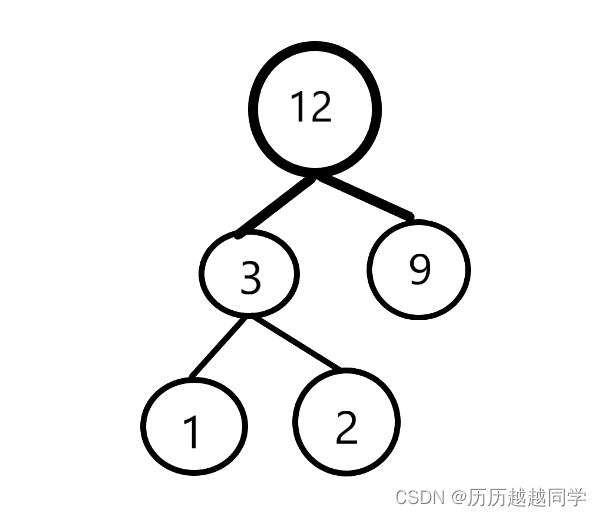
哈夫曼树的结构

//创建一个树结点
typedef struct TreeNode{char data;     //结点元素int weight;    //树的权重int parent;    //双亲结点int lchild;    //左孩子int rchild;    //右孩子
}TreeNode;    //创建一个树(顺序存储)
typedef struct HFTree{TreeNode* data;    int length;    //树的长度
}HFTree;

初始化哈夫曼树

//初始化哈夫曼树
HFTree* initTree(int* weight,int length)
{HFTree* T=(HFTree*)malloc(sizeof(HFTree));T->data=(TreeNode*)malloc(sizeof(TreeNode)*(2*length-1));T->length=length;for(int i=0;i<length;i++){T->data[i].weight=weight[i];T->data[i].parent=0;	//刚开始为空T->data[i].lchild=-1;	//刚开始为空T->data[i].rchild=-1;	//刚开始为空}for (int i = 0; i <length; i++){//scanf("%c ",&HT[i].data);char a = getchar();if(a == '\n')												//遇到回车就结束break;elseT->data[i].data = a;		//给每个结点赋予数据}return T;
}

选择权重最小的函数(便于哈夫曼树的创建)

//选择权重最小的函数
int* selectMin(HFTree* T)
{int min=10000;int secondmin=100000;int minIndex,secondminIndex;	//便于最小的两个权值无法在进行对比//找出最小的权值for(int i=0;i<T->length;i++)	{if(T->data[i].parent==0){if(T->data[i].weight<min){min=T->data[i].weight;minIndex=i; 	//便于后面求出第二小的权值}}}//求出第二小的权值for(int i=0;i<T->length;i++){if(T->data[i].parent==0&&i!=minIndex){if(T->data[i].weight<secondmin){secondmin=T->data[i].weight;secondminIndex=i;}}}int* res=(int*)malloc(sizeof(int)*2); 	//放回两个值要用指针;res[0]=minIndex;res[1]=secondminIndex;return res;   //返回res指针
}

创建哈夫曼树

//创建哈夫曼树
void createHFTree(HFTree* T)
{int* res;int min;int secondmin;int len=T->length*2-1;	//总共有2n-1个结点for(int i=T->length;i<len;i++){res=selectMin(T);min=res[0];secondmin=res[1];T->data[i].weight=T->data[min].weight+T->data[secondmin].weight;//双亲结点权重等于左右孩子权重之和T->data[i].lchild=min;T->data[i].rchild=secondmin;T->data[min].parent=i;T->data[secondmin].parent=i;T->length++;T->data[i].parent=0;}
}

 哈夫曼树的编码

​
void createHuffmanCode(HFTree* T, huffmanCode& HC, int n)
{HC = (huffmanCode)malloc(sizeof(huffmanCode) * n + 1);		/*申请len + 1个huffmanCode大小huffmanCode类型的临时空间因为下标是从一开始，所以我们要申请比结点多一个的结点，和哈夫曼树的结构对应，方便输出*/char* cd = (char*)malloc(sizeof(char) * n);		//申请n个char大小char类型的临时空间，这个临时数组记录每次遍历出来的编码int start = 0,c = 0,f = 0;				//start为cd数组记录下标，c初始为叶子结点下标，而后就是孩子结点的下标，f记录双亲结点的下标cd[n - 1] = '\0';					//这个就是给printf留着的，因为printf不会生成'\0'，如果用puts就不用这句语句了for (int i = 0; i <n; i++)		//只要叶子结点的编码{start = n - 1;					//这句要赋值n的话，start--要写在判断后方c = i;							//指向叶子结点f = T->data[c].parent;			//指向双亲结点while (f != 0)					//根结点没有双亲{start--;if (T->data[f].lchild == c)			//是左孩子就是0，右孩子就为1cd[start] = '0';elsecd[start] = '1';c = f; f = T->data[c].parent;				//向根结点接近}HC[i] = (char*)malloc(sizeof(char) * (n - start));	//给数组里的数组申请n - start个char大小的char*类型的临时空间strcpy(HC[i], &cd[start]);		//cd里记录的编码给HC的第i个数组}free(cd);				//释放临时空间
}​

 哈夫曼树的解码

void HuffmanDecoding(HFTree* T,int n,char* pwd,int Len)
{//从根结点出发，是走0左子树，1走右子树，直到遇到叶子结点，然后再从根结点出发printf("Original:");int len=strlen(pwd);	//获取用户输入编码的长度int i=0;int t=Len;		//初始化为从根结点出发while(i<len){if(pwd[i]=='0')	//是0，走左子树{t=T->data[t].lchild;i++;if(T->data[t].lchild==-1&&T->data[t].rchild==-1){printf("%c",T->data[t].data);t=Len;		//重新从根结点出发}}if(pwd[i]=='1')	//是1，走右子树{t=T->data[t].rchild;i++;if(T->data[t].lchild==-1&&T->data[t].rchild==-1){printf("%c",T->data[t].data);t=Len;}}}
}

 主函数

int main()
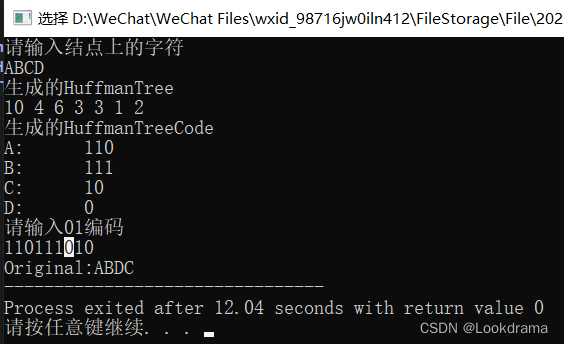
{int weight[]={1,2,3,4};int len=sizeof(weight)/sizeof(weight[0]);	//求出权值数组长度;printf("请输入结点上的字符\n");HFTree* T=initTree(weight,len);huffmanCode HC;createHFTree(T);createHuffmanCode(T,HC,len);printf("生成的HuffmanTree\n");preOrder(T,T->length-1);printf("\n生成的HuffmanTreeCode\n");for(int i=0;i<len;i++){printf("%c:\t",T->data[i].data);printf("%s\n",HC[i]);}char s[MAXSIZE];printf("请输入01编码\n");scanf("%s",s);HuffmanDecoding(T,len,s,T->length-1);return 0;
}

 完整代码

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define MAXSIZE 10000//创建一个树结点
typedef struct TreeNode{char data;int weight;int parent;int lchild;int rchild;
}TreeNode;//创建一个树(顺序存储)
typedef struct HFTree{TreeNode* data;int length;
}HFTree; typedef char** huffmanCode;	
/*第一个*是代表它是指针变量，说明它是数组;
第二个*说明它是指针数组
代表这个char类型数组里每个元素都是*huffmanCode变量*///初始化哈夫曼树
HFTree* initTree(int* weight,int length)
{HFTree* T=(HFTree*)malloc(sizeof(HFTree));T->data=(TreeNode*)malloc(sizeof(TreeNode)*(2*length-1));T->length=length;for(int i=0;i<length;i++){T->data[i].weight=weight[i];T->data[i].parent=0;	//刚开始为空T->data[i].lchild=-1;	//刚开始为空T->data[i].rchild=-1;	//刚开始为空}for (int i = 0; i <length; i++){//scanf("%c ",&HT[i].data);char a = getchar();if(a == '\n')												//遇到回车就结束break;elseT->data[i].data = a;		//给每个结点赋予数据}return T;
}//选择权重最小的函数
int* selectMin(HFTree* T)
{int min=10000;int secondmin=100000;int minIndex,secondminIndex;	//便于最小的两个权值无法在进行对比//找出最小的权值for(int i=0;i<T->length;i++)	{if(T->data[i].parent==0){if(T->data[i].weight<min){min=T->data[i].weight;minIndex=i; 	//便于后面求出第二小的权值}}}//求出第二小的权值for(int i=0;i<T->length;i++){if(T->data[i].parent==0&&i!=minIndex){if(T->data[i].weight<secondmin){secondmin=T->data[i].weight;secondminIndex=i;}}}int* res=(int*)malloc(sizeof(int)*2); 	//放回两个值要用指针;res[0]=minIndex;res[1]=secondminIndex;return res;
}//创建哈夫曼树
void createHFTree(HFTree* T)
{int* res;int min;int secondmin;int len=T->length*2-1;	//总共有2n-1个结点for(int i=T->length;i<len;i++){res=selectMin(T);min=res[0];secondmin=res[1];T->data[i].weight=T->data[min].weight+T->data[secondmin].weight;//双亲结点权重等于左右孩子权重之和T->data[i].lchild=min;T->data[i].rchild=secondmin;T->data[min].parent=i;T->data[secondmin].parent=i;T->length++;T->data[i].parent=0;}
}//前序遍历哈夫曼树
void preOrder(HFTree* T,int index)	//index为data数组中的索引
{if(index!=-1){printf("%d ",T->data[index].weight);preOrder(T,T->data[index].lchild);preOrder(T,T->data[index].rchild);}
}void createHuffmanCode(HFTree* T, huffmanCode& HC, int n)
{HC = (huffmanCode)malloc(sizeof(huffmanCode) * n + 1);		/*申请len + 1个huffmanCode大小huffmanCode类型的临时空间因为下标是从一开始，所以我们要申请比结点多一个的结点，和哈夫曼树的结构对应，方便输出*/char* cd = (char*)malloc(sizeof(char) * n);		//申请n个char大小char类型的临时空间，这个临时数组记录每次遍历出来的编码int start = 0,c = 0,f = 0;				//start为cd数组记录下标，c初始为叶子结点下标，而后就是孩子结点的下标，f记录双亲结点的下标cd[n - 1] = '\0';					//这个就是给printf留着的，因为printf不会生成'\0'，如果用puts就不用这句语句了for (int i = 0; i <n; i++)		//只要叶子结点的编码{start = n - 1;					//这句要赋值n的话，start--要写在判断后方c = i;							//指向叶子结点f = T->data[c].parent;			//指向双亲结点while (f != 0)					//根结点没有双亲{start--;if (T->data[f].lchild == c)			//是左孩子就是0，右孩子就为1cd[start] = '0';elsecd[start] = '1';c = f; f = T->data[c].parent;				//向根结点接近}HC[i] = (char*)malloc(sizeof(char) * (n - start));	//给数组里的数组申请n - start个char大小的char*类型的临时空间strcpy(HC[i], &cd[start]);		//cd里记录的编码给HC的第i个数组}free(cd);				//释放临时空间
}void HuffmanDecoding(HFTree* T,int n,char* pwd,int Len)
{//从根结点出发，是走0左子树，1走右子树，直到遇到叶子结点，然后再从根结点出发printf("Original:");int len=strlen(pwd);	//获取用户输入编码的长度int i=0;int t=Len;		//初始化为从根结点出发while(i<len){if(pwd[i]=='0')	//是0，走左子树{t=T->data[t].lchild;i++;if(T->data[t].lchild==-1&&T->data[t].rchild==-1){printf("%c",T->data[t].data);t=Len;		//重新从根结点出发}}if(pwd[i]=='1')	//是1，走右子树{t=T->data[t].rchild;i++;if(T->data[t].lchild==-1&&T->data[t].rchild==-1){printf("%c",T->data[t].data);t=Len;}}}
}
int main()
{int weight[]={1,2,3,4};int len=sizeof(weight)/sizeof(weight[0]);	//求出权值数组长度;printf("请输入结点上的字符\n");HFTree* T=initTree(weight,len);huffmanCode HC;createHFTree(T);createHuffmanCode(T,HC,len);printf("生成的HuffmanTree\n");preOrder(T,T->length-1);printf("\n生成的HuffmanTreeCode\n");for(int i=0;i<len;i++){printf("%c:\t",T->data[i].data);printf("%s\n",HC[i]);}char s[MAXSIZE];printf("请输入01编码\n");scanf("%s",s);HuffmanDecoding(T,len,s,T->length-1);return 0;
}

 编译的结果

 

 


http://chatgpt.dhexx.cn/article/b2W9RLG0.shtml

相关文章

哈夫曼树与哈夫曼编码

哈夫曼树与哈夫曼编码

哈夫曼树 给定n个权值作为n个叶子结点&#xff0c;构造一棵二叉树&#xff0c;若带权路径长度达到最小&#xff0c;称这样的二叉树为最优二叉树&#xff0c;也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树&#xff0c;权值较大的结点离根较近。 树节点间的边…
阅读更多...
【例题】哈夫曼树

【例题】哈夫曼树

【例1】由五个分别带权值为9&#xff0c;2&#xff0c;3&#xff0c;5&#xff0c;14的叶子结点构成的一棵哈夫曼树&#xff0c;该树的带权路径长度为_______________。 A、60 B、66 C、67 D、50 答案&#xff1a;C 解析&#xff1a; 关键点在于要学会如何构造哈夫曼树 已知有5…
阅读更多...
哈夫曼树以及哈夫曼算法

哈夫曼树以及哈夫曼算法

目录 一、哈夫曼树的定义 二、哈夫曼树的特点 三、哈夫曼算法(构造哈夫曼树的方法) 四、哈夫曼树的构造过程 五、哈夫曼树构造算法的实现 一、哈夫曼树的定义 1、哈夫曼树:最优树即带权路径长度(WPL)最短的树 “带权路径长度最短”是在"度相同”的树中比较而得的结果…
阅读更多...
哈夫曼树的绘制

哈夫曼树的绘制

数据结构之哈夫曼树绘制 本人还是一个年轻的程序猿(还是个学生)&#xff0c;请大家多多指教&#xff01; 哈夫曼树 已知权重绘制哈夫曼树 开始我的表演 Step 1. 已知权重&#xff1a;2&#xff0c;3&#xff0c;3&#xff0c;4&#xff0c;7&#xff0c;6 Step 2. 选取其中…
阅读更多...
哈夫曼树 哈夫曼编码

哈夫曼树 哈夫曼编码

哈夫曼树 哈夫曼树的定义&#xff1a;设二叉树具有 n 个带权值的叶节点&#xff0c;那么从根节点到各个叶节点的路径长度与相应叶节点权值的乘积的和&#xff0c;叫作二叉树的带权路径长度 WPL (Weighted Path Length)。具有最小带权路径长度的二叉树称为哈夫曼树 (Huffman Tr…
阅读更多...
哈夫曼树(Huffman Tree)

哈夫曼树(Huffman Tree)

定义 哈夫曼树又称最优二叉树&#xff0c;是一种带权路径长度最短的二叉树。所谓树的带权路径长度&#xff0c;就是树中所有的叶结点的权值乘上其到根结点的路径长度&#xff08;若根结点为0层&#xff0c;叶结点到根结点的路径长度为叶结点的层数&#xff09;。树的路径长度是…
阅读更多...
哈夫曼树详解

哈夫曼树详解

一、哈夫曼树的介绍 Huffman Tree&#xff0c;中文名是哈夫曼树或霍夫曼树&#xff0c;它是最优二叉树。 定义&#xff1a;给定n个权值作为n个叶子结点&#xff0c;构造一棵二叉树&#xff0c;若树的带权路径长度达到最小&#xff0c;则这棵树被称为哈夫曼树。 这个定义里面涉…
阅读更多...
哈夫曼树(Huffmantree)

哈夫曼树(Huffmantree)

1.基本概念 哈夫曼树又称为最优树&#xff0c;是一类带权路径长度最短的树。 一些概念的定义&#xff1a; &#xff08;1&#xff09;路径&#xff1a;树的两个结点之间的连线称为路径。 &#xff08;2&#xff09;路径长度&#xff1a;路径上的分支数目称作路径长度。若规定…
阅读更多...
哈夫曼树详解及其应用(哈夫曼编码）

哈夫曼树详解及其应用(哈夫曼编码）

一&#xff0c;哈夫曼树的基本概念 路径&#xff1a;从树中一个结点到另一个结点之间的分支构成这两个结点间的路径 结点的路径长度&#xff1a;两结点之间路径上的分支数 树的路径长度&#xff1a;从树根到每一个结点的路径长度之和&#xff0e;记作&#xff1a;&#xff3…
阅读更多...
哈夫曼树编码的实现+图解（含全部代码）

哈夫曼树编码的实现+图解（含全部代码）

目录 哈夫曼树的基本概念 ------------哈夫曼树的构造方法 ------------------------哈夫曼编码 ------------------------------------全部代码 哈夫曼树的基本概念 哈夫曼树通常以二叉树的形式出现&#xff0c;所以也称最优二叉树&#xff0c;是一类带权路径长度最短的树…
阅读更多...
哈夫曼树（C语言实现）

哈夫曼树（C语言实现）

文章目录 哈夫曼树的基本概念哈夫曼树的构建构建思路代码实现 哈夫曼编码的生成编码生成思路代码实现 完整代码展示以及代码测试 哈夫曼树的基本概念 在认识哈夫曼树之前&#xff0c;你必须知道以下几个基本术语&#xff1a; 1、什么是路径&#xff1f; 在一棵树中&#xff0c…
阅读更多...
打开VS2010提示：产品密钥框

打开VS2010提示：产品密钥框

打开VS2010提示&#xff1a;产品密钥框&#xff0c;如下图&#xff1a; …
阅读更多...
VS 2017 产品密钥

VS 2017 产品密钥

个人分类&#xff1a; vs2010 Visual Studio 2017&#xff08;VS2017&#xff09; 企业版 Enterprise 注册码&#xff1a;NJVYC-BMHX2-G77MM-4XJMR-6Q8QF Visual Studio 2017&#xff08;VS2017&#xff09; 专业版 Professional 激活码key&#xff1a;KBJFW-NXHK6-W4WJM-CRM…
阅读更多...
vs++2010学习版的注册密钥

vs++2010学习版的注册密钥

6VPJ7-H3CXH-HBTPT-X4T74-3YVY7 欢迎使用Markdown编辑器 你好&#xff01; 这是你第一次使用 Markdown编辑器 所展示的欢迎页。如果你想学习如何使用Markdown编辑器, 可以仔细阅读这篇文章&#xff0c;了解一下Markdown的基本语法知识。 新的改变 我们对Markdown编辑器进行…
阅读更多...
存储过程入门

存储过程入门

参考文章 Oracle Database concepts guide&#xff08;11g2&#xff09; By Thomas KyteStored Procedure Wiki 先修知识 数据库的基本概念SQL 什么是存储过程&#xff08;Stored Procedure&#xff09;&#xff1a; 一段存储在数据库的“子程序”&#xff0c;下面对这两个…
阅读更多...
【MySQL存储过程】创建一个简单的存储过程

【MySQL存储过程】创建一个简单的存储过程

什么是存储过程和函数 存储过程和函数是在数据库中定义的一些SQL语句的集合&#xff0c;然后直接调用这些存储过程和函数来执行已经定义好的SQL语句。存储过程和函数可以避免开发人员重复编写相同的SQL语句。而且&#xff0c;存储过程和函数是在MySQL服务器中存储和执行的&…
阅读更多...
什么是存储过程

什么是存储过程

什么是存储过程&#xff1a;存储过程可以说是一个记录集吧&#xff0c;它是由一些T-SQL语句组成的代码块&#xff0c;这些T-SQL语句代码像一个方法一样实现一些功能&#xff08;对单表或多表的增删改查&#xff09;&#xff0c;然后再给这个代码块取一个名字&#xff0c;在用到…
阅读更多...
MySQL-存储过程

MySQL-存储过程

文章目录 存储过程一. 存储过程的创建和使用1. 创建存储过程2. 删除存储过程3. 查看存储过程4. 调用存储过程5. 例题 二. 变量1. 系统变量1.1 全局变量1.2 会话变量 2. 自定义变量2.1 用户变量2.2 局部变量 三. 存储过程参数3.1 说明&#xff1a;3.2 例题 四. 流程控制1. IF语句…
阅读更多...
存储过程怎么使用

存储过程怎么使用

1.什么是存储过程&#xff1f; 存储过程是封装了一条或多条SQL的集合。它的好处是简单、高性能、安全。2.为什么要使用存储过程&#xff1f; 简化复杂的操作&#xff0c;把SQL封装起来容易使用。 如果所有开发人员和应用程序都使用同一存储过程&#xff0c;则所有使用的代码都…
阅读更多...
SQL创建存储过程

SQL创建存储过程

创建SQL存储过程需要使用到的语法 - 创建存储过程 CREATE 存储过程的名称(参数) BEGIN ...需要执行的SQL语句 END- 调用 CALL 存储过程的名称(参数)个人看法&#xff0c;这就是一个函数...无参数 CREATE PROCEDURE p_student_select() BEGIN SELECT * FROM student; ENDCALL …
阅读更多...
推荐文章

Copyright @ 2022~2023