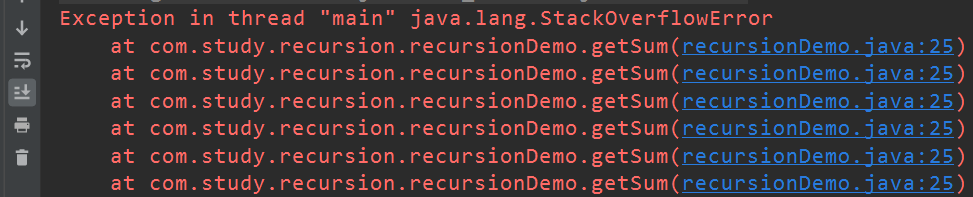
1.递归的概念：

一个方法在执行过程中调用自身, 就称为 "递归".

示例：

//递归求n的阶乘
public static void main(String[] args) {int n = 5;int ret = factor(n);System.out.println("ret = " + ret);
}public static int factor(int n) {if (n == 1) {return 1;}return n * factor(n - 1);
}

2.递归执行过程分析

示例：

//递归求n的阶乘 加上日志
public static void main(String[] args) {int n = 5;int ret = factor(n);System.out.println("ret = " + ret);
}public static int factor(int n) {System.out.println("函数开始, n = " + n);if (n == 1) {System.out.println("函数结束, n = 1 ret = 1");return 1;}int ret = n * factor(n - 1);System.out.println("函数结束, n = " + n + " ret = " + ret);return ret;
}

//结果

函数开始, n = 5
函数开始, n = 4
函数开始, n = 3
函数开始, n = 2
函数开始, n = 1
函数结束, n = 1 ret = 1
函数结束, n = 2 ret = 2
函数结束, n = 3 ret = 6
函数结束, n = 4 ret = 24
函数结束, n = 5 ret = 120
ret = 120

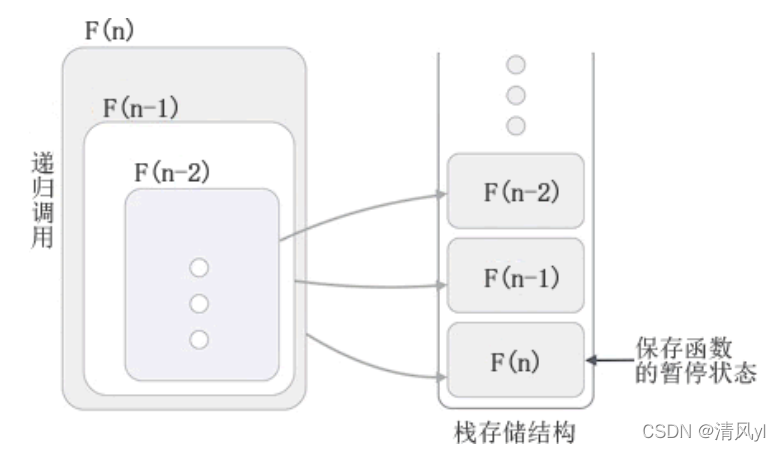
执行过程图：

 

程序按照序号中标识的 (1) -> (8) 的顺序执行

3.递归练习

示例1：

//按顺序打印一个数字的每一位（例如 1234 打印出 1 2 3 4）

public static void print(int num) {if (num > 9) {print(num / 10);}System.out.println(num % 10);
}

示例2：

//递归求 1+2+3+...+10
public static int sum(int num) {if (num == 1) {return 1;}return num + sum(num - 1);
}

示例3：

//写一个递归方法,输入一个非负整数，返回组成它的数字之和，例如，输入1729，则返回

//1+7+2+9

public static int sum(int num) {if (num < 10) {return num;}return num % 10 + sum(num / 10);
}

示例4：求斐波那契数列的第N项

public static int fib(int n) {if (n == 1 || n == 2) {return 1;}return fib(n - 1) + fib(n - 2);
}

当我们求fib(40)的时候发现，程序执行速度极慢，原因是进行了大量的重复运算。

public class Test {public static int count = 0;public static void main(String[] args) {System.out.println(fib(40));System.out.println(count);}public static int fib(int n) {if (n == 1 || n == 2) {return 1;}if (n == 3) {count++;}return fib(n - 1) + fib(n - 2);}
}

可以使用循环的方式来求斐波那契数列问题, 避免出现冗余运算

public static int fib(int n) {int last2 = 1;int last1 = 1;int cur = 0;for (int i = 3; i <= n; i++) {cur = last1 + last2;last2 = last1;last1 = cur;}return cur;
}

此时程序的执行效率大大提高了.

小结：

递归是一种重要的编程解决问题的方式.

有些问题天然就是使用递归方式定义的(例如斐波那契数列, 二叉树等), 此时使用递归来解就很容易.

有些问题使用递归和使用非递归(循环)都可以解决. 那么此时更推荐使用循环, 相比于递归, 非递归程序更加高效.